 |
Главная |
II. Теоретическая часть инерционных колебаний на подводных трубопроводах
|
из
5.00
|
Колеблющийся подводный трубопровод имеет длину, значительно превышающую его диаметр (при меньшей длине колебания трубопроводов не происходят), максимальная амплитуда колебании также значительно меньше его длины. Поэтому можно считать, что при колебаниях угол между осью трубы и нормалью к ней практически мало отличается от 90°. Очевидно, в этом случае величины присоединенной массы для жесткого цилиндра и упругоколеблющегося трубопровода такого же диаметра должны различаться незначительно, т. е. результаты экспериментов. полученные п условиях плоской задачи, можно использовать применительно к трубопроводам, представляющим собой пространственную конструкцию. Это предположение подтверждается результатами экспериментов, выполненных авторами с жесткими и упругими моделями цилиндров.
Следует отметить, что при определении собственных частот высших тонов изгибных колебаний стержней и соответствующих им значений присоединенной массы жидкости необходимо учитывать деформацию сдвига и инерцию поворота сечения. При неучете этих факторов величина присоединенной массы жидкости будет зависеть от номера гармоники колебаний, что и имело место во многих ранее выполненных исследованиях.
Таким образом, присоединенная масса жидкости для колеблющегося трубопровода в безграничной жидкости принимается как и для жесткого тела по формуле
 (1)
(1)
где р —плотность жидкости; D и l — внешний диаметр и длина трубопровода.
При колебаниях подводных трубопроводов могут быть самые разнообразные граничные условия (расположение трубопровода на дне, вблизи дна и свободной поверхности, в траншее), затрудняющие теоретическое определение присоединенной массы жидкости. Поэтому для установления инерционного влияния окружающей воды на колебания подводного трубопровода авторами были выполнены экспериментальные исследования применительно к различным условиям практики.
Существуют различные экспериментальные методы определения присоединенной массы. В приводимых исследованиях присоединенную массу определяли сравнением частот вертикальных колебаний цилиндра в воздухе и в жидкости. Основное достоинство этого метода — простота установки и получение достоверных данных, так как опыты проводятся в реальной жидкости с учетом реальных граничных условий.
Опыты проводили в гидравлическом лотке прямоугольного сечения размером 1X1, 5x12 м в условиях плоской и пространственной задач. Для случая плоской задачи применяли жесткие цилиндры диаметрами D=28,5108 мм, длиной L около 1000 мм. Для случая пространственной задачи использовали модели цилиндров размерами D = 32/1 мм, L=4481 мм; D=33/2 мм, L — 2894 мм; D=51/1,4 мм и L=5400 мм. Цилиндры по концам закреплялись шарнирно и представляли собой систему с распределенными параметрами, собственные колебания их соответствовали первому тону. Частоту и амплитуду колебаний измеряли тензорезисторами с использованием усилителя ТА-5 и осциллографа Н700.
Опыты проводились для следующих безразмерных параметров: относительное расстояние от свободной поверхности до верха образующей цилиндра h/D=0; 0,25; 0,5; 1,0; 1,5; 2.0; 3,0 и 4.0; относительное расстояние от дна лотка до нижней образующей цилиндра s/D=0.25; 0.5; 0,75; 1.0; 1,5; 2.0; 2,5; 3.0 и 4.0.
При колебаниях трубопроводов в траншеях исследовалось влияние на присоединенную массу следующих параметров: относительное удаление трубопровода от дна s/D = 0,25; 0.5; 1,0; 1,5; 2,0; угол заложения откосов траншеи а = 0; 45; 60 и 90°; относительная ширина траншеи но дну b/D = 2; 3; 4 и 5.
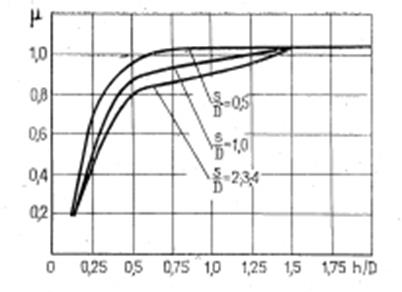
Результаты экспериментов представлены на графике (рис. 1) зависимости коэффициента присоединенной массы р (отношение присоединенной массы mпр к массе жидкости, заключенной в объеме цилиндра mv, т. е. μ= mпр/mv) от положения, занимаемого цилиндром относительно дна s/D и свободной поверхности h/D. Как видно из графика, коэффициент присоединенной массы повышается с уменьшением s/D и снижается с уменьшением h/D. При удалении цилиндра на расстояние около 3D и более от дна и свободной поверхности коэффициент присоединенной массы практически остается постоянным и не зависит от s/D и h/D. Снижение μ с уменьшением h/D<3D объясняется снижением инерционного воздействия окружающей трубопровод поды и появлением волновой составляющей гидродинамического давления, которая сдвинута относительно перемещения трубопровода по фазе на π/2 и играет роль «присоединенного трения».
При частичном погружении цилиндра в воду (например, в случае укладки трубопровода свободным погружением или расположении трубопровода на плаву) расчетная схема его соответствует балке на нелинейном упругом основании, и частоты колебаний трубопровода значительно уменьшаются вследствие влияния упругости основания.
Для расчетов колебаний подводных трубопроводов применительно к различным условиям практики величину присоединенной массы следует определять по формуле
mпр = μmv (2)
Значение коэффициента присоединенной массы μ принимается в зависимости от расположения трубопровода относительно дна и свободной поверхности потока или траншеи но графикам рис. 1.
|
из
5.00
|
Обсуждение в статье: II. Теоретическая часть инерционных колебаний на подводных трубопроводах |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

