 |
Главная |
Срок представления к защите ______________________________
|
из
5.00
|
Заведующий кафедрой ______________ В.И. Халимон .
(подпись, дата) (инициалы, фамилия)
Лектор, ____________________ ____________________
должность (подпись, дата ) (инициалы, фамилия)
Руководитель, ____________________ ____________________
должность (подпись, дата ) (инициалы, фамилия)
Задание принял ____________________ Е. А. Потехин
к выполнению (подпись, дата ) (инициалы, фамилия)
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. АНАЛИЗ МЕТОДОВ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
1.1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЛИНЕЙНОЙ ЗАВИСИМОСТИ ИЗ ГРАФИКА
После нанесения на график экспериментальных точек по ним «на глаз» проводят прямую. Строят ее таким образом, чтобы точки в среднем одинаково располагались по обе стороны от прямой. На рис.1 это прямая 1-2. На ней выбирают две точки (1 и 2)максимально удаленные друг от друга.
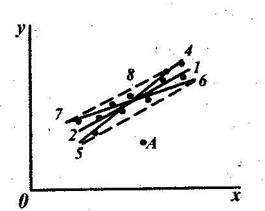
Рис.1 Графическая обработка линейной зависимости.
Их координаты х1, y1 и х2, y2 подставляют в (1) для получения двух уравнений с неизвестными а и b:
y1=ax1+b;
y2=ax2+b,
из которых находят:
 ,
,  (2)
(2)
Для оценивания ∆а и ∆b строят две дополнительные прямые симметричные относительно прямой 1-2, чтобы экспериментальные точки, в основном, располагались между ними.
Если на графике имеются точки, которые отстоят от основной прямой 1-2 более, чем на утроенное среднее расстояние точек до прямой (это хорошо заметно уже при рассматривании графика - на рис.1 такой точкой является точка А), то их отбрасывают и не используют при построении дополнительных прямых. Соответствующие измерения, скорее всего, содержат промахи.
Дополнительные прямые определяют «коридор погрешностей» эксперимента, внутри которого находится исследуемая линейная зависимость. Предельные случаи хода этой зависимости получатся, если провести прямые через противоположные углы «коридора» (прямые 4-5 и 6-7). Тем же способом, что и для основной прямой 1-2, находят параметры предельных прямых ai, bi и а2, b2. Оценки погрешностей:
 ,
, 
Может оказаться, что теоретическую зависимость между измеряемыми величинами предполагают линейной, а экспериментальные точки явно не ложатся на прямую. Проведение по ним прямой, как это сделано на рис 2, неправомерно. Расхождение между теоретической н экспериментальной зависимостями свидетельствует о наличии систематических погрешностей, которые должны быть выявлены и учтены при обработке результатов. Иначе экспериментатору остается только констатировать расхождение модели с экспериментом.

Рнс.2 Пример необоснованной интерпретации экспериментальной зависимости как линейной.
Часто линейная зависимость является приближенно справедливой в ограниченном интервале изменения физических величин. В таком случае необходимо определить границы применимости линейной зависимости и указать их при анализе результатов эксперимента.
1.2. МЕТОД ПАРНЫХ ТОЧЕК
В некоторых экспериментах основной интерес представляет только угловой коэффициент зависимости (1). Для оценивания значения коэффициента и определения его погрешности удобен метод парных точек. Он заключается в следующем.
После нанесения на график экспериментальных точек из них выбирают пары, в которых точки отстоят друг от друга примерно на одинаковое расстояние. Желательно, чтобы это расстояние было максимально возможным. Через каждую пару проводят прямую, а затем согласно (2) вычисляют угловые коэффициенты всех прямых. Из получившегося набора коэффициентов по правилам обработки данных прямых измерении определяют среднее значение коэффициента и его погрешность. Их принимают за результат измерения искомого параметра зависимости (1).
Например, конкретной обработка данных эксперимента по измерению сопротивления R участка электрической цепи. Даны измеренные значения тока I и соответствующие им значения падения напряжения U.
Теоретическое описание исследуемой зависимости дает закон Ома:
U = R·I,
где сопротивление R является угловым коэффициентом линейной зависимости, проходящей через начало координат. Значит, для его определения можно воспользоваться методом парных точек. Проставляют экспериментальные точки на график (рис 3) и нумеруют их по порядку от 1 до 8. Выбирают пары точек 1-5, 2-6, 3-7, 4-8 и заносят их координаты в табл. 1, которую используют для проведения необходимых вычислений.

Рис.3 Зависимость падения напряжения от тока в цепи.
Таблица 1. Обработка данных методом парных точек
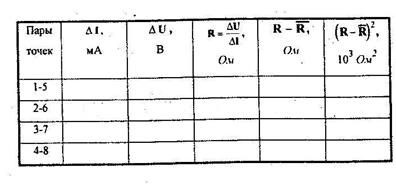
Вычисляют среднее значение сопротивления:
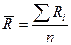 .
.
Далее переходят к вычислению дисперсии:
 .
.
Для n и доверительной вероятности α находят табличный коэффициент Стьюдента, и домножением на него дисперсии получают 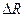 . Окончательный результат:
. Окончательный результат:
 .
.
Точность измерения сопротивления невелика, что свидетельствует о наличии значительных экспериментальных погрешностей
2. ОПИСАНИЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин яруг от друга. В том числе, он применим к линейной зависимости и позволяет получить достоверные оценки ее параметров а и b, а также оценить их погрешности.
Пусть имеется установка, работающая по принципу «черного ящика». На входе в данную установку мы можем установить вектор входных параметров xi, а на выходе из установки измерить вектор выходных параметров yi, где i=1..n. Число n представляет собой число опытов (рис. 4).

Рис. 4 Изображение исследуемого объекта.
Существование зависимости между двумя наборами величин xi, и yi, где i=1..n можно определить с помощью коэффициента парной корреляции rxy, численная величина которого вычисляется по формуле:
 (3)
(3)
Коэффициент парной корреляции находится в пределах -1≤ rxy ≤+1, то есть  или
или 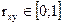 . Чем ближе коэффициент парной корреляции находится к единице, тем сильнее зависимость yi=f(xi). При равенстве коэффициента парной корреляции нулю зависимость отсутствует. По числовому значению коэффициента парной корреляции можно сделать предположение о виде зависимости.
. Чем ближе коэффициент парной корреляции находится к единице, тем сильнее зависимость yi=f(xi). При равенстве коэффициента парной корреляции нулю зависимость отсутствует. По числовому значению коэффициента парной корреляции можно сделать предположение о виде зависимости.
Если коэффициент парной корреляции по абсолютной величине равен единице, то существует линейная зависимость yi=a·xi+b (рис. 5).

Рис. 5 Вид линейной зависимости
Если коэффициент парной корреляции положительный, то с увеличением аргумента, увеличивается значение функции (рис. 6).
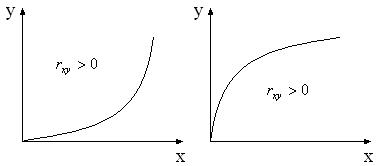
Рис. 6 С увеличением аргумента увеличивается значение функции
При отрицательном коэффициенте парной корреляции с увеличением аргумента, уменьшается значение функции (рис. 7).

Рис. 7 – С увеличением аргумента уменьшается значение функции
В случае существования зависимости между входными и выходными параметрами объекта исследования ищется уравнение регрессии. Для поиска уравнения регрессии используется метод наименьших квадратов.
Суть метода наименьших квадратов заключается в следующем. Предполагается, что зависимость между величинами является линейной: yi=a·xi+b и сумма квадратов отклонений расчетных значений от экспериментальных - должна быть минимальной.
Расчетное значение запишем в следующем виде:
 (4)
(4)
Сумму квадратов отклонений расчетных значений от экспериментальных запишем в виде:
 (5)
(5)
В выражение (5) подставим уравнение регрессии (4) и получим:
 (6)
(6)
Известно, что экстремум функции достигается тогда, когда первая производная равна нулю. В нашем случае имеются два неизвестных: a и b. По данным коэффициентам возьмем две частные производные:
 (7)
(7)
Разделим оба уравнение системы (5) на -2. В результате, раскрыв скобки, получим систему из двух линейных уравнений с двумя неизвестными a и b:
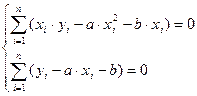 ;
; 
 (8)
(8)
Данная система может быть решена с помощью метода Крамера. Главный определитель системы ∆ равен:

Коэффициенты при неизвестном a и b заменяем столбцом свободных членов, получаем определители:
 и
и

Вычисляем коэффициенты по правилу Крамера:
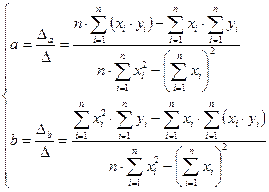 (9)
(9)
Таким образом, получены коэффициенты уравнения регрессии ypi=a·xi+b.
Уравнение регрессии (4) может адекватно описывать процесс только в интервале экспериментальных значений, с помощью которых вычислялись коэффициенты уравнения регрессии:
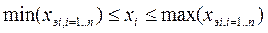 .
.
Для оценки адекватности модели, на практике могут быть использованы следующие оценки: корреляционное отношение η и средняя относительная ошибка ε:
 , (10)
, (10)
где  - среднее значение выходного параметра.
- среднее значение выходного параметра.
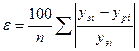 (11)
(11)
В настоящее время существует ряд нелинейных зависимостей, которые могут быть приведены к линейному виду yi=a·xi+b. Операция приведения нелинейной зависимости к линейному виду называется линеаризацией.
Вариант 10. Определить начальную скорость счета I0 и период полураспада T1/2 радиоактивного элемента по зависимости скорости счета от времени:
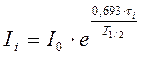 ,
,  (12)
(12)
Приведем нелинейное уравнение (12) к линейному виду. Прологарифмируем обе части уравнения:

Проведем замену переменных:
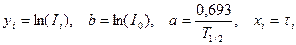 ,
,
в результате получим уравнение yi=b+a·xi или yi=a·xi+b.
Таким образом, для того, чтобы найти предэкспоненциальный множитель - начальную скорость счета I0 и период полураспада T1/2 радиоактивного элемента, необходимо проделать следующие действия:
1. yi=ln(Ii), xi=τi;
2. 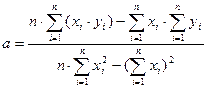 ,
, 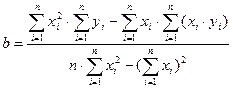 (13)
(13)
Кроме этого, следует вычислить среднеквадратические ошибки a и b.
Находим дисперсию:
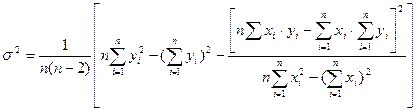 (14)
(14)
Далее находим дисперсию параметра a:
 (15)
(15)
После этого находим дисперсию параметра b:
 (16)
(16)
Согласно ГОСТ Р 8.736 доверительная вероятность P=0,95. При такой вероятности P и количестве измерений n=7 количество степеней свободы f=6, значит коэффициент Стьюдента (таблица) равен t=2,44691184879, тогда домножив дисперсии параметров a и b на коэффициент Стьюдента найдем абсолютные ошибки для a и b.
a=a±σa·t
b=b±σb·t
3. I0=eb, T1/2=0,693/а (17)
4.  .
.
Следует отметить, что погрешность метода наименьших квадратов в полтора раза меньше, чем у метода парных точек.
ПРАКТИЧЕСКАЯ ЧАСТЬ
1.1. БЛОК-СХЕМА ПРОГРАММНОГО КОМПЛЕКСА
Для программы Microsoft Visual Studio:
 | |||
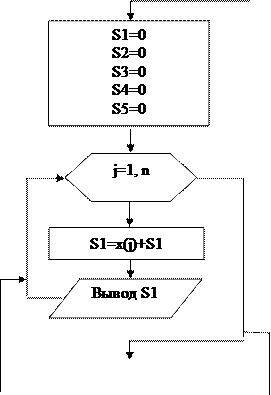 |

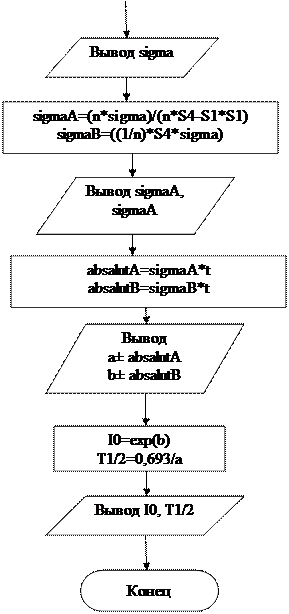
Для программы Microsoft Excel:
 |
1.2. ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЯ ПРОГРАММНОГО КОМПЛЕКСА
Для программы Microsoft Visual Studio:
1) Вводим количество экспериментальных данных n
2) Вводим экспериментальные данные τ и I
3) Нажимаем кнопку построить график
4) Получаем таблицу расчетных данных, искомые a, b,  и
и  , а также построенные графики функций I(τ) и Iрi(τ)
, а также построенные графики функций I(τ) и Iрi(τ)
Для программы Microsoft Excel:
1) Записываем экспериментальные τ и I данные в таблицу
2) Строим график функции I(τ) и линию тренда

3) Создаем расчетные ячейки относительно экспериментальных данных, а именно, присваиваем xi=τi, yi=Ln(Ii)
4) Делаем вспомогательные расчеты: xi· xi; xi·yi и yi· yi
5) Вычисляем суммы всех расчетных данных:  ,
,  ,
,  ,
, 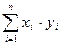 ,
, 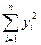
6) Получаем следующую таблицу:
| № | τ, ч | I, имп./мин. | х, ч | y | х*х | х*y | y*y |
| 7,77 | 38,85 | 60,38 | |||||
| 7,50 | 75,01 | 56,27 | |||||
| 7,24 | 108,56 | 52,38 | |||||
| 6,97 | 139,32 | 48,53 | |||||
| 6,70 | 167,39 | 44,83 | |||||
| 6,16 | 215,72 | 37,99 | |||||
| 5,62 | 252,92 | 31,59 | |||||
| сумма | 47,95 | 997,77 | 331,96 |
7) Находим по формулам (13) a и b
8) Находим дисперсии σ2,  ,
,  по формулам (14), (15),(16)
по формулам (14), (15),(16)
9) Находим абсолютные ошибки для a и b
10) Находим значение коэффициентов регрессии  и
и  по формулам (17)
по формулам (17)
11) Строим график функции Iрi(τ)

1.3. СКРИНШОТЫ РАБОЧЕЙ ПРОГРАММЫ ПО ВАРИАНТУ № 10
|
из
5.00
|
Обсуждение в статье: Срок представления к защите ______________________________ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

