Метод наименьших квадратов

Приложения

1. Значения коэффициентов Стьюдента

 

	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999
	1,000 0,816 0,765 0,741	1,376 1,061 0,978 0,941	1,963 1,336 1,250 1,190	3,08 1,886 1,638 1,533	6,31 2,92 2,35 2,13	12,71 4,30 3,18 2,77	31,8 6,96 4,54 3,75	63,7 9,92 5,84 4,60	636,6 31,6 12,94 8,61
	0,727 0,718 0,711 0,706 0,703	0,920 0,906 0,896 0,889 0,883	1,156 1,134 1,119 1,108 1,100	1,476 1,440 1,415 1,397 1,383	2,02 1,943 1,895 1,860 1,833	2.57 2,45 2,36 2,31 2,26	3,36 3,14 3,00 2,90 2,82	4,03 3,71 3,50 3,36 3,25	6,86 5,96 5,40 5,04 4,78
	0,700 0,697 0,695 0,694 0,692	0,879 0,876 0,873 0,870 0,868	1,093 1,088 1,083 1,079 1,076	1,372 1,363 1,356 1,350 1,345	1,812 1,796 1,782 1,771 1,761	2,23 2,20 2,18 2,16 2,14	2,76 2,72 2,68 2,65 2,62	3,17 3,11 3,06 3,01 2,98	4,59 4,49 4,32 4,22 4,14
∞	0,691 0,690 0,689 0,688 0,688 0,674	0,866 0,865 0,863 0,862 0,861 0,842	1,074 1,071 1,069 1,067 1,066 1,036	1,341 1,337 1,333 1,330 1,328 1,282	1,753 1,746 1,740 1,734 1,729 1,645	2,13 2,12 2,11 2,10 2,09 1,960	2,60 2,58 2,57 2,55 2,54 2,33	2,95 2,92 2,90 2,88 2,86 2,58	4,07 4,02 3,96 3,92 3,88 3,29
	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999

Здесь – доверительная вероятность; 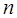– количество опытов.

 

Обработка результатов измерений

 

 

Прямые измерения

 

Прямые измерения позволяют непосредственно, при помощи прибо-ров, получить значение интересующей величины. В этом случае резуль-тат измерений представляется в следующем виде:

 

, (П.1)

 

где – среднее значение измеренной величины;

– абсолютная ошибка измерений.

Величина абсолютной ошибки определяется следующим образом:

 

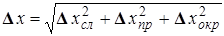, (П.2)

 

где – случайная абсолютная погрешность (иногда ее называют по-лушириной доверительного интервала);

– систематическая ошибка измерительного прибора;

– абсолютная погрешность округления.

Как правило, в лабораторном практикуме << , .

Если случайный разброс измеряемой величины отсутствует, то оста-ется только погрешность округления , приближенно равная поло-вине наименьшего значения, измеряемого прибором. Для приборов со шкалами это цена деления шкалы. При работе с табличными величи-нами в качестве погрешности округления берется половина цены млад-шего разряда величины.

Например, если дается значение сопротивления , то ошибка округления составляет , т.е. число записано с точностью до .

При наличии только случайных погрешностей результат измерений будет записан в виде

 

. (П.3)

 

При этом рассчитывается следующим образом:

 

, (П.4)

 

где – число опытов;

– коэффициент Стьюдента, величина которого зависит от и доверительной вероятности . Здесь – вероятность того, что мате-матическое ожидание величины (среднее значение при бесконечном числе измерений) окажется внутри интервала , где – среднее значение величины при данном (сделанном Вами) количестве измерений. Для работ в физическом практикуме рекомендуется брать значения или . Таблица значений коэффициентов Стью-дента приведены в Приложении 1.

Замечание. При прямых измерениях времени (ручным секундоме-ром) возникает ошибка, связанная с запаздыванием человеческой реак-ции. При этом ошибка прибора .

После вычисления величины абсолютной ошибки необходимо рас-считать относительную ошибку измерения величины :

 

. (П.5)

Косвенные измерения

 

Косвенные измерения позволяют рассчитывать интересующие нас величины по результатам прямых измерений. При этом измеряемая ве-личина является известной функцией от величин , получаемых из прямых измерений. Результат косвенного из-мерения вычисляют, подставляя в формулу для вычисления средние значения :

 

. (П.6)

 

При косвенных измерениях абсолютная ошибка величины опреде-ляется по формуле

 

, (П.7)

 

где , ,…, 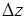- абсолютные ошибки .

В некоторых случаях формулу (П.7) можно упростить.

1. Если , то относительная ошибка величины будет в раз больше относительной ошибки :

 

. (П.8)

 

2. Если или , то относительная ошибка величины может быть рассчитана как

 

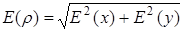, (П.9)

 

где и – относительные ошибки величин и .

 

 

Совместные измерения.

Метод наименьших квадратов

 

Если в работе одновременно измеряются величины и и пред-полагается, что они зависят друг от друга линейно:

 

,

 

то можно вычислить коэффициенты и , при которых сумма квад-ратов отклонений экспериментальных точек 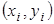от прямой линии будет минимальна (отсюда и название метода).

Коэффициенты и вычисляются следующим образом:

 

, (П.10)

 

. (П.11)

 

Здесь угловые скобки означают средние значения.

Абсолютная ошибка вычисления коэффициента :

 

, (П.12)

 

где

 

. (П.13)

 

Аналогично вычисляется абсолютная ошибка вычисления коэффи-циента :

 

, (П.14)

 

где

 

. (П.15)

 

Здесь – число экспериментальных точек.

 

 

Запись результатов

 

Представив результат в виде (П.1), не забудьте округлить его до нужной точности, т.е. до старшей значащей цифры в величине абсолют-ной ошибки.

Например, запись неверна, надо округлить до сотых:

 

.

 

Записи или неудобны для чтения; их лучше представить в виде

 

и .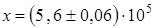
3. Вычисление производной от функции

Графическим способом

Пример приближенного расчета производной в некоторой точке кривой показан на рис. П.1.

Для расчета производной берем экспериментальную точку 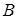, ближайшую к экспериментальной точке . Измеряем катет и катет , затем берем отношение этих катетов . Так поступаем для каждой экспериментальной точки. За-метим, что в данном примере , , поэтому знак произ-водной отрицателен. Если надо получить значение модуля произ-водной, то берем модуль полученного значения . Так получаем значения модуля производной для каждого измерения, т.е. для каждой экспериментальной точки главной кривой.

4. Плотность воздуха в зависимости от