Проверка гипотез и погрешности

Оптимизация технологической схемы

Таблица 3.1

Данные для расчета

Диаметр, мм	масса, т	выход, %	суммарный выход, %
итого

Рис 3.1 Технологическая схема

Находим массы второго и третьего продукта по формулам:

Q₃=Q₁∙E∙

Q₂=Q₁-Q₃

B1-3	Q1,т/ч	E	Q2,т/ч	Q3,т/ч
0,4		0,8

Рассчитываем массы и суммарный выход 3 продукта:

Таблица 3.2

Диаметр,мм	масса,т	выход,%	суммарный выход,%
		1,47	1,47
		5,88	7,35
		2,94	10,29
		8,82	19,11
		10,29	29,41
		4,41	33,82
		13,23	47,05
		11,76	58,82
		41,17
итого

Приравниваем массу третьего продукта Q₃=400, тогда характеристики будут выглядеть так:

 

Таблица 3.3

Диаметр,мм	Масса,т	Выход,%	Суммарный выход
		1,5	1,5
			7,5
			10,5
			19,5
		10,5
		4,5	34,5
		13,5
итого

 

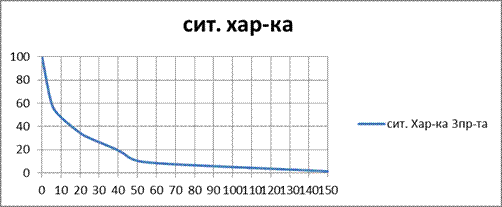
Находим массы 4го и 5го продуктов

Q3	Q4	B3-25	E	Q5
		0,7	0,6

Находим β₃ каждой крупности

B3-50	В3+30	В3-40	В3+50	В3+40	В3-20	В3+20	B3-32	B3+32
0,9	0,28	0,8	0,1	0,2	0,69	0,31	0,75	0,25
В3-10	В3-5	В3-30	В3+25	В3-24	В3-16	В3-8	В3-4
0,52	0,45	0,73	0,3	0,69	0,63	0,5	0,37

 

Находим 6й продукт после дробилки, если коэффициент закрупнения =1,7, а размер

щели =30мм:

доли щели	суммарный выход,%	диаметр,мм
0,1
0,2
0,4
0,6
0,8

 

Находим β₆ каждой крупности

В6-50	В6-40	В6-20	В6-10	В6-5	В6-30
0,95	0,89	0,6	0,34	0,2	0,78

Находим 7й продукт по формулам:

Если d<i = + ∙b^-d

Если d>i = + 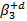∙b^-d

диаметр	суммарный выход	выход	масса
	0,5	14,5
	2,2	1,7	6,8
	5,16	2,96	11,84
	14,2	9,04	36,16
	38,48	24,28	97,12
	49,4	10,92	43,68
		50,6	202,4

Находим массы и выходы 8го, 9го и 10 го продукта:

Q7	Q9+Q8	Q10	Q8	Q9
	313,2	86,8	98,658	214,542
γ7		γ10	γ8	γ9
		21,7	24,6645	53,6355

 

Находим 10й продукт

диаметр	масса	выход	суммарный выход
		66,82	66,82
	6,8	7,83	74,65
	11,84	13,64	88,29
	10,16	11,70
	86,8

Находим 11й продукт после дробилки, если коэффициент закрупнения=2,7

а размер щели=10мм

Доли макс куска	Диаметр,мм	Суммарный выход,%	Выход,%	Масса,т
				33,40
0,1	2,2			44,53
0,2	4,4			55,67
0,4	8,8			40,08
0,6	13,2			26,72
0,8	17,6			4,45
				17,81
				222,699

Пересчет на стандартные размеры

Диаметр	суммарный	выход	масса
			16,41
			45,59
			47,42
			72,95
			182,39

Рассчитываем массы 12го, 13го и 14го продуктов

Q12	γ	β12-10
222,69	0,55	1,99
Q13	Q14
182,39	40,30

Находим 9й продукт

Диаметр,мм	Масса	Выход,%	Суммарный выход,%
	36,16	16,85	16,85
	97,12	45,26	62,12
	43,68	20,35	82,48
	37,582	17,51
итого	214,542

Находим 13й продукт

Диаметр,мм	Масса	Выход,%	Суммарный выход,%
	16,41
	45,59
	47,42
	72,95
итого	182,39

Находим 15й продукт

	Q15	396,9325
Диаметр,мм	сумма	Выход	Суммарный выход,%	масса
	25,85	12,92	12,92	51,31
	70,26	35,13	48,06	139,45
	46,35	23,17	71,24	92,00
	57,51	28,75		114,15
				396,93

 

 

Находим массы и выход 16го, 17го и 18 го продуктов

Q16	Q17	γ17
64,30	332,62	0,83
Q18	γ18
162,96	0,40

Задание для оптимизации: минимизировать класс -3, т.е минимизировать выход 18го продукта.

Для решения поставленной задачи нужно принять за исходные данные размер щели дробилки КСД1750 минимальный, т.е. 60мм и размер щели дробилки КМД1750

равным 15 мм

Аналогично пересчитать продукты:

6й продукт

доли щели	суммарный выход,%	диаметр,мм
0,1
0,2
0,4
0,6
0,8

 

 

B6-60	B6-48	В6-36	В6-24	В6-12	В6-6
0,95	0,9	0,78	0,6	0,35	0,2

7й продукт

диаметр	суммарный выход	выход	масса
	2,5	1,5
	7,6	5,1	20,4
		11,4	45,6
	39,5	20,5
		17,5

 

 

Находим массы и выходы 8го, 9го и 10 го продукта:

Q7	Q9+Q8	Q10	Q8	Q9
			12,15	257,85
γ7		γ10	γ8	γ9
		32,5	3,04	64,46

10й продукт

диаметр	масса	выход	суммарный выход
		4,60	4,61
		6,91	11,52
	20,4	23,50	35,02
	99,6	64,98	95,85
	γ10

 

 

 

11й продукт

Доли макс куска	Диаметр,мм	Суммарный выход,%	Выход,%	Масса,т
				33,40
0,1	1,5			44,53
0,2				55,67
0,4				40,08
0,6				26,72
0,8				4,45
				17,81
				222,7

 

Рассчитываем массы 12го, 13го и 14го продуктов

Q12	γ	β12-10
219,71	0,55	2,02
Q13	Q14
197,74	21,97

9й продукт

Диаметр,мм	Масса	Выход,%	Суммарный выход,%
		16,78	16,78
		38,22
		32,63	87,63
	69,85	32,56	120,19
итого	257,85

 

 

13й продукт

Диаметр,мм	Масса	Выход,%	Суммарный выход,%
	2,2	1,11	1,11
	6,66	3,37	4,48
	188,88	95,52
итого	197,74

15й продукт

	Q15	455,59
Диаметр,мм	сумма	Выход	Суммарный выход,%	масса
	16,978	8,39	8,39	38,22
	39,33	19,67	28,06	89,6
			46,05
	195,52	97,76		445,38
				445,59

 

Q16	Q17	γ17
123,01	332,58	0,83
Q18	γ18
135,16	0,17

Выход 18го продукта снизился с 41% до 17%. Таким образом, регулируя размер щели дробилок можно регулировать выход конечных продуктов, ограничиваясь минимально возможным и максимально возможным размером щели данной дробилки.

Проверка гипотез и погрешности

Задание 2.1.1 Выявить промахи, определить среднюю массовую долю,дисперсию и доверительные интервалы для среднего и частных значений. Массовая доля компонента в продукте обогащения по результатам анализа равна β_i , i=1,1.

Решение

Находим среднее арифметическое значение , дисперсию(S²) и среднеквадратичное отклонение(S), затем доверительный интервал для частных значений (x_i±S) и доверительный интервал для среднего значения ( ±S), затем выявляем промахи, для этого проверяем, входит ли значения в доверительный интервал для среднего значения. Если x_i не входит в доверительный интервал, то это значение является промахом. Если в значениях выявлены промахи, то их исключают а оставшиеся значения пересчитывают повторно, так повторяют до тех пор пока в значения не окажется ни одного промаха.

Таблица 2.1

Исходные данные:
Номер анализа
Значения	25,10	29,45	21,47	34,64	26,48	23,61	28,14	26,14	29,48	24,78
Промахи			Промах	Промах
	ТтттапвапрарапрТ
Средняя массовая доля	26,93
Дисперсия	13,71
Средне квадратичное отклонение	3,70
Доверительный интевал для среднего значения	23,23	< Xист <	30,63
Доверительный интевал для частного значения		21,40	< X1 <	28,80
	25,75	< X2 <	33,15
	17,77	< X3 <	25,17
	30,94	< X4 <	30,18
	22,78	< X5 <	30,18
	19,91	< X6 <	27,31
	24,44	< X7 <	31,84
	22,44	< X8 <	29,84
	25,78	< X9 <	33,18
	21,08	< X10 <	28,48

Таблица 2.3

Номер анализа
Значение	25,10	29,45	26,48	23,61	28,14	26,14	29,48	24,78
Промахи

Таблица 2.4

Средняя массовая доля	26,65
Дисперсия	4,79
Средне квадратичное отклонение	2,19
Доверительный интервал для среднего значения	21,86	< Хист <	31,43

Задание 2.1.2 Найти погрешность воспроизводимости для извлечения, рассчитываемого по формуле:

ε = ,

где γ-выход продукта, %; β- массовая доля ценного компонента в продукте, %; α- массовая доля ценного компонента в исходном продукте, %

Известны значения γ , β, α и их погрешности воспроизводимости Sвγ, Sвβ , Sвα. Коэффициент корреляции между показателями отсутствует.

Решение

Погрешность воспроизводимости определяется из закона сложения ошибок, а именно дисперсия:

S_вε²=(dε/dα)²∙S_вα²+(dε/dβ)²∙S_вβ²+(dε/dγ)²∙S_вγ²+(d²ε/dαdγ)∙S_вα∙S_вγ+(d²ε/dαdβ)∙S_вβ∙S_вα+

+(d²ε/dγdβ)∙S_вγ∙S_вβ

Погрешносность воспроизводимости для извлечения S= ²

Таблица 2.5

γ	45,2
β	12,9
α	6,3
Sву	0,2
Sвβ	0,17
Sва	0,16
dε/dα	-14,69
dε/dγ	2,05
dε/dβ	7,17
d²ε/dα*dγ	-0,33
d²ε/dα*dβ	-1,14
d²ε/dβ*dγ	0,16
S²(γ)	2043,04
S²(β)	166,41
S²(ε)=	44971,2

 

Задание 2.1.3 По данным 10 опытов получены результаты (ε_к) испытания нового реагента (Н. р.) в сравнении со стары реагентом (С. р.). Определить, значимо ли в среднем различие результатов при использовании нового и старого реагентов

Решение:

Сначала проверяем гипотезу о равенстве дисперсий по критерию Фишера, для этого находим дисперсии для нового и старого реагента находим расчетный критерий Фишера (S₂²/S₁²) и сравниваем его с табличным значением, расчетный меньше табличного значит гипотеза верна. Проверяем гипотезу о равенстве среднеарифметических значений по критерию Стьюдента, для этого находим среднеарифметические значения для нового и старого реагента находим расчетный критерий Стьюдента (t= 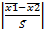∙ ). Расчетный критерий сравниваем с табличным значением, расчетное меньше табличного значит гипотеза верна. Это значит что различие в результатах использования нового и стараго реагента незначительно.

Таблица 2.6

Н.р	55,18	12,29	56,63	47,18	66,9	57,89	32,05	25,89	10,58	10,26
С.р	52,07	10,24	53,6	45,67	62,07	54,19	30,17	26,47	8,91	10,98

X₁=	37,49
X₂=	35,44
St=	1,83
S₁²=	479,90
S₂²=	424,12
F=	0,88
Fкр=	3,18

S²=	452,01
S=	21,26
t=	0,22
с=	0,53
V=	3,43
	4,00
tкр=	2,13

Задание 2.1.4 Известны результаты анализа двух проб и средние квадратические погрешности, определенные по сериям опытов (n₁ и n₂).Определить, значимо ли различаются между собой погрешности результатов опытов.

Решение

Расчет ведется аналогично заданию 2.1.3 с той лишь разницей что среднее арифметическое и дисперсии уже даны. Гипотеза о равенстве дисперсий потверждается, т.к. расчетный критерий Фишера меньше чем табличный, но гипотеза о равентсве среднеарифметических значений отвергается, т.к. расчетный критерий Стьюдента больше чем табличный. Значит различие между погрешностями результатов опытов значимо.

 

Таблица 2.6

y₁	32,08
y₂	33,07
Sy₁	0,29
Sy₂	0,22
n₁
n₂

 

S₁²=	0,08
S₂²=	0,05
F=	0,58
S²ср=	0,25
t=	6,82
ν=
tкр=	4,5

 

Задание 2.1.5 Оцените, значимы ли различия между предсказанными теоретически (т) и полученными практически (э) результатами.

Решение

Полностью аналогично задаче 2.1.3. Различия между предсказанными теоретически и полученными практически результатами не значительны

Таблица 2.7

э
т

 

 

X₁=	45,1
X₂=	36,7
St=	1,83
S₁²=	382,99
S₂²=	222,01
F=	0,58

 

S²=	302,5
S=	17,39
t=	1,08
c=	0,63
V=	16,81
	17,00
tкр=	1,74