 |
Главная |
Решение системы линейных уравнений по формулам Крамера
|
из
5.00
|
Метод обратной матрицы
Для решения системы линейных уравнений в MS Excel в рабочий лист следует ввести все данные, относящиеся к этой задаче: матрицу коэффициентов системы (т.е. матрицу А), а также вектор со значениями правых частей уравнений (вектор В). Такая таблица с внесенными в нее данными показана на рис. 1.

Рис. 1.
Прежде чем приступать к вычислениям, необходимо присвоить ячейкам и диапазонам имена.
Присвоим диапазону В5:D7 имя А(рис. 2).

Рис. 2.
Выделим диапазон ячеек B10:B12и присвоим ему имя В(рис. 3).

Рис. 3.

Теперь определяем обратную матрицу. С этой целью выделяем диапазон G5:I7, после чего в строку формул вводим формулу =МОБР(А) (рис.4).
Рис. 4.
Для того чтобы была применима именно к диапазону ячеек, необходимо нажать комбинацию клавиш Ctrl+Syift+Enter.В результате получим матрицу, обратную кА (рис. 5).

Рис. 5.
Присвоим этой матрицы имя Аобр.
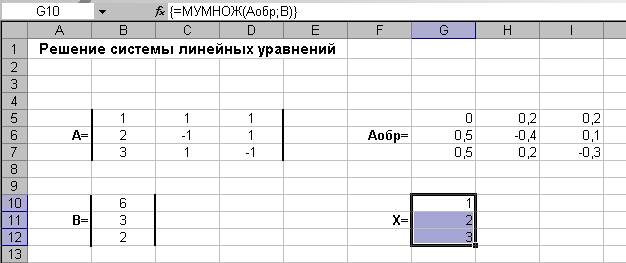
После этого осталось только найти произведение обратной матрицы Аобр и вектора, который задан массивом В. Выделяем диапазон G10:G12,присваиваем ему имя Х и вводим в строку формул выражение =МУМНОЖ(Аобр;В). После этого следует нажать Ctrl+Syift+Enter(рис. 6).
Рис. 6.
В результате проделанных вычислений получаем вектор Х, элементы которого записаны в ячейки диапазона G10:G12 и определяют последовательно значения: X1 (ячейка G10), X2 (ячейка G11), X3 (ячейка G12).
Решение системы линейных уравнений по формулам Крамера
В ячейку G6 введем формулу {=МОПРЕД(А)} для вычисления определителя матрицы А.(рис. 7).

Рис. 7.
Далее предстоит создать три новых матрицы, для которых затем будут вычисляться определители, а по этим определителям уже непосредственно отыскиваются решения системы уравнений.
Начнем с определения значения переменной Х1. Этой переменной соответствует первый столбец в матрице А коэффициентов, который должен быть заменен вектом-столбцом В (В10:В12), а два других ее столбца должны совпадать с соответствующими столбцами матрицы А. Саму матрицу А1 будем создавать в два этапа. Сначала выделяем диапазон ячеек В15:В17 и в строке формул вводим =В (рис. 8).
После нажатия комбинации клавиш Ctrl+Syift+Enterданный диапазон будет содержать в точности те же значения, что ячейки массива В. Теперь нужно заполнить два оставшихся столбца. Выделяем ячейки в диапазоне C15:D17 и присваиваем в качестве значения этому диапазону =C5:D7. Этот диапазон соответствует второму и третьему столбцам матрицы А (рис. 9).

Рис. 8.

Рис. 9.
После выполнения указанных операций в диапазоне ячеек B15:D17будет находиться именно та матрица, по детерминанту которой можно определить значение переменной Х1. Для этого в ячейку G7 вводим формулу =МОПРЕД(B15:D17)/G6 (рис. 10).

Рис. 10.
Определение значения двух других переменных (Х2, Х3) происходит также. Принципиальное различие при поиске значения переменной Х2 состоит в том, что построение вспомогательной матрицы А2происходит не в два, а в три этапа. Это связано с тем что матрица А2 получается из базовой матрицы А заменой второго, т.е. среднего столбца, на вектор-столбец В, поэтому для первого и третьего столбцов нужно выполнять присваивание отдельно (их нельзя объединять в один диапазон) (рис. 11).
Конечный результат представлен на рис. 12.


Рис. 11.
Рис. 12.
|
из
5.00
|
Обсуждение в статье: Решение системы линейных уравнений по формулам Крамера |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

