Список крупнейших банков России по размеру уставного фонда (на 1. 03.2000 г., млн. руб.)

Задача № 1

1. Построить ряды распределения по 30 коммерческим банкам РФ:

а) по величине капитала;

б) по возрасту.

По полученным рядам распределения определить среднее, модальное и медианное значение каждого показателя.

Для графического изображения изучаемых вариационных рядов построить гистограмму распределения (для интервального ряда) и полигон распределения (для дискретного ряда), а также кумулятивные кривые для изображения ряда накопленных частот.

Таблица 1

Список крупнейших банков России по размеру уставного фонда (на 1. 03.2000 г., млн. руб.)

№	Наименование	№ регистрации	Возраст	Активы-нетто	Уставный фонд	Текущая прибыль	Капитал
	Абсолют банк			49,55	7,86	0,11	9,53
	Инкасбанк			66,86	7,61	0,08	9,49
	Нижегородпром -стройбанк			89,52	7,61	2,00	25,63
	Московский кредитный			68,04	7,53	0,69	19,05
	Моск. Банкирский Дом			23,69	5,93	0,14	6,12
	Газбанк			83,80	5,79	0,51	10,14
	Красбанк			10,77	4,89	0,04	4,95
	ВТ-Банк			9,34	4,74	0,06	4,83
	Возрождение			322,42	3,88	3,16	17,23
	Московск. Индустриальн.			191,08	3,84	2,12	30,98
	Балтонэксим			102,61	3,73	0,39	7,28
	ОАО КБ Центр-Инвест			19,90	3,12	0,09	3,40
	АКБ Мосуралбанк			7,31	2,97	0,01	3,59
	Кредит-Москва			19,27	2,44	0,03	4,83
	НДБ-Банк			33,37	2,13	0,57	3,38
	Леспромбанк			8,38	2,10	0,01	2,43
	Москомприват-банк			39,82	2,02	0,21	4,86
	Огни Москвы			22,59	1,75	0,33	3,31
	Нефтеэнерго-банк			5,03	1,59	0,01	1,57
	Донской народный			5,55	1,52	0,03	1,57
	Мосфильмбанк			1,68	1,43	0,01	1,46
	Корвет			2,81	1,40	0,01	1,51
	Метрополь			21,84	1,39	0,07	2,63
	Алмаззолото			7,38	1,26	0,02	1,72
	Дзержинский			9,82	1,26	0,02	1,50
	Капиталъ-экспресс			4,26	1,26	0,01	1,64
	ИНГ Банк			313,36	1,22	9,82	43,17
	Оптбанк			4,61	1,22	0,07	1,36
	Межрегиональн. Почтовый			3,32	1,20	0,00	1,21
	Курганпромбанк			2,33	1,15	0,02	1,49

 

Решение:

а) Построим ряд распределения банков по величине капитала:

Определим число групп:

n=1+3,322lgN=1+3,322*lg30=6

Величина интервала:

Таблица 2

№ группы	Группы банков по величине капитала, млн.руб.	Чис-ло банков, fi	Сере-дина интер-вала xi	xi * fi	Сумма накоп-ленных частот, S	xi –	|xi - | * fi	(xi – )2	(xi – )2 *fi
	1,21-8,20		4,705	103,51		-4,430	97,460	19,62	431,748
	8,20-15,20		11,700	35,10		2,565	7,695	6,58	19,738
	15,20-22,19		18,695	37,39		9,560	19,120	91,39	182,787
	22,19-29,18		25,685	25,69		16,550	16,550	273,90	273,903
	29,18-36,18		32,680	32,68		23,545	23,545	554,37	554,367
	36,18-43,17		39,675	39,68		30,540	30,540	932,69	932,692
	ВСЕГО			274,05			194,910		2395,235

1. Среднее значение показателя рассчитывается как средняя арифметическая интервального ряда по формуле:

,

где x_i – середины интервалов; f_i –частота i-го интервала.

2. Мода - значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.

Модальным интервалом является 1-й интервал с частотой f_МО = 22.

где X_MO – нижняя граница модального интервала; i_MO – величина модального интервала; f_MO, f_MO-1, f_MO+1 – частоты модального, предмодального и послемодального интервалов соответственно.

3.Медиана – это варианта, которая находится в середине вариационного ряда.

Находим номер медианы: N=

Медианный интервал находится в пределах 15,20-22,19.

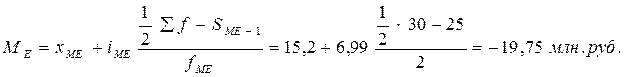
где x_ME и i- нижняя граница и величина медианного интервала; Σf – сумма частот; S _ME-1 – сумма накопленных частот, предшествующих медианному интервалу; f_ME – частота медианного интервала.

Рис. 3. Гистограмма ряда распределения банков по величине капитала

 

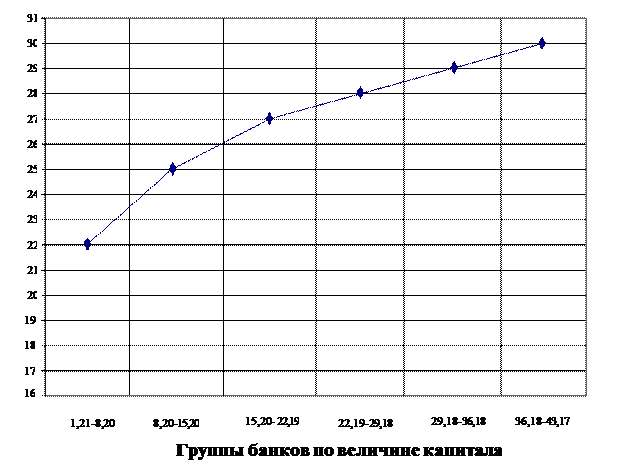
Рис. 4. Кумулята распределения

 

б) Построим ряд распределения банков по возрасту.

Величина интервала: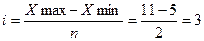

Таблица 3
№ группы	Группы банков по возрасту, лет	Число банков, fi	Середина интервала xi	xi * fi	Сумма накопленных частот, S	xi –	|xi - | * fi	(xi – )2	(xi – )2 *fi
	[5-8]		6,5	149,5		-0,7	16,1	0,49	11,27
	[8-11]		9,5	66,5		2,3	16,1	5,29	37,03
	ВСЕГО		-	216,0	-	-	32,2	-	48,30

1. Среднее значение показателя рассчитывается как средняя арифметическая интервального ряда по формуле:

где x_i – середины интервалов; f_i –частота i-го интервала.

2. Мода - значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.

Модальным интервалом является интервал 5-8 с частотой f_МО=23.

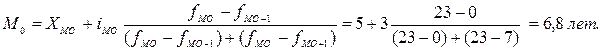
где X_MO – нижняя граница модального интервала; i_MO – величина модального интервала; f_MO, f_MO-1, f_MO+1 – частоты модального, предмодального и послемодального интервалов соответственно.

3.Медиана – это варианта, которая находится в середине вариационного ряда.

Находим номер медианы: N=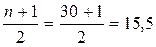

Медианный интервал находится в пределах 5-8.

где x_ME и i- нижняя граница и величина медианного интервала; Σf – сумма частот; S _ME-1 – сумма накопленных частот, предшествующих медианному интервалу; f_ME – частота медианного интервала.

Рисунок 5. Распределение банков по возрасту

 

Рисунок 6. Кумулята распределения

2. По построенным в задаче 1 рядам распределения рассчитать:

а) размах вариации;

б) среднее линейное отклонение;

в) среднее квадратичное отклонение;

г) коэффициент вариации.

Проанализировать полученные результаты.

Решение:

Для расчета показателей вариации используем расчетные данные, представленные в таблицах 2 и 3.

1) Размах вариации представляет собой абсолютную разность между максимальным и минимальным значениями признака в изучаемой совокупности:

а) R = x_max – x_min = 43,17 – 1,21 = 41,96 млн. руб.

б) R = x_max – x_min = 11 – 5 = 6 лет

2) Среднее линейное отклонение:

а)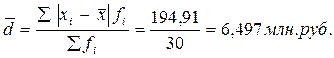

б)

3) Дисперсия:

а)

б)

4) Среднее квадратичное отклонение вычисляется как корень квадратный из дисперсии:

а)

б)

5) Коэффициент вариации – это относительный показатель вариации, равный процентному отношению среднего квадратического отклонения к средней арифметической:

а)

б)

Вывод: рассчитанная величина коэффициента вариации для распределения банков по величине капитала свидетельствует о значительном уровне колебаний признака (т.к. рассчитанный коэффициент имеет значение значительно более 33%). Данная совокупность считается неоднородной. Коэффициент вариации для распределения банков по возрастам не превышает 33 %. Данная совокупность является однородной.

Задача № 2

 

По данным задачи 1 провести 20-процентную механическую выборку банков по величине капитала. Результаты представить в таблице.

Установить:

а) средний размер капитала банков по выборке;

б) величину ошибки при определении величины капитала на основе выборки;

в) вероятные пределы колебания величины капитала для всех банков при вероятности 0,954.

Решение:

Таблица 8

№ группы	Группы банков по величине капитала, млн. руб.	Число банков, fi	Середина интервала xi	xi * fi	Сумма накопленных частот, S	xi –	|xi - | * fi	(xi – )2	(xi – )2 *fi
	8,20-15,20		11,700	11,70		-12,820	12,820	164,352	164,352
	15,20-22,19		18,695	37,39		-5,825	11,650	33,931	67,862
	22,19-29,18		25,685	25,69		1,165	1,165	1,357	1,357
	29,18-36,18		32,680	32,68		8,160	8,160	66,586	66,586
	36,18-43,17		39,675	39,68		15,155	15,155	229,674	229,674
	ВСЕГО		-	147,14	-	-	48,950	-	529,831

 

 

а) Средний размер капитала банка по выборке:

б) Средняя ошибка выборки:

μ_х = ,

где n - число единиц выборки (n = 30*0,2 = 6); N- число единиц генеральной совокупности, N = 30.

Дисперсия :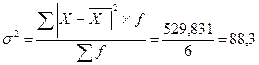

μ_х = =

Предельная ошибка выборки:

при заданной вероятности р = 0,954 коэффициент доверия t = 2

в) Вероятные пределы колебания величины капитала:

 

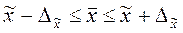
Задача № 3

Для изучения связи между активами-нетто и объёмом капитала по 30 коммерческим банкам (согласно варианту):

а) изобразите связь между изучаемыми признаками графическим построением поля корреляции;

б) постройте уравнение регрессии. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические значения объёма кредитных вложений и нанесите их на построенный график.

 

Таблица 1

Список крупнейших банков России по размеру собственного капитала
(на 1 сентября 2000 года, млн. руб.)

№	Наименование	№ регистрации	Возраст	Активы-нетто	Уставный фонд	Текущая прибыль	Капитал
	Мосфильмбанк			1,68	1,43	0,01	1,46
	Курганпромбанк			2,33	1,15	0,02	1,49
	Корвет			2,81	1,4	0,01	1,51
	Межрегиональн. Почтовый			3,32	1,2		1,21
	Капиталъ-экспресс			4,26	1,26	0,01	1,64
	Оптбанк			4,61	1,22	0,07	1,36
	Нефтеэнерго-банк			5,03	1,59	0,01	1,57
	Донской народный			5,55	1,52	0,03	1,57
	АКБ Мосуралбанк			7,31	2,97	0,01	3,59
	Алмаззолото			7,38	1,26	0,02	1,72
	Леспромбанк			8,38	2,1	0,01	2,43
	ВТ-Банк			9,34	4,74	0,06	4,83
	Дзержинский			9,82	1,26	0,02	1,5
	Красбанк			10,77	4,89	0,04	4,95
	Кредит-Москва			19,27	2,44	0,03	4,83
	ОАО КБ Центр-Инвест			19,9	3,12	0,09	3,4
	Метрополь			21,84	1,39	0,07	2,63
	Огни Москвы			22,59	1,75	0,33	3,31
	Моск. Банкирский Дом			23,69	5,93	0,14	6,12
	НДБ-Банк			33,37	2,13	0,57	3,38
	Москомприват-банк			39,82	2,02	0,21	4,86
	Абсолют банк			49,55	7,86	0,11	9,53
	Инкасбанк			66,86	7,61	0,08	9,49
	Московский кредитный			68,04	7,53	0,69	19,05
	Газбанк			83,8	5,79	0,51	10,14
	Нижегородпром -стройбанк			89,52	7,61		25,63
	Балтонэксим			102,61	3,73	0,39	7,28
	Московск. Индустриальн.			191,08	3,84	2,12	30,98
	ИНГ Банк			313,36	1,22	9,82	43,17
	Возрождение			322,42	3,88	3,16	17,23

в) По данным задачи вычислить показатели тесноты связи между изучаемыми признаками. В случае линейной связи для оценки тесноты связи необходимо применить формулу линейного коэффициента корреляции, при нелинейной связи – теоретического корреляционного отношения.

Сделать выводы о тесноте и направлении связи между изучаемыми признаками.

Решение:

Таблица 2

Расчетная таблица для определения параметров уравнения регрессии
зависимости чистых активов и капитала коммерческих банков

 

№ банка	Капитал, млн. руб. (Х)	Чистые активы, млн. руб. (Y)	X2	Y2	X*Y	Yх
	9,53	49,55	90,8209	2455,2025	472,2115	64,2658
	9,49	66,86	90,0601	4470,2596	634,5014	63,9861
	25,63	89,52	656,8969	8013,8304	2294,3976	176,8370
	19,05	68,04	362,9025	4629,4416	1296,1620	130,8296
	6,12	23,69	37,4544	561,2161	144,9828	40,4230
	10,14	83,80	102,8196	7022,4400	849,7320	68,5309
	4,95	10,77	24,5025	115,9929	53,3115	32,2424
	4,83	9,34	23,3289	87,2356	45,1122	31,4034
	17,23	322,42	296,8729	103954,6564	5555,2966	118,1042
	30,98	191,08	959,7604	36511,5664	5919,6584	214,2442
	7,28	102,61	52,9984	10528,8121	747,0008	48,5338
	3,40	19,90	11,5600	396,0100	67,6600	21,4048
	3,59	7,31	12,8881	53,4361	26,2429	22,7333
	4,83	19,27	23,3289	371,3329	93,0741	31,4034
	3,38	33,37	11,4244	1113,5569	112,7906	21,2650
	2,43	8,38	5,9049	70,2244	20,3634	14,6226
	4,86	39,82	23,6196	1585,6324	193,5252	31,6131
	3,31	22,59	10,9561	510,3081	74,7729	20,7755
	1,57	5,03	2,4649	25,3009	7,8971	8,6094
	1,57	5,55	2,4649	30,8025	8,7135	8,6094
	1,46	1,68	2,1316	2,8224	2,4528	7,8403
	1,51	2,81	2,2801	7,8961	4,2431	8,1899
	2,63	21,84	6,9169	476,9856	57,4392	16,0210
	1,72	7,38	2,9584	54,4644	12,6936	9,6582
	1,50	9,82	2,2500	96,4324	14,7300	8,1200
	1,64	4,26	2,6896	18,1476	6,9864	9,0989
	43,17	313,36	1863,6489	98194,4896	13527,7512	299,4766
	1,36	4,61	1,8496	21,2521	6,2696	7,1411
	1,21	3,32	1,4641	11,0224	4,0172	6,0923
	1,49	2,33	2,2201	5,4289	3,4717	8,0501
ИТОГО	231,86	1550,31	4691,4386	281396,1993	32257,4613	1550,1251

Рис. 1. График зависимости между величиной капитала и чистыми активами

 

Анализ рисунка 1 показывает наличие связи близкой к прямолинейной.

Система нормальных уравнений для нахождения параметров линейной регрессии методом наименьших квадратов имеет вид:

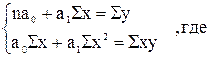
a₀ –усредненное влияние на результативный признак не учтенных в уравнении факторных признаков.

а₁ – коэффициент регрессии, который показывает насколько в среднем изменяется значение результативного признака при изменении факторного на единицу собственного измерения

n – объем совокупности

 

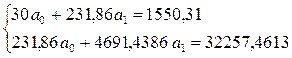
С увеличением капитала банка на 1 млн. рублей чистые активы возрастают на 6,992 млн. рублей.

 

в) Линейный коэффициент корреляции рассчитывается по формуле:

Вывод: по тесноте связь между признаками близкая к существенной, по направлению связь прямая (связь, при которой с увеличением или уменьшением значений факторного признака соотносительно увеличивается или уменьшается значение результативного признака (положительная по значению)).

 

Задача № 4

По данным «Российского статистического ежегодника» (раздел 13. Добыча полезных ископаемых, обрабатывающие производства, производство и распределение электроэнергии, газа и воды) выполнить следующее:

1. Выбрать интервальный ряд динамики, состоящий из 8-10 уровней.

2. Изобразить графически динамику ряда с помощью статистической кривой.

3. По данным выбранного ряда вычислить абсолютные и относительные показатели динамики. Результаты расчетов изложить в табличной форме.

4. Вычислить средние показатели динамики.

5. По данным задачи произвести сглаживание изучаемого ряда динамики с помощью скользящей средней и аналитического выравнивания. Расчетные уровни нанести на построенный ранее график.

Таблица 3