Схема полного исследования функции

1. Найти область определения функции.

2. Определить точки пересечения ее графика с осями координат, точки разрыва функции.

3. Исследовать функцию на монотонность и экстремум.

4. Определить интервалы выпуклости и вогнутости, точки перегиба.

5. Найти асимптоты графика функции.

ПРИМЕР 3. Провести полное исследование функции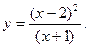

1. Областью определения функции является множество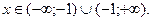

2. Точки пересечения графика данной функции с осями координат: (2;0) , (0;4). Точкой разрыва является x=-1.

3. Исследуем функцию на монотонность и экстремум. Для этого найдем производную и приравняем её к нулю.

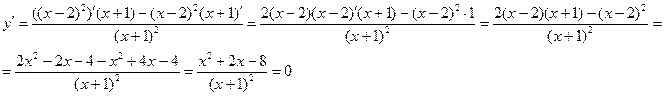Приравняем производную к нулю

Решая квадратное уравнение , получим

В интервале 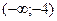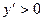(производная больше нуля), следовательно, функция возрастает.

В интервале 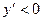функция убывает.

В интервале (-1;2) 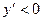функция убывает.

В интервале 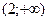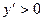функция возрастает.

Определим экстремум. Так как при переходе через точку x=-4 производная меняет свой знак с + на – в этой точке функция имеет локальный максимум : значение функции в этой точке y(-4)=-12. При переходе через точку x=-1 производная не меняет своего знака, следовательно, в этой точке нет экстремума. При переходе через точку x=2 производная меняет свой знак с – на +, следовательно, в точке x=2 функция имеет локальный минимум: значение функции в этой точке y(2)=0.

4. Исследуем график функции на выпуклость и вогнутость. Определим точки перегиба. Для этого найдем вторую производную и приравняем ее к нулю.

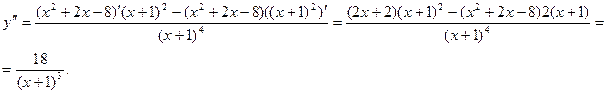
Приравняем вторую производную к нулю 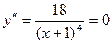. Очевидно, что в интервале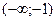 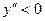, значит кривая выпукла. В интервале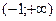 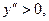кривая вогнута. Так как при x=-1 функция не определена, то точка перегиба отсутствует.

5. Найдем асимптоты графика функции. Т.к. x=-1 является точкой разрыва, то она является вертикальной асимптотой, причем:

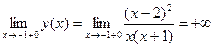
Находим асимптоты:

,

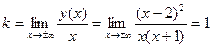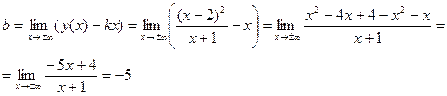
Таким образом, существует единственная наклонная асимптота f(x)=x-5.

ПРИМЕР 4. Провести полное исследование функции

1. Область определения функции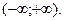

2. Так как y=0 при x=0, то график функции проходит через начало координат.

3. Исследуем функцию на монотонность.

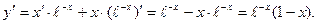
Если 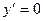, то 1-x=0, откуда x=1. Эта точка разбивает числовую ось на два интервала:

В интервале 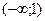, 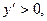и функция в этом интервале возрастает;

В интервале 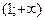, 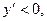и функция убывает. Таким образом, в точке x=1 будем иметь локальный максимум (т.к. знак производной меняется с плюса на минус): значение функции в этой точке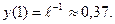

4. Исследуем свойства функции, связанные со второй производной: 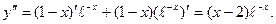Приравняем вторую производную к нулю, получим x=2.

В интерв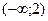але т.е. кривая выпукла в этом интервале.

В интервале 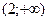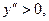т.е. кривая вогнута. Так как в точке x=2 вторая производная 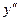меняет знак с минуса на плюс, то в этой точке график функции имеет перегиб:

5. Найдем асимптоты. Вертикальных асимптот нет. Ищем наклонные асимптоты в виде y=kx+b.

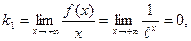
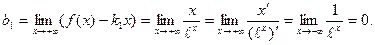Таким образом, прямая y=0 – горизонтальная асимптота при Значит, при наклонных асимптот нет.