СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ. По исходным данным (табл

ЗАДАНИЕ 2

 

По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:

1. Установить наличие и характер корреляционной связи между признаками кредиты и прибыль, образовав пять групп с равными интервалами по каждому из признаков, используя метод аналитической группировки.

2. Измерить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.

3. Оценить статистическую значимость показателя силы связи.

Сделать выводы по результатам выполнения задания 2.

 

Выполнение задания 2

Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.

По условию Задания 2 факторным является признак Кредиты, результативным – признак Прибыль.

 

1. Установление наличия и характера корреляционной связи между признаками Кредиты и Прибыль методом аналитической группировки

Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.

Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х- Кредиты и результативным признаком Y - Прибыль. Макет аналитической таблицы имеет следующий вид (табл. 7):

Таблица 7 - Зависимость прибыли от кредитов

Номер группы	Группы банков по кредитам , млрд.руб. x	Число банков fj	Прибыль, млрд. руб.
всего	в среднем на один банк
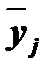
				5=4:3
	ИТОГО

Групповые средние значения получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8:

 

Таблица 8 - Зависимость прибыли от кредитов

Номер группы	Группы банков по кредитам, млрд.руб. x	Число банков, fj	Прибыль, млрд. руб.
всего	в среднем на один банк
				5=4:3
	3,4-5,4		0,36	0,09
	5,4-7,4		0,91	0,15
	7,4-9,4		2,36	0,21
	9,4-11,4		1,44	0,24
	11,4-13,4		0,93	0,31
	ИТОГО		6,00	0,20

Вывод. Анализ данных табл. 8 показывает, что с увеличением кредитов от группы к группе систематически возрастает и средний объем прибыли по каждой группе банков, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.

2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения

Коэффициент детерминации характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии признака Y в его общей дисперсии :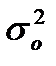

где – общая дисперсия признака Y,

– межгрупповая (факторная) дисперсия признака Y.

Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле

,

где y_i – индивидуальные значения результативного признака;

– общая средняя значений результативного признака;

n – число единиц совокупности.

Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле

,

где – групповые средние,

– общая средняя,

–число единиц в j-ой группе,

k – число групп.

Для расчета показателей и необходимо знать величину общей средней , которая вычисляется как средняя арифметическая простая по всем единицам совокупности:

Значения числителя и знаменателя формулы имеются в табл. 8 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю :

= =0,200 млрд. руб.

Для расчета общей дисперсии применяется вспомогательная таблица 9.

Таблица 9 - Вспомогательная таблица для расчета общей дисперсии

Номер банка	Прибыль, млрд.руб.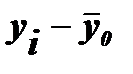
	0,08	-0,1200	0,0144
	0,06	-0,1400	0,0196
	0,13	-0,0700	0,0049
	0,09	-0,1100	0,0121
	0,10	-0,1000	0,0100
	0,16	-0,0400	0,0016
	0,12	-0,0800	0,0064
	0,19	-0,0100	0,0001
	0,18	-0,0200	0,0004
	0,16	-0,0400	0,0016
	0,22	0,0200	0,0004
	0,29	0,0900	0,0081
	0,15	-0,0500	0,0025
	0,16	-0,0400	0,0016
	0,23	0,0300	0,0009
	0,19	-0,0100	0,0001
	0,19	-0,0100	0,0001
	0,18	-0,0200	0,0004
	0,22	0,0200	0,0004
	0,26	0,0600	0,0036
	0,27	0,0700	0,0049
	0,20	0,0000	0,0000
	0,24	0,0400	0,0016
	0,22	0,0200	0,0004
	0,29	0,0900	0,0081
	0,28	0,0800	0,0064
	0,21	0,0100	0,0001
	0,24	0,0400	0,0016
	0,35	0,1500	0,0225
	0,34	0,1400	0,0196
Итого	6,00	-	0,1544

Рассчитаем общую дисперсию: =

Общая дисперсия в данном случае измеряет вариацию результативного признака Прибыль, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных).

Для расчета межгрупповой дисперсии строится вспомогательная таблица 10. При этом используются групповые средние значения из табл. 8 (графа 5).

Таблица 10 - Вспомогательная таблица для расчета межгрупповой дисперсии

Группы банков по кредитам, млрд.руб., x	Число банков, fj	Среднее значение прибыли в группе, млрд. руб.
3,4-5,4		0,09	-0,1100	0,0484
5,4-7,4		0,15	-0,0483	0,0140
7,4-9,4		0,21	0,0145	0,0023
9,4-11,4		0,24	0,0400	0,0096
11,4-13,4		0,31	0,1100	0,0363
ИТОГО		0,20	-	0,1106

 

Рассчитаем межгрупповую дисперсию:

Межгрупповая дисперсия 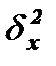в данном случае измеряет систематическую вариацию результативного признака Прибыль, обусловленную влиянием признака-фактора Х Кредит, по которому произведена группировка.

Определяем коэффициент детерминации:

или 72,1%

Вывод. 72,1% вариации прибыли обусловлено вариацией объема кредитов, а 27,9% – влиянием прочих неучтенных факторов.

Эмпирическое корреляционное отношение оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

Значение показателя изменяются в пределах 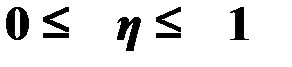. Чем ближе значение к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе служит шкала Чэддока (табл. 11):

Таблица 11 - Шкала Чэддока

h	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика силы связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

 

Рассчитаем показатель :

Вывод: согласно шкале Чэддока связь между объемом кредитов и прибылью является тесной.

3. Оценка статистической значимости коэффициента детерминации . Показатели 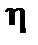и рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи 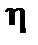, несут в себе элемент случайности. Ввиду этого, необходимо проверить, насколько заключение о тесноте и силе связи, сделанное по выборке, будет правомерными и для генеральной совокупности, из которой была произведена выборка.

Проверка выборочных показателей на их неслучайность осуществляется в статистике с помощью тестов на статистическую значимость (существенность) показателя. Для проверки значимости коэффициента детерминации служит дисперсионный F-критерий Фишера, который рассчитывается по формуле

,

где n – число единиц выборочной совокупности,

m – количество групп,

– межгрупповая дисперсия,

– дисперсия j-ой группы (j=1,2,…,m),

– средняя арифметическая групповых дисперсий.

Величина рассчитывается, исходя из правила сложения дисперсий:

,

где – общая дисперсия.

Для проверки значимости показателя рассчитанное значение F-критерия F_расч сравнивается с табличным F_табл для принятого уровня значимости и параметров k1, k2, зависящих от величин n и m : k₁=m-1, k₂=n-m. Величина F_табл для значений , k_1, k₂ определяется по таблице распределения Фишера, где приведены критические (предельно допустимые) величины F-критерия для различных комбинаций значений , k_1, k₂. Уровень значимости в социально-экономических исследованиях обычно принимается равным 0,05 (что соответствует доверительной вероятности Р=0,95).

Если F_расч>F_табл, коэффициент детерминации признается статистически значимым, т.е. практически невероятно, что найденная оценка обусловлена только стечением случайных обстоятельств. В силу этого, выводы о тесноте связи изучаемых признаков, сделанные на основе выборки, можно распространить на всю генеральную совокупность.

Если F_расч<F_табл, то показатель считается статистически незначимым и, следовательно, полученные оценки силы связи признаков относятся только к выборке, их нельзя распространить на генеральную совокупность.

Фрагмент таблицы Фишера критических величин F-критерия для значений =0,05; k₁=3,4,5; k₂=24-35 представлен ниже:

Таблица 12 – Таблица Фишера

	k2
k1
	3,01	2,99	2,98	2,96	2,95	2,93	2,92	2,91	2,90	2,89	2,88	2,87
	2,78	2,76	2,74	2,73	2,71	2,70	2,69	2,68	2,67	2,66	2,65	2,64
	2,62	2,60	2,59	2,57	2,56	2,55	2,53	2,52	2,51	2,50	2,49	2,48

 

Расчет дисперсионного F-критерия Фишера для оценки =72,1%, полученной при 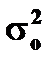=0,0043, =0,0031:

F_расч

Табличное значение F-критерия при = 0,05:

Таблица 13 – Показатели для оценки F-критерия

n	m	k1=m-1	k2=n-m	Fтабл ( ,4, 26)
				2,6

 

Вывод: поскольку F_расч>F_табл, то величина коэффициента детерминации =72,1% признается значимой (неслучайной) с уровнем надежности 95% и, следовательно, найденные характеристики связи между признаками Кредит и Прибыль правомерны не только для выборки, но и для всей генеральной совокупности предприятий.

 

 

ЗАДАНИЕ 3

 

По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:

1) ошибку выборки для средней величины кредита банка и границы, в которых будет находиться средняя величина кредита для коммерческих банков генеральной совокупности.

2) ошибку выборки доли банков с размером кредита 9,4 млрд.руб. и более и границы, в которых будет находиться генеральная доля.

 

Выполнение Задания 3

Целью выполнения данного Задания является определение для генеральной совокупности банков границ, в которых будут находиться средняя величина кредита, и доля банков с величиной кредитов 9,4 млрд.руб. и более.

 

1. Определение ошибки выборки для величины кредитов, а также границ, в которых будет находиться генеральная средняя

Применяя выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки репрезентативности), т.к. генеральные и выборочные характеристики, как правило, не совпадают, а отклоняются на некоторую величину ε. Принято вычислять два вида ошибок выборки - среднюю и предельную . Для расчета средней ошибки выборки применяются различные формулы в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную. Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка для выборочной средней определяется по формуле

,

где – общая дисперсия изучаемого признака,

N – число единиц в генеральной совокупности,

n – число единиц в выборочной совокупности.

Предельная ошибка выборки определяет границы, в пределах которых будет находиться генеральная средняя:

,

,

где – выборочная средняя,

– генеральная средняя.

Предельная ошибка выборки кратна средней ошибке с коэффициентом кратности t (называемым также коэффициентом доверия):

Коэффициент кратности t зависит от значения доверительной вероятности Р, гарантирующей вхождение генеральной средней в интервал , называемый доверительным интервалом.

Наиболее часто используемые доверительные вероятности Р и соответствующие им значения t задаются следующим образом (табл. 14):

Таблица 14 – Доверительные вероятности

Доверительная вероятность P	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

По условию Задания 2 выборочная совокупность насчитывает 30 банков, выборка 3% механическая, следовательно, генеральная совокупность включает 1000 банков. Выборочная средняя , дисперсия определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 15:

Таблица 15 – Значения для вычислений

Р	t	n	N
0,954				8,3	5,3

Рассчитаем среднюю ошибку выборки:

млрд.руб.

Рассчитаем предельную ошибку выборки:

Определим доверительный интервал для генеральной средней:

Вывод. На основании проведенного выборочного обследования с вероятностью 0,954 можно утверждать, что для генеральной совокупности банков средняя величина кредита находится в пределах от 7,5 до 9,1 млрд.руб.

 

2. Определение ошибки выборки для доли банков со величиной кредита 9,4 млрд.руб. и более, а также границ, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

,

где m – число единиц совокупности, обладающих заданным свойством;

n – общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки доли единиц, обладающих заданным свойством, рассчитывается по формуле

,

где w – доля единиц совокупности, обладающих заданным свойством;

(1-w) – доля единиц совокупности, не обладающих заданным свойством,

N – число единиц в генеральной совокупности,

n– число единиц в выборочной совокупности.

Предельная ошибка выборки определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:

m=9

Рассчитаем выборочную долю:

Рассчитаем предельную ошибку выборки для доли:

Определим доверительный интервал генеральной доли:

0,135 0,465

или

13,5% 46,5%

Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности банков доля банков с величиной кредитов 9400 млрд.руб.и более будет находиться в пределах от 13,5% до 46,5%.

 

ЗАДАНИЕ 4

 

Имеются следующие данные о кредитовании банком промышленных предприятий, млрд.руб.

Таблица 16 – Данные о кредитовании

Предприятие	Средние остатки кредитов	Погашение кредитов
Базисный период	Отчетный период	Базисный период	Отчетный период

 

Определить:

1. По каждому предприятию и двум предприятиям вместе за каждый год:

– однодневный оборот по погашению;

– длительность пользования кредитом.

2. Динамику изменения длительности пользования кредитом по каждому предприятию. Рассчитанные показатели представить в таблице.

3. Индексы средней длительности пользования кредитом переменного, постоянного состава, структурных сдвигов.

4. Сделать выводы.

Выполнение задания 4

Для вычисления однодневного оборота по погашению используем по формуле:

Где О_П – оборот кредита по погашению

D - число дней в периоде

Для вычисления длительности пользования кредитом используем формулу:

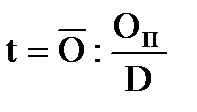
Где - средний остаток кредита

Все необходимые расчеты выполнены в таблице.

Таблица 17 – Расчетная таблица

№ строки	Показатель	Предприятие
	Средние остатки кредитов в базисном периоде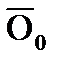
	Средние остатки кредитов в отчетном периоде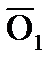
	Погашение кредитов в базисном периоде ОП0
	Погашение кредитов в отчетном периоде ОП1
	Однодневный оборот по погашению m0=стр.3/360	2,083	1,986
	Однодневный оборот по погашению m1=стр.4/360	3,305	2,000
	Длительность пользовании кредитом в базисном периоде t0=стр.1/стр.5	72,01	65,46
	Длительность пользования кредитом в отчетном периоде t1=стр.2/стр.6	51,44	67,5

 

Вычислим индексы средней длительности пользования кредитом переменного, постоянного состава, структурных сдвигов.

Индекс переменного состава:

Индекс средней длительности пользования кредитом переменного состава показывает ее абсолютное и относительное изменения за счет влияния двух факторов: 1) изменения длительности пользования кредитом на предприятиях; 2) структурных сдвигов в однодневном обороте.

Абсолютное изменение средней длительности пользования кредитом за счет двух факторов: дня

Индекс постоянного состава:

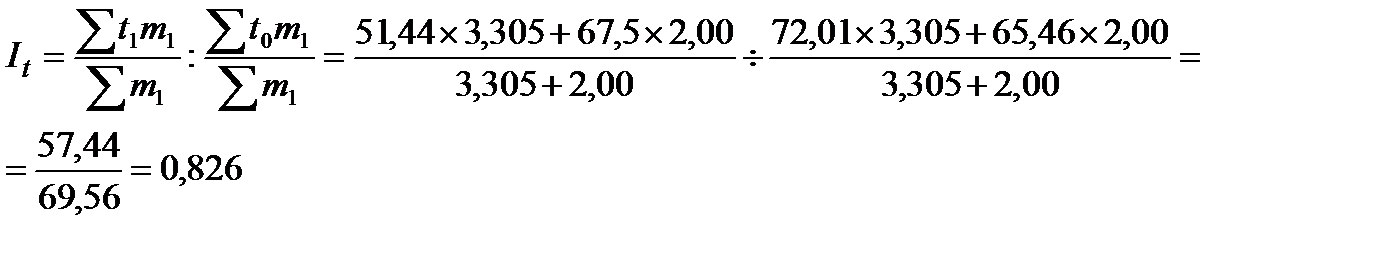
Индекс средней длительности пользования кредитом постоянного состава – характеризует ее относительное и абсолютное изменения при изменениях длительности пользования кредитом на предприятиях.

Абсолютное изменение средней длительности пользования кредитом за счет снижения длительности пользования кредитом на предприятиях:

дня

Индекс структурных сдвигов:

Индекс структурных сдвигов – показывает абсолютное и относительное изменения средней длительности пользования кредитом за счет структурных сдвигов в однодневном обороте.

Абсолютное изменение средней длительности пользования кредитом за счет структурных сдвигов в однодневном обороте: 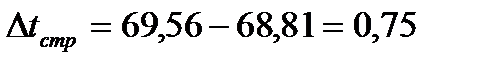дня.

Для изучения влияния отдельных факторов на изменение средней длительности использования кредитом строится система взаимосвязанных индексов:

,

Вывод: анализ индексов показывает, что средняя длительность пользования кредитом в отчетном году сократилась на 16,5% или на 11,37 дня за счет двух факторов: снижения длительности пользования кредитом на предприятиях на 17,4% или на 12,12 дня; повышения длительности пользования кредитом вследствие структурных сдвигов в однодневном обороте на 1,1% или на 0,75 дня. Структурные сдвиги оказали неблагоприятное влияние на среднюю длительность пользования кредитом.

 

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 

1. Богородская Н.А. Статистика финансов: Учебное пособие. – Изд. 2-е перераб. и доп. – М.: ООО Фирма «Благовест-В», 2005 г. – 248 с.

2. Елисеева И. И., Юзбашев М.М. Общая теория статистика: Учебник / Под ред.И.И.Елисеевой. –М.: Финансы и статистика, 2008-368с.: ил.

3. Енюков И.С. методы, алгоритмы, программы многомерного статистического анализа. – М.: Финансы и статистика, 2008

4. Ефимова М.П., Петрова Е.В., Румянцева В.Н. Общая теория статистики: Учебник. – М.: Инфра-М, 2008-415с.

5. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учбник/А.И. Харламов, О.Э. Башина, В.Т. Бабарин и др. Под ред. А.А. Спирина, О.Э. Башина.-М.: Финансы и статистика, 2007-296 с.:ил.

6. Статистика: учебное пособие для высших учебных заведений по экономическим специальностям / В.М. Гусаров, Е.И.Кузнецова. – М: ЮНИТИ-ДАНА, 2007. – 479 с.

7. Статистика: теория и практика в Excel: учебное пособие / В.С.Лялин, И.Г. Зверева, Н.Г. Никифорова. – М.: Инфра-М, 2010. – 446.

8. Статистика финансов: учебник / [М.Г.Назаров и др.]. - М.: Омела-Л, 2008. -460 с.