ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

 

Факультет ЭФ Направление 080100 «Экономика», профиль «Коммерция»_________

Кафедра ЭФ-3 «Коммерция и маркетинговые исследования»____________________

Дисциплина «Организация коммерческой деятельности предприятия»__________

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе на тему:

«________________________»

 

Студент ____________________________ _____________________

фамилия и инициалы подпись

Группа __ЭФ-3-_________________________шифр_____________________________

Обозначение работы____КР-2068752-080301/53365-ЭФ-3-19-13_________________

Работа защищена на оценку________________

Руководитель работы _______________ __Егоров Ю.Н._____

фамилия и инициалы подпись

 

Члены комиссии:

_________________ _____________________

подпись фамилия и инициалы

_________________ _____________________

подпись фамилия и инициалы

_________________ _____________________

подпись фамилия и инициалы

 

Москва, 2014

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Факультет ЭФ Направление 080100 «Экономика», профиль «Коммерция»_________

Кафедра ЭФ-3 «Коммерция и маркетинговые исследования»____________________

Дисциплина «Организация коммерческой деятельности предприятия»__________

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Студент_группа_____________шифр_________

1. Тема: «_____________________________

____________________»

2. Срок предоставления работы к защите «___» ___________________2013 г.

3. Исходные данные для разработки__________

_______

4. Содержание пояснительной записки:

Задание на курсовую работу

Содержание

Введение

1 глава ______________________________

1.1

1.2

1.3

1.4

1.5

2. глава______________________________

2.1

2.1.1

2.1.2

2.1.3

2.2

2.2.1

2.2.2

2.2.3

Заключение

Список использованных источников

Руководитель работы _______________ __Егоров Ю.Н._____

фамилия и инициалы подпись

 

 

Задание принято к исполнению _______________ _________________

фамилия и инициалы подпись

 

Содержание

 

Введение 4

1. Оптимизационные модели. Общая информация 6

1.1 Предпосылки к созданию оптимизационных моделей 6

1.2 Понятие оптимизационных задач и оптимизационных моделей 9

1.3 Экономические основы оптимизации 11

1.4 Общая запись оптимизационной экономической задачи 12

1.5 Классификация оптимизационных моделей и методов их реализации 13

2. Виды оптимизационных моделей, используемых в коммерческой логистике 16

2.1 Транспортная задача 16

2.1.1 Историческая справка 16

2.1.2 Основное содержание и цели транспортной задачи 17

2.1.3 Общий вид транспортной задачи 18

2.2 EOQ-модель 22

2.2.1 Общая характеристика модели 22

2.2.2 Расчет оптимальной партии поставки 23

2.2.3 Варианты работы с EOQ-моделью 25

Заключение 33

Список источников 34

 

Введение

 

Успешность решения подавляющего большинства экономических задач зависит от наиболее эффективного способа использования ресурсов (денег, товаров, сырья, оборудования, рабочей силы и др.). Именно эффективностью использования, как правило, ограниченных, ресурсов определяется конечный результат деятельности любой экономической системы (фирмы, предприятия, отрасли).

Экономическая суть методов оптимизации заключается в том, что, исходя из наличия определенных ресурсов, выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя.

Актуальность темы обусловлена тем, что поиск оптимальных решений с помощью оптимизационных моделей необходим для коммерческой логистики. А коммерческая логистика есть организация управления экономическими системами в сфере товарного обращения. Следовательно, модели оптимизации отлично дополняют область логистики, и, по мнению автора, каждый, кто выбрал профессию логиста, обязан знать базовые оптимизационные модели.

Главные объекты исследования – оптимизационные модели. Предметы исследования – виды оптимизационных моделей, применяемых в коммерческой логистике.

Цель данной курсовой работы – рассмотреть в 1-ой главе в общем виде оптимизацию и оптимизационные модели, а после – подробно описать во 2-ой главе те модели, которые используются непосредственно в коммерческой логистике.

Задачи курсовой работы:

- дать определение оптимизационным моделям;

- описать предпосылки созданию моделей;

- выяснить, какое их экономическое назначение;

- описать классификацию моделей;

- подробно рассказать о моделях, применяемых в коммерческой логистике.

В основе курсовой работы лежат работы Д. Данцига, В. Сергеева, Л. Канторовича, И.В. Орлова, В.В. Федосеева, а также использовались различные интернет-ресурсы.

Метод исследования, используемый при выполнении данной курсовой работы – теоретический анализ, подразумевающий сбор данных с последующим выявлением общих признаков, на основе которых составляются общие выводы.

 

1. Оптимизационные модели. Общая информация.

1.1 Предпосылки к созданию оптимизационных моделей

Оптимизация - поиск наилучшего решения с учетом ограничений.

Для оптимизации ищется целевая функция. Эта функция конструируется искусственно на основе уравнений, описывающих объект оптимизации. Целевая функция обычно имеет много аргументов: φ=f (х1, х2, ..., х n).

Чтобы найти оптимальное значение, перебирают значение аргументов хi пошагово до тех пор, пока значение φ станет удовлетворять условиям оптимума. Даже количество аргументов не более трех, "тупой" перебор может потребить очень много времени.

Поэтому разработаны десятки методов оптимизации:

- первый строгий математический метод предложил в 1840г. венгерский математик Огюст Коши - МСС - метод скорейшего спуска. При формулировании задач оптимизации обычно стараются ее свести к поиску минимума. МСС относится к классу градиентных методов.

Градиент - вектор, указывающий на направление максимального возрастания функции.

Антиградиент - вектор, указывающий на направление максимального убывания функции. Чтобы повернуть вектор на 180╟, достаточно изменить все знаки у градиентов на противоположные (т.е. х (-1)).

Для иллюстрации поиска экстремума в процессе оптимизации функций двух переменных используют линии равного уровня (ЛРУ). Если задаться постоянным значением φ и так подбирать значения хi чтобы значение φ было равным заданному значению, то геометрическое место точек φ составит линию равного уровня.

^ В зависимости от целевой функции линий равного уровня могут характеризоваться следующими географическими понятиями:

Долина - когда соседние линии равного уровня изменяется очень слабо в широком диапазоне аргументов.

Возвышенность - когда соседние линии равного уровня представляют собой замкнутые линии и значение φ возрастает от внешних линий к внутренним.

Впадина - когда соседние линии равного уровня представляют собой замкнутые линии, и значение φ убывает от внешних линий к внутренним.

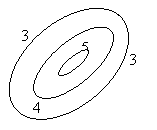
Седловина - локальный минимум, в центре которого векторы указывают на возрастание функции, но вскоре направление вектора резко изменяется вверх или вниз.

МСС - простейший метод оптимизации, пригодный для сложных систем. Работа метода хорошо иллюстрируется с помощью линий равного уровня (ЛРУ).

Порядок поиска оптимума:

- выбирается исходная точка в виде значений параметров целевой функции:
φ=f (х1, х2, ..., х n).
- ищется градиент;
- движемся в направлении антиградиента с заданным шагом;
- на каждом шаге проверяем выполнение условия движения, оно такое: φi < φi-1 ( текущее значение φ должно быть меньше предыдущего).
- если условие движения нарушается, то процесс останавливается, иначе, движение продолжается;
- при нарушении условий движения уточняется одномерный минимум и ищется новый градиент;
- условие останова:

а) значение φ меньше заданного;
б) разность значений соседних φ меньше заданной;
в) количество шагов превышает допустимое.

- если после останова минимума не удовлетворяет требованиям, то либо ищется другая исходная точка и процесс повторяется, либо выбирается другой метод оптимизации.

 

1.2Понятие оптимизационных задач и оптимизационных моделей

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

 

Оптимальная или оптимизационная модель [optimization model] — экономико-математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них.

Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов:

 

- управляемых переменных;

- неуправляемых переменных;

- формы функции (вида зависимости между ними).

Область допустимых решений это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются:

а) на линейные ( ^ I и II ) и нелинейные ( III и IV ) (рис. 3.1);

б) детерминированные ( А , В ) и стохастические (группы кривых С _i ) (рис. 3.2).

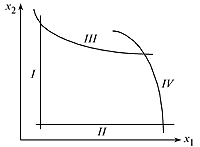Рисунок 3.1– Линейные и нелинейные ограничения

Рисунок 3.2– Детерминированные и стохастические ограничения

Стохастические ограничения являются возможными, вероятностными, случайными.

ОЗ решаются методами математического программирования, которые подразделяются на:

 

- линейное программирование;

- нелинейное программирование;

- динамическое программирование;

- целочисленное программирование;

- выпуклое программирование;

- исследование операций;

- геометрическое программирование и др.

Главная задача математического программирования это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.

1.3 Экономические основы оптимизации.

Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении.

Необходимым условием использования принципа оптимальности (оптимального подхода к планированию и управлению) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать те или иные управленческие решения. Именно такими, как правило, и являются ситуации, составляющие повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и загрузка контейнеров и т.д.).

Суть принципа оптимальности состоит в стремлении выбрать такое управленческое решение Х = (х₁, х₂, …, х_n), где х_j, j = 1, ..., n, - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.

«Наилучшим образом» здесь означает выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных управленческих решений. Традиционные критерии оптимальности в экстремальных моделях — «максимум прибыли», «минимум затрат», «максимум объема работ (услуг)» и др.

«Учитывало бы внутренние возможности и внешние условия производственной деятельности» означает, что на выбор управленческого решения (поведения) накладывается ряд условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D.

Таким образом, реализовать на практике принцип оптимальности в планировании и управлении — это значит решить экстремальную задачу вида:

max (min) f(X) (1.1)

X ∈ D (1.2)

где f(X) - математическая запись критерия оптимальности - целевая функция.

1.4 Общая запись оптимизационной экономической задачи

Задачу условной оптимизации (1.1), (1.2) обычно записывают в виде:

найти максимум или минимум функции

f(X) = f(х₁, х₂, … х_n) (1.3)

при ограничениях

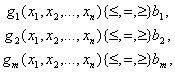(1.4)

x_j ≥ 0, j = 1, 2, ..., n. (1.5)

Условие (1.5) необязательно, но его всегда можно добиться. Обозначение {≤, =, ≥} говорит о том, что в конкретном ограничении возможен один из знаков <, = или >. Более компактная запись выглядит следующим образом:

max (min) f(х₁, х₂, … х_n) (1.6)

g_i(x₁, x₂, …, х_n) {≤, =, ≥} b_i, i = 1, 2, ..., m (1.7)

x_j ≥ 0, j = 1, 2, ..., n. (1.8)

Задача (1.6)—(1.8) — общая задача оптимального (математического) программирования, другими словами, математическая модель задачи оптимального программирования в основе построения (разработки) которой лежат принципы оптимальности, системности и адекватности.

1.5 Классификация оптимизационных моделей и методов их реализации.

Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.

1. По характеру взаимосвязи между переменными —

а) линейные,

б) нелинейные.

В случае а) все функциональные связи в системе ограничений и функция цели — линейные функции; наличие нелинейности в хотя бы одном из упомянутых элементов приводит к случаю б).

2. По характеру изменения переменных —

а) непрерывные,

б) дискретные.

В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область, в случае б) все или хотя бы одна переменная могут принимать некоторые целочисленные значения.

3. По учету фактора времени —

а) статические,

б) динамические.

В задачах а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается управленческое решение; в случае б) такое предположение достаточно аргументировано принято не может быть.

4. По наличию информации о переменных —

а) задачи в условиях полной определенности (детерминированные),

б) задачи в условиях неполной информации (случай риска),

в) задачи в условиях неопределенности.

В задачах б) отдельные элементы являются вероятностными величинами, однако дополнительными статистическими исследованиями могут быть установлены их законы распределения вероятностей; в случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.

5. По числу критериев оценки альтернатив —

а) простые (однокритериальные),

б) сложные (многокритериальные) задачи.

Задачи а) — задачи, где экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному; б) многокритериальная оптимизация — выбор управленческого решения по нескольким показателям.

На практике многокритериальный поиск тем или иным способом сводят к однокритериальному: методом последовательных уступок, способом выделения «главного» показателя, оптимизацией по обобщенной целевой функции и др.

В заключение 1-ой главы автор данной курсовой работы отмечает важность оптимизационных моделей и задач линейного программирования: умение пользоваться ими помогает предприятию грамотно воспользоваться ресурсами при их ограниченном количестве. Они позволят логисту учесть ресурсы, которые использует организация в производстве продукции и составить прогноз о том, как оптимально использовать ресурсы, к чему стремится и сам логист.

 

2. Виды оптимизационных моделей, используемых в коммерческой логистике

2.1 Транспортная задача

2.1.1 Историческая справка

Транспортная задача — задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных затратах на перевозку (тарифах) между пунктами отправления и назначения. Является задачей линейного программирования специального вида.

 

Проблема была формализована французским математиком Гаспаром Монжем в 1781 г. Первым, кто изучал транспортную задачу математически, был А. Н. Толстой из СССР. В 1930 г. вышла его работа о поиске минимального общего километража в железнодорожных перевозках, где использовались перераспределительные циклы.

Как проблему линейного программирования (детализация симплекс-метода) ее впервые рассмотрел Дж. Данциг. Другой процесс вычисления («метод одновременного решения прямой и двойственной задач») был предложен Фордом и Фулкерсоном в 1956 г. Способ решения транспортной задачи (методом потенциалов) в СССР был опубликован Канторовичем и Гавуриным в 1949 г. и ранее. В своей книге «Линейное программирование, его применения и обобщения» (М.: Соцэкгиз, 1966) Дж. Данциг ссылается на публикации Канторовича 1939 г. и 1942 г., а также последующую статью 1949 г., содержащие, как он считал, в завершенном виде теорию задачи о перевозках, хотя и с неполным вычислительным алгоритмом, написанные на доступном для расчетчиков языке. К сожалению, по его мнению, эти работы оказались малоизвестными в СССР и за его пределами. В противоположность этому, сам Канторович в своих мемуарах 1987 г. утверждал, что университет немедленно опубликовал его статью, и она была разослана в пятьдесят Народных комиссариатов. По сведениям Данцига, для ЭВМ программа симплекс-метода для случая решения транспортной задачи была впервые разработана в 1950 г. для машины СЕАК, а программа для общего симплекс-метода — в 1951 г. под руководством А. Ордена из ВВС США и А. Д. Гофмана из Бюро стандартов.

2.1.2 Основное содержание и цели транспортной задачи

Значительная часть логистической операции на пути движения материального потока от первичного источника сырья до конечного потребителя осуществляется с помощью различных транспортных средств. Затраты на выполнение этих операций составляют до 50 процентов общих затрат на логистику.

Транспорт представляет собой систему, состоящую из двух под­систем: транспорт общего и не общего использования.

Транспорт общего использования обслуживает сферу обращения и населения. Его часто называют магистральным. Понятие транспор­та общего пользования охватывает: железнодорожный транспорт, водный (морской и речной), автомобильный, воздушный, трубопро­водный.

Транспорт не общего пользования включает внутрипроизводст­венный транспорт, а также транспортные средства всех видов, при­надлежащие не транспортным предприятиям.

Транспорт органично вписывается в производственные и торго­вые процессы. Поэтому транспортная составляющая участвует во многих задачах логистики. Вместе с тем существует достаточно са­мостоятельная транспортная область логистики.

К задачам транспортной логистики в первую очередь относят задачи, решение которых усиливает согласованность действий непо­средственных участников транспортного процесса. К таким задачам относятся:

- обеспечение технического соответствия участников транс­портного процесса (техническое соответствие означает согласован­ность как внутри отдельных видов, так и в межвидовом разрезе, ко­торая позволяет работать с контейнерами, пакетами);

- технологическая сопряженность - подразумевает применение единой технологии транспортировки, прямые перегрузки, беспере­грузочное сообщение:

- экономическая сопряженность - это общая методология ис­следования конъюнктуры рыка и построения тарифной системы, оз­начающие согласование экономических интересов участников транспортного процесса:

- использование единых систем планирования (разработка и применение различных планов графиков для различных видов транспорта);

К задачам транспортной логистики также относят:

- создание транспортных коридоров;

- выбор вида транспорта;

- выбор маршрута транспортировки грузов;

- составление расписаний.

 

2.1.3 Общий вид транспортной задачи

 

На двух станциях отправления А₁ и А₂ сосредоточено соответственно а₁ и а₂ единиц некоторого однородного груза. Этот груз следует доставить в три пункта назначения B₁,B₂,B₃. Причем в каждый из них должно быть завезено соответственно b₁, b,₂ b₃ единиц этого груза. Стоимость перевозки единицы груза из пункта A_i в пункт B_j (обозначим C_ij) считаем заданной. Все данные полезно свести в табл. 1.

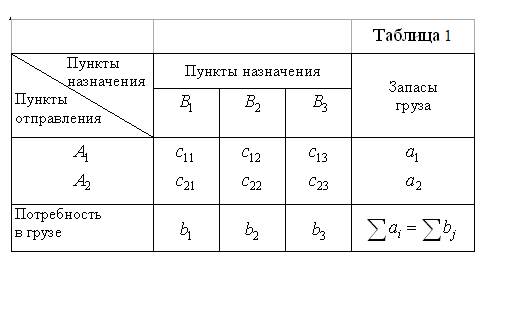
Будем считать, что общий запас грузов на станциях отправления равен суммарной потребности в этом грузе всех станций назначения. Следовательно,

a₁ +a₂ =b₁ +b₂ +b₃. (2.1)

Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.

Обозначим через x_ij количество единиц груза, предназначенного к отправке из пункта A_i в пункт B_j. Тогда количество груза, который планируется к доставке в пункт B₁ из пунктов A₁ и A₂, составит

x₁₁ + x₂₁.

Так как потребность в грузе B₁ равна b₁, то должно выполняться равенство:

x₁₁ + x₂₁ = b₁.

Аналогично получим равенства

x₁₂ + x₂₂ = b₂

x₁₃ +x₂₃ = b3

С другой стороны, общее количество груза, отправленного со станции A₁, выражается суммой

x₁₁ + x₁₂ + x₁₃ ,

которая, очевидно, обязана совпадать с запасом a₁ груза, сосредоточенным на этой станции, то есть

x₁₁ + x₁₂ + x₁₃ = a₁.

Подобно этому

x₂₁ + x₂₂ + x₂₃ = a₂

Полученные соотношения легче запомнить, если все величины свести в так называемую матрицу перевозок (см. табл. 2). Тогда легко проверить, что сумма всех x_ij, расположенных на i-ой строке, равна запасу a₁ в пункте назначения A₁. Сумма же всех x_ij из столбца j равна потребности b_j пункта назначения B_j.

Из условий задачи с очевидностью вытекает, что общая стоимость F всех перевозок равна

.

Таким образом, математическая формулировка транспортной задачи (по критерию стоимости перевозок) такова. Задана система

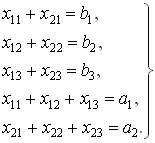(2.2)

пяти линейных алгебраических уравнений с шестью неизвестными и линейная форма

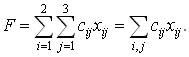(2.3)

Требуется среди всех неотрицательных решений x_ij системы (2.2) выбрать такое, при котором форма F минимизируется (достигает наименьшего значения). Отметим, что при решении транспортной задачи следует учитывать важное соотношение, вытекающее из самого условия задачи:

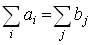. (2.1')

 

2.2 EOQ-модель

 

2.2.1 Общая характеристика модели

Основной целью управления запасами, как одной из составляющих, рабочего капитала является минимизация совокупных расходов на их покупку, доставку и складское хранение. При этом расходы на доставку и хранение демонстрируют разнонаправленное поведение. С одной стороны, увеличение партии поставки приводит к снижению расходов на доставку в расчете на единицу запасов, а, с другой стороны, это приводит к росту складских расходов на единицу запасов. Для решения этой задачи Уилсоном (англ. R. H. Wilson) была разработана методика расчета оптимальной партии поставки (англ. Economic Order Quantity, EOQ), известная также как EOQ-модель или формула Уилсона.

Эта модель предполагает следующие допущения:

· спрос (расход) является непрерывным, а интенсивность спроса λ = const;

· период между двумя смежными заказами (поставками) постоянен (τ_c3 = τ_сп = const);

· спрос удовлетворяется полностью и мгновенно;

· транзитный и страховой запасы отсутствуют;

· емкость склада не ограничена;

· затраты на выполнение заказа (с_o) и цена поставляемой продукции в течение планового периода постоянные;

· затраты на поддержание запаса единицы продукции в течение единицы времени постоянные и равны c_h.

Критерием оптимизации размера заказа на пополнение запасов в данной модели является минимум общих затрат на выполнение заказов и поддержание запаса (МР, ГП) на складе в течение планового периода (например, года). Составляющие суммарных затрат по-разному зависят от размера заказа (величины партии поставки), что отражено на графиках (рис. 1).

2.2.2 Расчет оптимальной партии поставки

В основе EOQ-модели лежит функция совокупных расходов (TC), которая отражает расходы на приобретение, доставку и хранение запасов.

p – цена покупки или себестоимость производства единицы запасов;

D – годовая потребность в запасах;

K – стоимость организации заказа (погрузка, разгрузка, упаковка, транспортные расходы);

Q – объем партии поставки.

H – стоимость хранения 1 единицы запасов в течение года (стоимость капитала, складские расходы, страховка и т.п.).

Для того чтобы рассчитать размер оптимальной партии поставки необходимо продифференцировать функцию совокупных расходов относительно переменной Q и приравнять к 0.

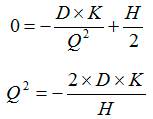
Решив полученное уравнение относительно переменной Q, мы получим оптимальную партию поставки (EOQ).

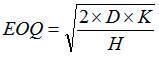
Это и есть формула оптимального размера заказа (Economic order quantity) - формула Вильсона.

Математический вывод формулы Вильсона важен для понимания некоторых её возможностей и ограничений. А понимание нужно, для того чтобы исключить ошибки, возможные при попытках практического применения расширенных возможностей, которые предоставляет эта формула.

Главный вывод, касающийся ограничений использования формулы EOQ, заключён в том, что функция затрат должна быть непрерывной и дифференцируемой на интервале (0; inf). Соответственно задача нахождения оптимального размера поставки будет решаться за один шаг. Изменение алгоритма расчёта, например для анализа системы скидок, приводит к тому, что в функции суммарных затрат появляются точки разрыва первого рода. Формально такая функция не подлежит дифференцированию. Решение задачи заключается в поиске минимальных значений суммарных затрат на каждом из интервалов между точками разрыва и в самих точках. Но этот метод уже будет называться не исследованием функции, а методом перебора значений. Вариантов же, которые нужно посчитать и сравнить между собой, будет ровно столько, сколько будет комбинаций самих параметров в формуле суммарных затрат.

 

2.2.3 Варианты работы с EOQ-моделью

Страховые запасы.

Очень часто отсутствие страховых запасов в модели EOQ считается как одно из ограничений в её использовании. Указывается, что формула Вильсона рассчитана на случай моментального пополнения, без страховых запасов. Что же реально происходит со страховыми запасами? Какое влияние они оказывают на расчёт оптимального размера заказа? Расходы на содержание страховых запасов равны произведению величины страховых запасов на цену единицы ресурсов и на процентную ставку расходов на их содержание:

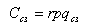
В формулу суммарных затрат введём расходы на содержание страховых запасов. Формула будет следующей:

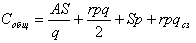
q_сз - количество страховых запасов. Произведение r*p*q_сз является константой. Заметим ещё раз, что q и q_сз - это разные параметры, изменение размера поставки q не влияет на величину страховых запасов q_сз. Поэтому при дифференцировании функции по q это произведение превратится в ноль, и мы получим следующую формулу:

Дальнейшие преобразования полученного уравнения приведут нас опять к формуле EOQ.

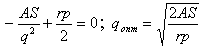
Очевидно, что использование величины страховых запасов в расчётах суммарных затрат ни как не влияет на формулу оптимального размера поставки.

Данный вывод, тем не менее, не означает полную бесполезность величины страховых запасов в формуле суммарных затрат, их использование будет описано ниже, при использовании данной формулы для выбора поставщика.

2) Расходы на содержание запасов.

В книгах можно встретить два вида формулы оптимального размера поставки. Однако формулы приводятся без подробного толкования по их содержанию и особенностям применения:

В первом случае параметр r - обозначается как процентная ставка и умножается на цену единицы товара, измеряется, соответственно, в процентах, во втором случае r - это издержки хранения единицы товара, измеряемые в денежных величинах.

В реальности произведение цены ресурса на процентную ставку более применимо, если рассматриваются только расходы на связанный капитал, а показатель расходов на единицу ресурса, если рассматриваются затраты на хранение, причём затраты на хранение должны быть условно переменными, то есть зависеть от количества хранимых материальных ресурсов.

На самом же деле издержки могут включать как расход на связанный капитал, так и условно - переменные расходы на хранение. Соответственно первые расходы будут равны произведению цены товара на ставку дисконтирования, а вторые - это затраты на хранение единицы товара на складах.

Таким образом, обе формулы имеют недостатки. Первая формула учитывает только финансовые расходы на связанный в запасах капитал и не учитывает складские расходы на хранение. Вторая формула, напротив, учитывает только расходы на хранение ресурсов на складе, но не учитывает расходы, связанные с отвлечением финансовых средств.

Решение данной проблемы заключено в объединении тех и других видов расходов в одной формуле. Поэтому желательно рассматривать расходы на содержание запасов, разделив их на составляющие части, по следующей формуле:

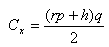
Где r*p - затраты на связанный капитал единицы ресурса, а h - затраты на хранение на складе единицы ресурса. Развёрнутая формула суммарных затрат будет следующей:

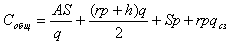
И соответственно формула расчёта оптимального размера поставки, после преобразований, будет иметь вид:

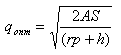
НДС в формуле EOQ.

Ещё одним является вопрос о применении цены и НДС в формуле EOQ. Должна ли цена единицы ресурсов применяться в расчётах оптимального размера поставки с НДС или без НДС? Вопрос обычно появляется при обсуждении и утверждении методологии и инструментов оптимизации управления запасами. Причём этот вопрос обычно возникает в экономических и финансовых службах, а не у закупщиков. Подразделения закупа сталкиваются обычно с одной ценой - той, которую нужно уплатить поставщику. А в финансовом планировании и бюджетировании применяются оба вида цен. Например, цена с НДС используется в бюджете движения денежных средств, а цена без НДС - в экономических расчётах себестоимости продукции и в бюджете доходов и расходов. С одной стороны НДС подлежит уплате поставщику и вроде бы должен участвовать в расчётах, с другой стороны, согласно Налоговому Кодексу РФ, НДС подлежит возмещению и не является расходом, а в описании параметров формулы есть слова "затраты" и "расходы". В книгах упоминания этой проблемы нет.

В данной формуле цена служит для определения расходов на связанный капитал. То есть считаются деньги, потраченные на выполнение заказа (доставку партии), деньги, потраченные на приобретение (вложенные в запасы) и деньги, потраченные на содержание запасов.

Расчёт расходов на связанный капитал, при содержании запасов, должен учитывать денежные суммы, отвлечённые из оборота в связи с приобретением ресурсов. Поэтому, поскольку, поставщику мы выплачиваем денежную сумму по цене товара с НДС, то и в формуле, соответственно мы должны использовать цену товара с НДС. Для удобства, в формуле, при расчёте, цена единицы ресурсов будет использоваться без НДС (p), а НДС будет учтён в виде коэффициента (r_НДС), соответствующего налоговой ставке:

Для случая, если ставка НДС составляет 20% - коэффициент rНДС будет равен 1,2, если ставка НДС составляет 10%, то коэффициент r_НДС будет равен 1,1 и если приобретаемые материальные ресурсы не облагаются НДС, то есть ставка НДС составляет 0%, то коэффициент r_НДС будет равен 1,0.

По законодательству РФ, НДС, уплаченный поставщику, подлежит возмещению. Но возмещение возможно не ранее, чем от покупателя будет получена оплата за готовую продукцию. Можно предположить, что данная формула справедлива только для случаев, когда возмещение НДС осуществляется после использования ресурсов в производстве, причём эти случаи являются типичными в российской практике. Но с другой стороны, если рассматривать оптимизацию управления и сырьевыми запасами и запасами готовой продукции в целом, то уплата НДС должна относиться к задаче оптимизации затрат на входной материальный поток. Возмещение же НДС является задачей оптимизации затрат выходящего потока. Потому можно считать, что дополнительные финансовые расходы, связанные с отвлечением средств в НДС, при приобретении материальных ресурсов должны учитываться от момента оплаты до момента расхода ресурсов в производство.

При необходимости использования формулы суммарных затрат условие применения цены с НДС распространяется и на расчёт расходов на содержание страховых запасов с той же предпосылкой, что на их приобретение были выплачены суммы, включающие как номинальную цену, так и НДС. Но затраты на собственно приобр