 |
Главная |
Закон действующих масс
|
из
5.00
|
Закон действующих масс для носителей заряда применим только к равновесным процессам. В любом полупроводнике равновесные концентрации электронов n0 (в зоне проводимости) и дырок p0 (в валентной зоне) можно записать в виде


где f0(ℰ) – функция распределения Ферми-Дирака

Функции плотности состояний gc(ℰ) для зоны проводимости и gv(ℰ) для валентной зоны можно аппроксимировать функциями плотности состояний свободной частицы:


Интегралы в выражениях (1) и (2) берутся соответственно по зоне проводимости и валентной зоне.
Из выражений (1) и (2) следует, что величина n0 и p0 могут трактоваться как площаи областей под кривыми  и
и  на рис.1 заштрихованные области. На рис.1 эти кривые приведены для трех случаев: образец «почти собственного» полупроводника (n0 ≈ p0), образец сильнолегированного полупроводника n–типа (n0 >> p0), образец сильнолегированного полупроводника p–типа (n0 << p0).
на рис.1 заштрихованные области. На рис.1 эти кривые приведены для трех случаев: образец «почти собственного» полупроводника (n0 ≈ p0), образец сильнолегированного полупроводника n–типа (n0 >> p0), образец сильнолегированного полупроводника p–типа (n0 << p0).
Из приведенных графиков видно, что уровень Ферми должен располагаться около середины запрещенной хоны для образцов с проводимостью, близкой к собственной (если бы это было не так, то n0 и p0 не были бы приблизительно равными).

Рис. 1. Распределение электронов и дырок в полупроводнике.
Из аналогичного рассуждения следует, что в образце n-типа уровень Ферми должен быть выше, а в образце p-типа – ниже, чем в образце с почти с собственной проводимостью. Заметим также, что если образец содержит лишь небольшое количество донорных или акцепторных примесей, уровень Ферми должен быть на несколько kT дальше от края ближайшей зоны.
При таких условиях для каждого значения энергии в зоне проводимости 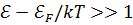 и для каждого значения энергии в валентной зоне
и для каждого значения энергии в валентной зоне  . Это означает, что для зоны проводимости
. Это означает, что для зоны проводимости 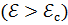

а для валентной зоны

Эти выражения означают, что при описанных выше условиях распределение Ферми – Дирака электронов в зоне проводимости и дырок в валентной зоне можно очень хорошо аппроксимировать распределением Максвелла – Больцмана (6) и (7).
Подставим выражения (4) и (6) в (1) и (5), а (7) в (2). При этом пределы для интеграла по зоне проводимости следует выбрать так: от дна зоны проводимости ℰс до +∞, и для интеграла по валентной зоне – от -∞ до ℰv(потолка валентной зоны). Тогда, соответственно изменяя начало отсчета энергии для n0 и p0, получим выражение

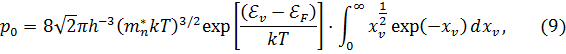
где 
Верхний предел интеграла по зоне проводимости мы взяли равный +∞, а не действительной энергии, соответствующей вершине зоны проводимости; возникающая при этом погрешность невелика, поскольку значение функции распределения  c увеличением ℰ уменьшается так быстро, что в любом случае сколько-нибудь значительный вклад в интеграл дает лишь часть зоны проводимости. Аналогично можно объяснить, почему за нижний предел интеграла для валентной зоны выбрана -∞.
c увеличением ℰ уменьшается так быстро, что в любом случае сколько-нибудь значительный вклад в интеграл дает лишь часть зоны проводимости. Аналогично можно объяснить, почему за нижний предел интеграла для валентной зоны выбрана -∞.
Интегралы в выражениях (8) и (9) можно оценить с помощью таблиц или заметив, что каждый интеграл сводится к гамма-функции 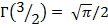 . Подставляя эту величину, можно получить
. Подставляя эту величину, можно получить


где 
Согласно (11), (12) и (13) произведение n0p0 (при фиксированной температуре) имеет постоянное значение
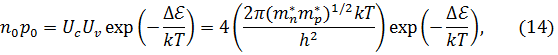
где  ширина запрещенной энергетической зоны между зоной проводимости и валентной зоной. Это и есть закон действующих масс для полупроводников. Заметим, что приближение Больцмана (и, следовательно, закон действующих масс) не выполняется, когда экспоненциальный множитель в (11) или в (12) равен единице или больше, т.е. когда
ширина запрещенной энергетической зоны между зоной проводимости и валентной зоной. Это и есть закон действующих масс для полупроводников. Заметим, что приближение Больцмана (и, следовательно, закон действующих масс) не выполняется, когда экспоненциальный множитель в (11) или в (12) равен единице или больше, т.е. когда  или
или  . В германии и кремнии при комнатной температуре значения Uc и Uv порядка 1019 см3.
. В германии и кремнии при комнатной температуре значения Uc и Uv порядка 1019 см3.
В собственном плупроводнике концентрация n0 и p0 равны. Подставляя  (ni – концентрация электронови дырок собственного полупроводника) в (14), получим
(ni – концентрация электронови дырок собственного полупроводника) в (14), получим

где

Концентрация носителей тока в собственном полупроводнике будет, очевидно, экспоненциальной функцией температуры с энергией активации ∆ℰ/2.
Сульфид кадмия — химическое вещество с формулой CdS.


Рис. 2. Кристаллическая структура. 1) структура сфалерита, 2) вюрцита.
Молярная масса – 144,46 г/моль
Плотность и фаза – 4,82 г/см3, твердое тело
Tпл = 1750 °С
ΔfH°тв = −144 кДж/моль
S°тв = 71 Дж/(K·моль)
ЕС-классификация: токсичен, опасен для окружающей среды.
Сульфид кадмия существует в виде минералов гринокит и хоулиит, которые встречаются в виде жёлтых налетов на сфалерите (ZnS) и смитсоните. На территории бывшего СССР хоулитсодержащие руды встречаются в Алтын-Топкан в Узбекистане. Гринокит, как правило, обнаруживается в ксантохроите в виде рентгеноаморфной разности.[1]Гринокит имеет гексагональную структуру вюрцита. Он имеет желтоватый цвет с удельной массой 4,7 г/см³ и твердостью Мооса 3,8. Хоулиит имеет кубическую структуру сфалерита (цинковой обманки). Так как эти минералы не широко распространены в природе, то для промышленного использования и научно-технических разработок сульфид кадмия получают путем синтеза.
Синтезированные красители кадмия, основанные на сульфиде кадмия, ценятся за их хорошую температурную стабильность во многих полимерах, например, инженерном пластике. С добавлением селена в формулу можно получать цвета красителей в диапазоне от зелёно-жёлтого до красно-фиолетового. Погодное сопротивление для этого красителя равно 8, что показывает устойчивость красителя к ультрафиолету.
Сульфид кадмия является широкозонным полупроводником с шириной запрещённой зоны 2,42 эВ при 300 K. Это свойство CdS, полезное в оптоэлектронике, используется как в фоточувствительных, так и в фотогальванических устройствах. Его используют для изготовления фоторезисторов (приборов, электрическое сопротивление которых меняется в зависимости от освещенности).
Сульфид кадмия действует как люминофор (также в смеси с сульфидом цинка). Монокристаллы сульфида кадмия используются как детекторы элементарных частиц.
|
из
5.00
|
Обсуждение в статье: Закон действующих масс |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

