Приближение сильной связи

Теоретическая часть

Зонная теория твердого тела позволяет с единой квантовомеханической точки зрения объяснить существование металлов, полупроводников и диэлектриков, их электрофизические свойства. В основе зонной теории лежит формирование и заполнение электронами разрешенных и запрещенных энергетических зон с учетом принципа Паули и элементов статистики.

Для определения энергетических состояний электрона в рамках зонной теории твердого тела решается нерелятивистское уравнение Шредингера

Где Ψ(r) – волновая функция электрона.

Точный учет потенциальной энергии кулоновского взаимодействия электрона с электрическим полем кристаллической решетки V(r) приводит к тому, что решение уравнения Шредингера сводится к задаче многих частиц. В результате мы получаем систему уравнений порядка 10²³, решить которую даже современными компьютерными методами невозможно, поэтому для решения этой задачи используют различные приближения. Так, например, адиабатическое приближение основано на том, что масса ядра в атоме много больше массы электрона, поэтому скорость движения ядра уступает примерно на два порядка скорости движения электронов. Это позволяет в первом приближении рассматривать только движение электронов в поле неподвижных ядер. Другое, более распространенное приближение – одноэлектронное, или метод Харти – Фока. В этой модели энергия попарного взаимодействия электронов в кристаллической решетке заменяется взаимодействием одного электрона с усредненным самосогласованным полем всех остальных электронов.

Мы рассмотрим состояние энергии электрона в кристалле – приближения сильной связи.

Приближение сильной связи.

В рамках приближения сильной связи предполагается, что электроны находятся в потенциальных ямах своих атомов (являются квазисвязанными). Если энергия электрона меньше высоты потенциального барьера, то с классической точки зрения такой барьер не проницаем для электрона, а с точки зрения квантовой теории существует вероятность прохождения электрона сквозь потенциальный барьер конечной ширины вследствие туннельного эффекта. Рассмотрим формирование кристалла в рамках приближения сильной связи (рис.1).

Рис.1. Расщепление энергетических уровней при сближении атомов.

Сначала N атомов, расположены далеко друг от друга, а их энергетические уровни 2N–кратно вырождены. При сближении атомов в кристаллическую решетку вырождение энергетических уровней снимается. Дискретные энергетические уровни атомов взаимодействуют друг с другом и расщепляются в энергетические зоны. Взаимодействие между атомами может привести к перекрытию двух отдельных зон, в таком случае получится одна зона с числом электронных состояний равным сумме этих состояний в перекрывшихся зонах. И в этом случае число электронных состояний окажется кратным 2N.

Энергетическая зона или совокупность энергетических зон, образовавшихся в результате расщепления одного или нескольких энергетических уровней изолированных атомов при объединении их в кристаллы, называется разрешенной зоной. К разрешенным зонам относят валентную зону и зону проводимости. На зонных схемах приняты также обозначения дна зоны проводимости – E_C и потолка валентной зоны – E_V (рис.2.2).

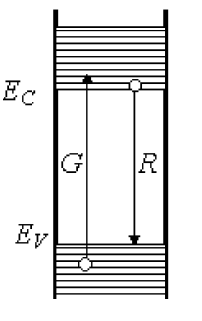
В рамках приближения сильной связи рассматриваются связанные электроны валентной зоны, которые могут, преодолев потенциальный барьер, стать свободными электронами зоны проводимости. Этот процесс называется генерацией свободных носителей заряда (переход G на рис. 2).

В результате таких переходов в валентной зоне появляются свободные энергетические уровни, отсутствие электронов на которых следует трактовать как наличие на них фиктивных зарядов - дырок. Переход электронов из зоны проводимости в валентную зону называется рекомбинацией (переход R на рис. 2). Область значений энергии, которыми не может обладать электрон, называется запрещенной зоной. Ширина запрещенной зоны – это разность энергий между нижним уровнем одной разрешенной зоны и верхним уровнем соседней запрещенной E_g = E_C − E_V . Чем шире запрещенная зона, тем меньше электронов способно преодолеть ее. Высота потенциального барьера соответствует ширине запрещенной зоны. По ширине запрещенной зоны можно провести классификацию твердых тел на металлы, диэлектрики и полупроводники. Если ширина запрещенной зоны E_g > 2÷3 эВ, то твердое тело называется диэлектриком. При абсолютном нуле температуры диэлектрик имеет полностью заполненную валентную зону и пустую зону проводимости. В случае, когда валентная зона заполнена частично, или наблюдается перекрытие зон, при этом запрещенная зона отсутствует E_g → 0, такое твердое тело является металлом. Промежуточное положение занимают полупроводники. Различие между полупроводниками и диэлектриками чисто условное. Можно сказать, что полупроводники – это диэлектрики с E_g < 2 эВ, у которых при низкой температуре все состояния в валентной зоне заполнены электронами.

Практическая часть

Задание

Используя приближение сильной связи, найти собственные значения энергии нижнего края зоны в случае для случая одномерной решетки с периодом π (π/2, π) , если потенциал имеет вид

Предположить, что атомные волновые функции такие, как и у простого гармонического осциллятора,

где – подгоночный параметр выбираем так, чтобы энергия, отвечающая состоянию φ ( x) была минимальной.

Решение

Поскольку потенциал вблизи минимум является параболическим, атомные волновые функции можно аппроксимировать следующим образом:

Интегралы, фигурирующие в расчете, имеют вид

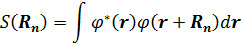
Основные приближения этого метода заключается в том, что мы пренебрегаем всеми , кроме тех, для которых . Пренебрегая при суммировании всеми членами, кроме двух, соответствующих двум соседним ячейками, получаем

Условие минимума величины ℰ как функции дает уравнение уравнение cosπk для каждого значения . Значения ℰ, и k, полученные таким способом, приведены в табл. 1.

Таблица 1

k ℰ

0,674 0,0 -3,463

0,680 0,37 -3,363

0,700 0,502 -3,277

0,750 0,623 -3,163

0,800 0,703 -3,070

0,900 0,925 -2,884

0,910 1,0 -2,870

Заметим, что на границе зоны результаты этого расчета получаются менее точными, чем полученные в [3]. Это объясняется тем, что волновая функция состояния на границе зоны лучше описывается комбинацией волновой функции основного состояния и атомных функций возмущенных состояний, а в нашем разложении последние опущены.

Список литературы

1. О.Ю.Шевченко. Основы физики твердого тела : учебное пособие / СПб., 2010. — 78 с.

2. Г. Дж. Голдсмид. Задачи по физике твердого тела / перевод А.А. Гусева, М.П. Шаскольская – М.: «Наука», 1976. – 432с.

3. Tables relating to Mathieu Functions, Columbia University Press, 1951.