 |
Главная |
Найти указанные пределы
|
из
5.00
|
Примеры решения задач
Задача 1
Найти указанные пределы:
1) 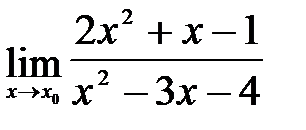 ;
;  ;
;  b)
b) 
2)  ;
;
3)  ;
;
4) 

а) При подстановке вместо переменной  ее предельного значения 2 получаем
ее предельного значения 2 получаем
 =
=  =
= 
б) При подстановке вместо переменной 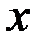 ее предельного значения -1 получается неопределенность вида
ее предельного значения -1 получается неопределенность вида  .
.
 Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой:
Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой:
 где
где  - корни квадратного трехчлена
- корни квадратного трехчлена
 .
.
У нас  , так как дискриминант квадратного трехчлена
, так как дискриминант квадратного трехчлена
 следовательно,
следовательно,  .
.
Аналогично 
Теперь условие примера можно переписать в другом виде и продолжить решение:


b) 
Здесь сталкиваемся с неопределенностью  , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной или предварительно числитель и знаменатель данной дроби разделить на
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной или предварительно числитель и знаменатель данной дроби разделить на  , где n- наивысшая степень числителя и знаменателя.
, где n- наивысшая степень числителя и знаменателя.

Найти пределы:
2) 
3) 
В первом случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из очевидных следствий:
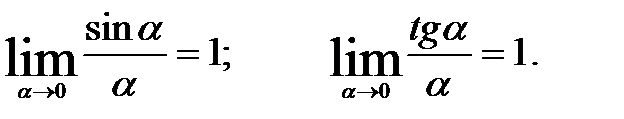
Решение примера будет выглядеть следующим образом:

Во втором случае для освобождения от неопределенности будем использовать второй замечательный предел и одно из очевидных следствий:

Решение примера будет выглядеть следующим образом:
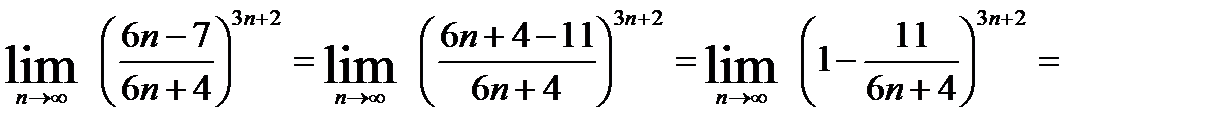


Вычислить:
4) 
Непосредственная подстановка предельного значения аргумента  приводит к неопределенности вида
приводит к неопределенности вида  . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 

Задача 2.
Найти производные  , пользуясь правилами и формулами дифференцирования. При решении всех последующих примеров кроме таблицы производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции.
, пользуясь правилами и формулами дифференцирования. При решении всех последующих примеров кроме таблицы производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции.



г) Если задана сложная функция  где
где  то есть
то есть  если каждая из функций
если каждая из функций  и
и  дифференцируема по своему аргументу, то
дифференцируема по своему аргументу, то 
1) 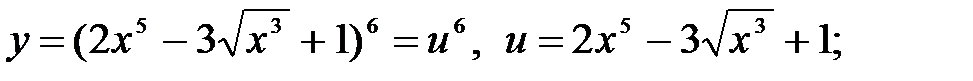


2) 


3) 

4)  ;
;


Задача 3.
Исследовать функцию  методами дифференциального исчисления, начертить их графики. Исследование функций и построение графиков рекомендуется проводить по следующей схеме:
методами дифференциального исчисления, начертить их графики. Исследование функций и построение графиков рекомендуется проводить по следующей схеме:
1) Найти область определения функции 
2) Исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва;
3) найти точки экстремума функции и определить интервалы ее монотонности;
4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;
5) найти асимптоты графика функции;
6) построить график, используя результаты предыдущих исследований;
7) для функции найти наибольшее и наименьшее значения на отрезке 
Решение.
1) Областью определения данной функции являются все действительные значения аргумента  то есть
то есть  =
=  , а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
, а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и интервалы, монотонности. С этой целью найдем ее производную и приравняем к нулю:
 . Решая полученные квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода:
. Решая полученные квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода:  Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума.
Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума.

| 
| 
| 
|  
| 
|
| + | 
| + | ||
| max | min |
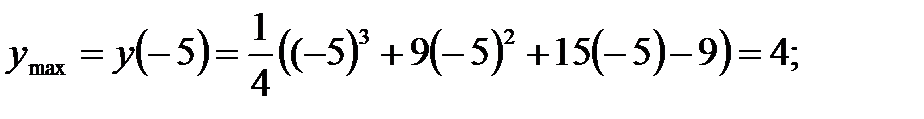

3) Определим точки перегиба графика функции, интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

 ;
;  .
.
Итак, функция имеет одну критическую точку 2 рода 
Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

| 
| 
| 
|

| – | + | |

| Ç | т.п. | È |
Значение  является абсциссой точки перегиба графика функции, а ордината этой точки:
является абсциссой точки перегиба графика функции, а ордината этой точки: 

4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты  воспользуемся формулами:
воспользуемся формулами: 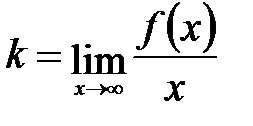 ;
; 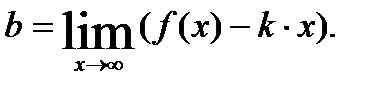

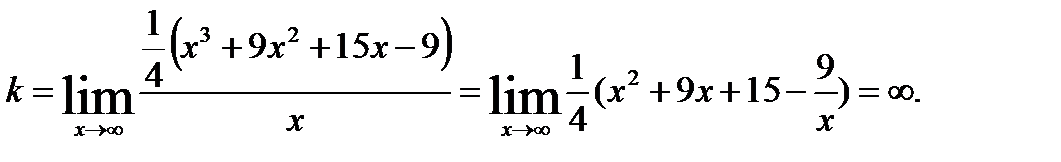
Таким образом, у графика заданной функции наклонных асимптот нет.
5) Для построения графика в выбранной системе координат изобразим точки максимума  , минимума
, минимума  , перегиба
, перегиба  и точки пересечения графика с осью
и точки пересечения графика с осью 
С учетом результатов предыдущих исследований построим кривую.
6) Найдем наибольшее и наименьшее значения заданной функции на отрезке  Для этого посчитаем значения функции на концах этого отрезка, в критических точках 1 рода, попавших на отрезок, и сравним результаты:
Для этого посчитаем значения функции на концах этого отрезка, в критических точках 1 рода, попавших на отрезок, и сравним результаты:

Очевидно, 


Задача 4.
Исследовать следующую функцию и построить схематический график:

1) Область определения:
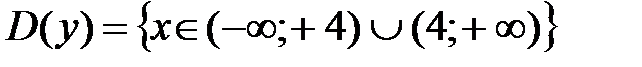
2) Исследование на непрерывность и классификация точек разрыва.
Заданная функция непрерывна всюду, кроме точки 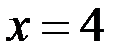 . Вычислим ее односторонние пределы в этой точке:
. Вычислим ее односторонние пределы в этой точке:


Таким образом, точка  является для заданной функции точкой разрыва второго рода, а прямая
является для заданной функции точкой разрыва второго рода, а прямая  -вертикальной асимптотой графика.
-вертикальной асимптотой графика.
3) Исследование на экстремум и промежутки монотонности.


| 
| 
| 
| 
| 
| ||

| + | – | не сущ. | – | + | ||

| max | min |

4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как  то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

| 
| 
| |

| – | не сущ. | + |

| Ç | È |
5) Исследование графика на наличие наклонных асимптот


Таким образом прямая  - наклонная асимптота графика.
- наклонная асимптота графика.
6) Построение графика.
Очевидно, график заданной функции пересекает ось  в точке (0; -5) и на основе обобщения результатов всех предыдущих исследований имеет вид:
в точке (0; -5) и на основе обобщения результатов всех предыдущих исследований имеет вид:

Задача 5.
Среди цилиндров, полная поверхность которых равна  найти
найти
цилиндр, имеющий наибольший объем.
Решение.
Пусть радиус основания цилиндра равен  а высота равна
а высота равна  .Тогда
.Тогда
 откуда
откуда  то есть объем цилиндра может быть выражен следующим образом:
то есть объем цилиндра может быть выражен следующим образом:
 .
.
Исследуем полученную функцию на максимум при 

Имеем  при
при  по условию задачи
по условию задачи  .
.
Так как при  выполняется условие
выполняется условие  то объем имеет наибольшее значение. При этом
то объем имеет наибольшее значение. При этом  поэтому искомые значения радиуса основания и высоты цилиндра равны соответственно 1 и 2.
поэтому искомые значения радиуса основания и высоты цилиндра равны соответственно 1 и 2.
Задача 6.
Следующая формула используется для вычислений приближенных значений функций:

Вычислить приближенно 

Решение.
Рассмотрим функцию 
По формуле имеем:  т.е.
т.е.

Так как  то при
то при 
и  получаем:
получаем:

Можно показать, что абсолютная погрешность формулы не превышает величины  где
где  наибольшее значение
наибольшее значение  на сегменте
на сегменте 
Задача 7.
Найти наибольшее и наименьшее значения функции  на
на
отрезке 
Решение.
Находим критические точки данной функции:
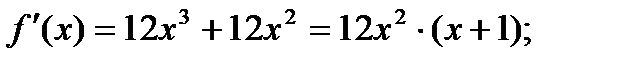
 при
при  и при
и при  Находим
Находим 


 Итак,
Итак,  в точке
в точке 
 в точке
в точке 
Расчетные задания
Задание № 1
Найти указанные пределы
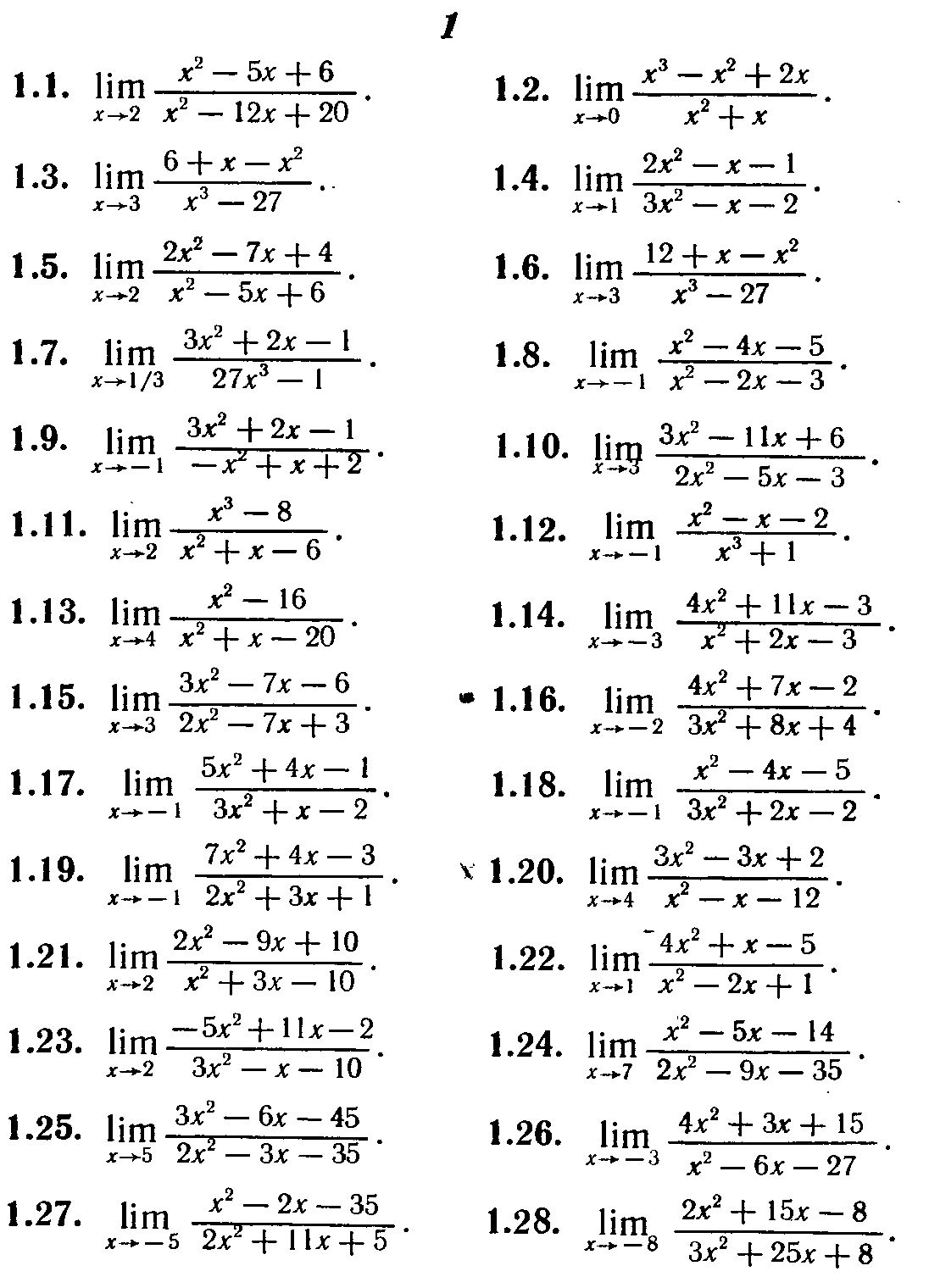
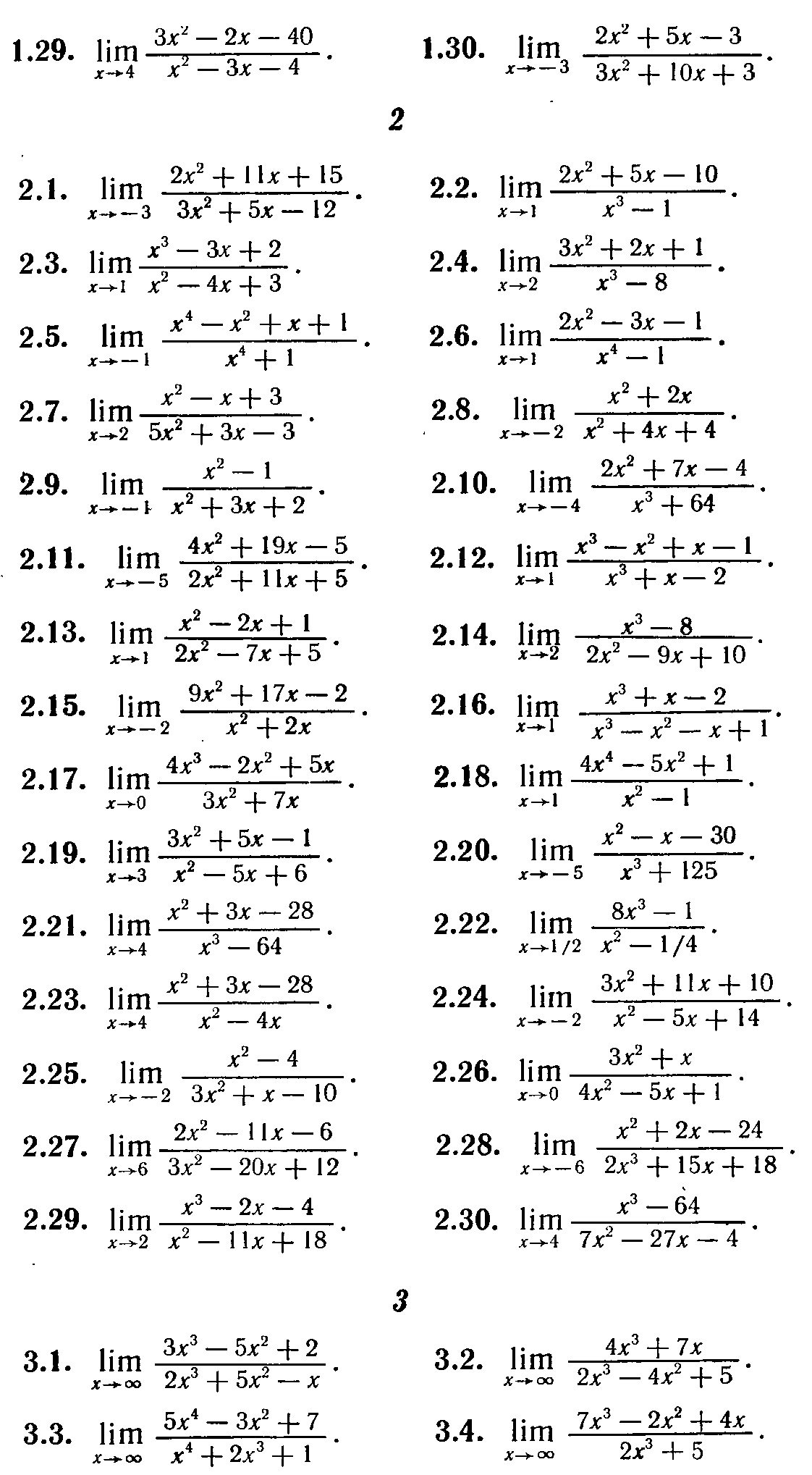
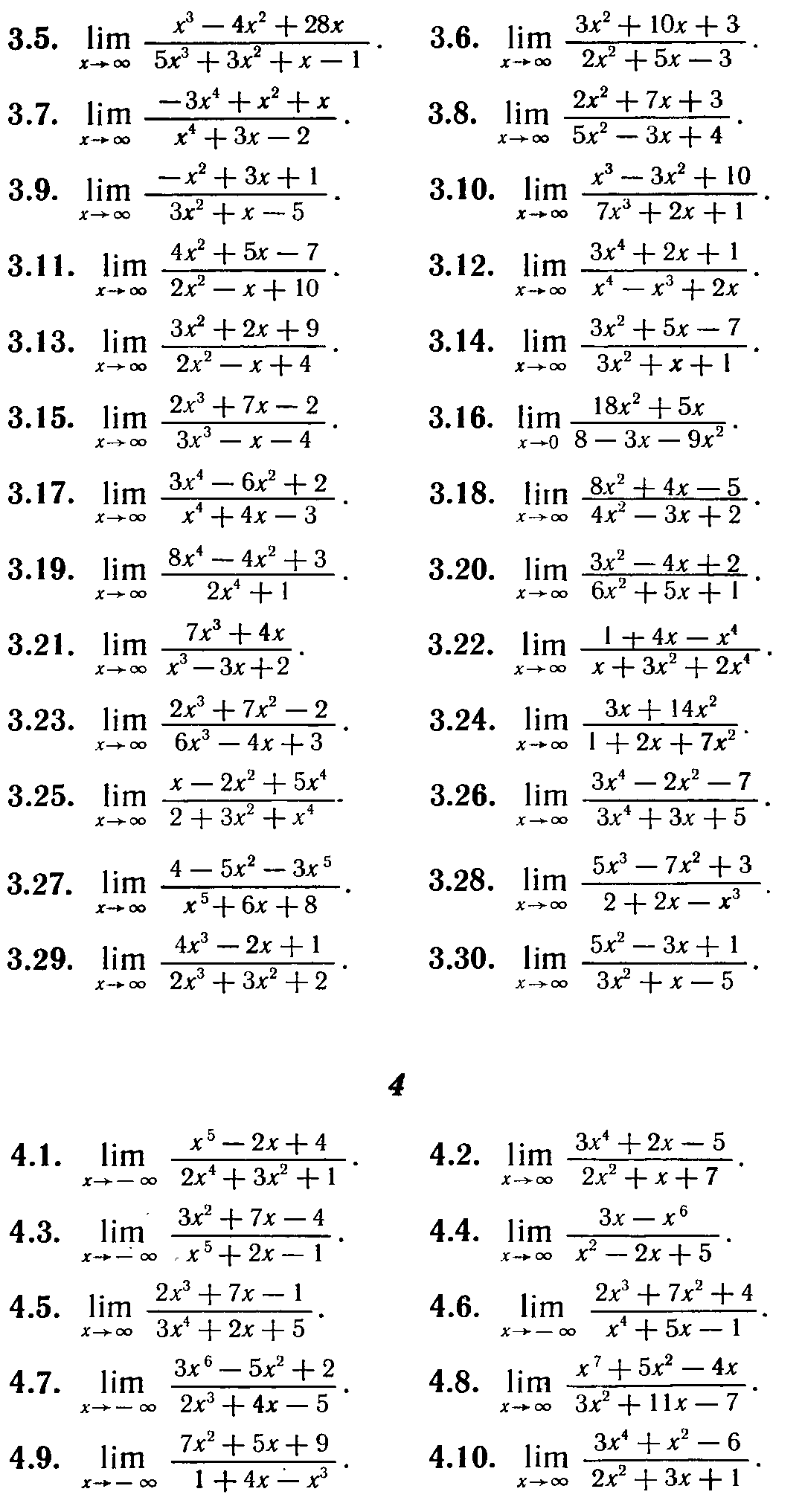
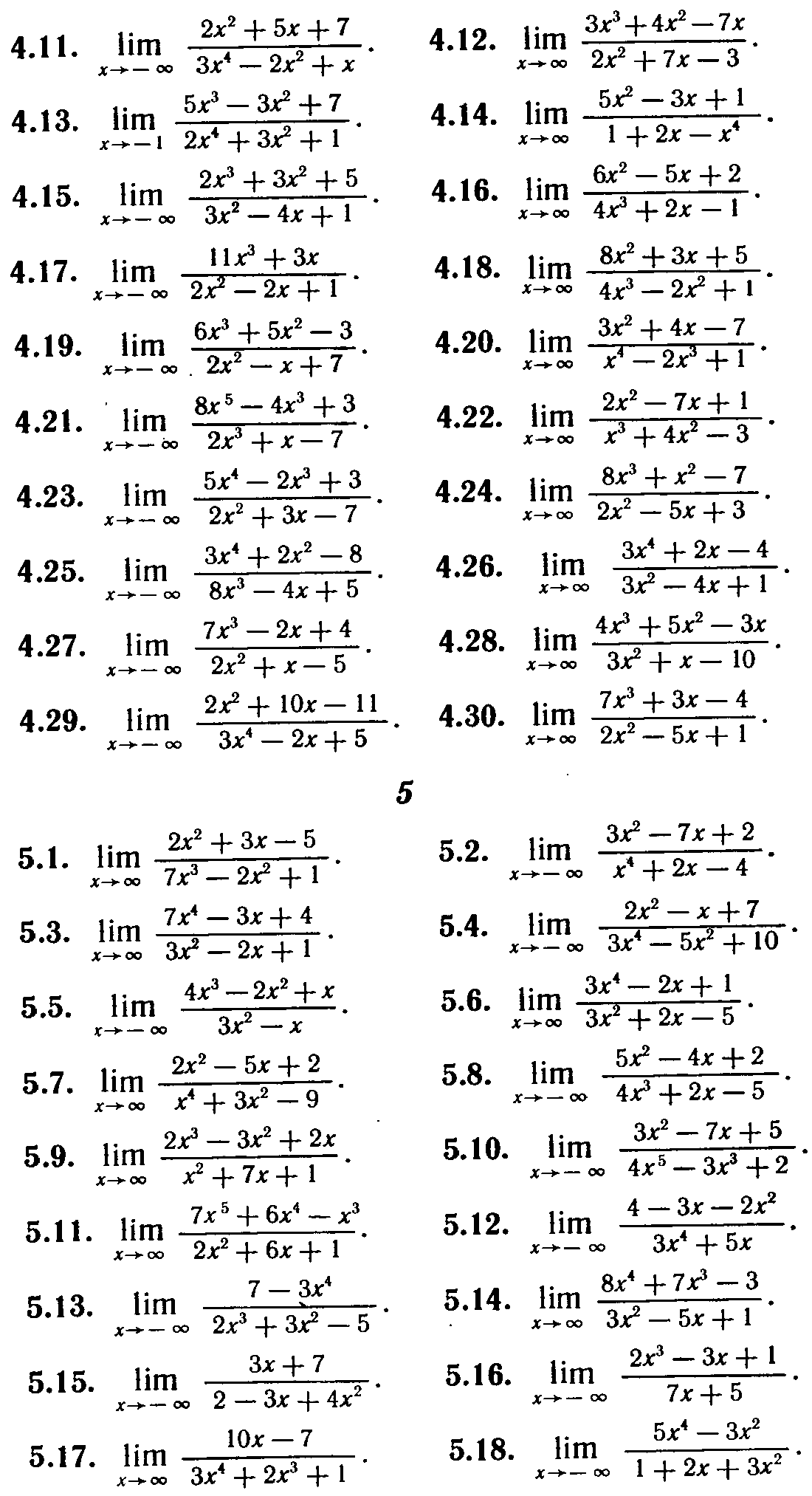






Задание 2


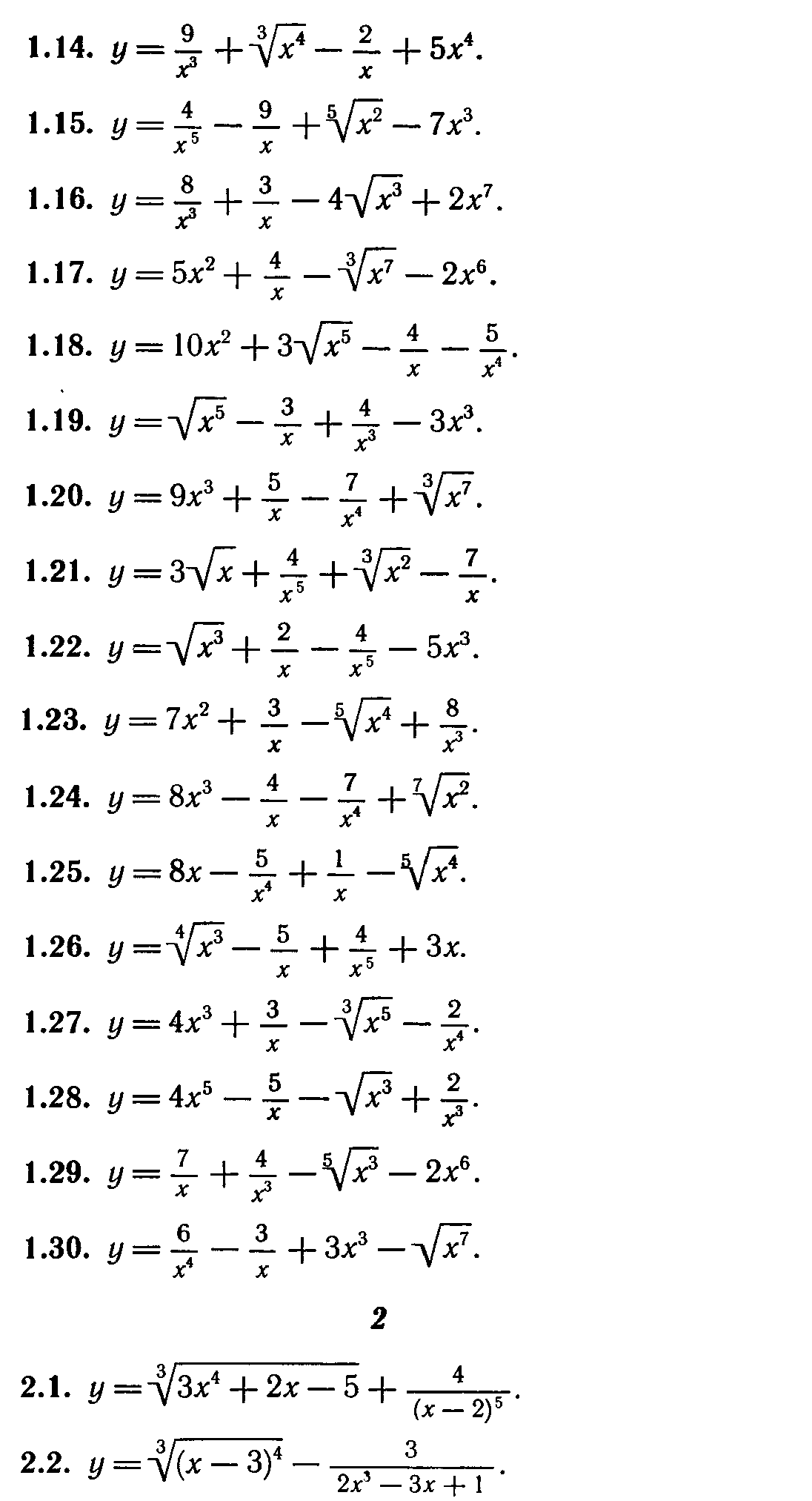











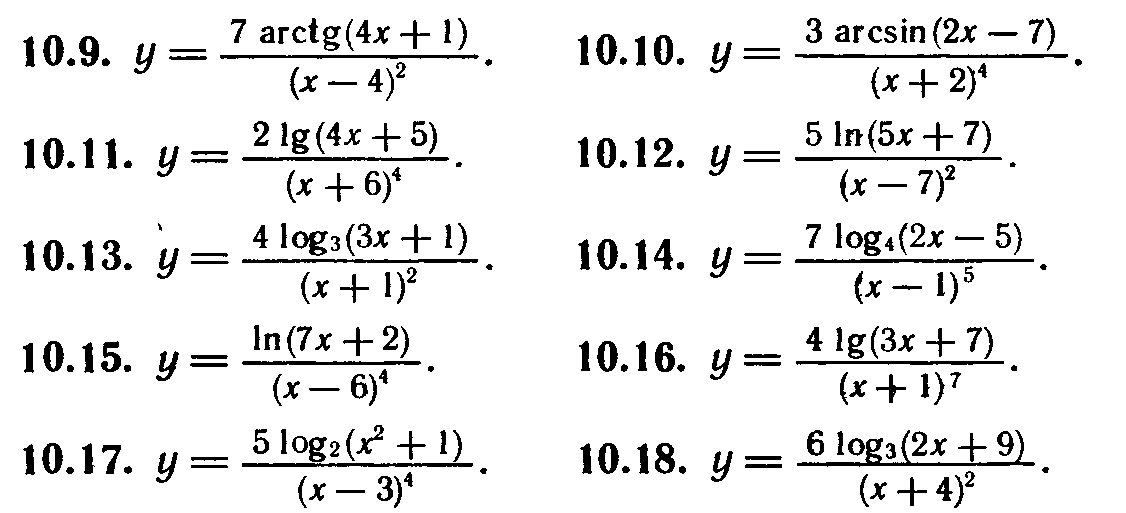

Задание 3


Задание 4



Задание 5


Задание 6








|
из
5.00
|
Обсуждение в статье: Найти указанные пределы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

