Примеры расчёта чисел зубьев

ПРИЛОЖЕНИЕ 1.9.1

 

Рассчитать число зубьев для варианта , знаменатель ряда равен .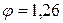

По графику частот вращения шпинделя (рис.1.а) определяем все передаточные отношения и наносим их на график чисел оборотов (рис.1.б)

Передаточные отношения передач первой и второй групп:

Подставляя знаменатель ряда в полученные выражения, представляем передаточные отношения в виде обыкновенных дробей:

Убеждаемся. что найденная нами величина передаточного отношения лежит в пределах , если значение выхолит за границы данного интервала, то график частот вращения необходимо откорректировать.

После определения всех передаточных отношений зубчатых передач, переходим к расчёту чисел зубьев колёс методом наименьшего общего кратного.

Для этого, как описано в п.3.4, по формуле (3.12) записываем суммы:

Наименьшее общее кратное:

Проверяем, чтобы , в противном случае необходимо уменьшить число всех зубьев, путём деления их на одинаковое число. При этом получаются дробные значения чисел зубьев, и их требуется округлить.

Найдя наименьшее общее кратное , подставляем его в уравнение (3.11)

Вычисляем числа зубьев:

Полученные значения чисел зубьев оказались меньше допустимого , поэтому, их необходимо увеличить в несколько раз. Помножим каждое из чисел зубьев первой группы на 3, а второй на 10, тогда получим:

Если число зубьев мало 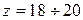, то зубчатое колесо выполняют вместе с валом (вал-шестерня).

В итоге получились конечные числа зубьев зубчатых прямозубых колёс, которые для привода главного движения удовлетворяют условию минимального числа зубьев зубчатых колёс , а их передаточное отношение лежит в допустимых пределах .

 

 

ПРИЛОЖЕНИЕ 1.9.2

 

Рассчитать число зубьев для варианта 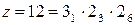, знаменатель ряда равен .

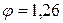По графику частот вращения шпинделя (рис.2.а) определяем все передаточные отношения и наносим их на график чисел оборотов (рис.2.б). Передаточные отношения передач первой, второй и третей групп:

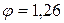Так как, знаменатель ряда в нашем случае равен , то подставляя его в полученные выражения, представляем передаточные отношения в виде обыкновенных дробей, имеем:

Убеждаемся, что найденная нами величина передаточного отношения лежит в пределах , если значение выходит за границы данного интервала, то график частот вращения необходимо откорректировать.

После определения всех передаточных отношений зубчатых передач, переходим к расчёту чисел зубьев колёс методом наименьшего общего кратного.

Для этого, как описано в п.3.4, по формуле (3.12) находим суммы:

Наименьшее общее кратное:

Проверяем, чтобы , в противном случае необходимо уменьшить число всех зубьев, путём деления их на одинаковое число. При этом получаются дробные значения чисел зубьев, и их требуется округлить.

Найдя наименьшее общее кратное , подставляем его в уравнение (3.11) Вычисляем числа зубьев:

Полученные значения чисел зубьев оказались меньше допустимого , поэтому, их необходимо увеличить в несколько раз. Помножим каждое из чисел зубьев первой группы на 3, второй на 10 и третей на 9, тогда получим:

Полученные значения чисел зубьев удовлетворяют условию минимального числа зубьев зубчатых прямозубых колёс привода главного движения и являются конечным результатом расчёта чисел зубьев.

 

 

ПРИЛОЖЕНИЕ 1.9.3

 

Рассчитать число зубьев для варианта с многоскоростным электродвигателем , знаменатель ряда равен 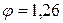(т.к. 1,26³=2).

По графику частот вращения шпинделя (рис.3.а) определяем все передаточные отношения и наносим их на график чисел оборотов (рис.3.б)

Передаточные отношения передач первой и второй групп:

Подставляя в полученные выражения, представляем передаточные отношения в виде обыкновенных дробей, имеем:

Убеждаемся, что найденная нами величина передаточного отношения лежит в пределах , если значение выходит за границы данного интервала, то график частот вращения необходимо откорректировать.

После определения всех передаточных отношений зубчатых передач, переходим к расчёту чисел зубьев колёс методом наименьшего общего кратного.

Для этого, как описано в п.3.4, по формуле (3.12) записываем суммы:

Наименьшее общее кратное:

Проверяем, чтобы , в противном случае необходимо уменьшить число всех зубьев, путём деления их на одинаковое число. При этом получаются дробные значения чисел зубьев, и их требуется округлить.

Найдя наименьшее общее кратное , подставляем его в уравнение (3.11)

Вычисляем предварительные числа зубьев:

Полученные значения чисел зубьев первой группы, оказались меньше допустимого , поэтому, их необходимо увеличить в несколько раз. Помножим каждое из чисел зубьев первой группы на 3, тогда получим:

В итоге получились конечные числа зубьев зубчатых прямозубых колёс, которые для привода главного движения удовлетворяют условию минимального числа зубьев зубчатых колёс , а их передаточное отношение лежит в допустимых пределах .

 

ПРИЛОЖЕНИЕ 2

 

Проектировочный расчет модуля зубчатых колес

 

ПРИЛОЖЕНИЕ 2.1

Параметр, учитывающий отношение ширины зубчатого венца к диаметру

 

Ориентировочно, при консольном расположении колеса относительно опор y_bd = (0,3-0,4)/(0,2-0,25); при несимметричном расположении относительно опор y_bd = (0,6 -1.2)/(0,3-0,6), при симметричном –y_bd = (0,8-1.4)/(*0,4-0,9); В числителе - при НВ ≤ 350; взнаменателе-при НВ≥350. Подробнее см .(9 стр.266)

 

 

ПРИЛОЖЕНИЕ 2.2

Коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца - K_Fb [3 с. 596]

 

 

 

Рис 4. График для определения ориентировочных значений коэффициента K_Fb;

где: кривые 1-7 соответствуют передачам,указанным на верхней схеме;

 

ПРИЛОЖЕНИЕ 2.3

Графики для определения – коэффициента, учитывающего форму зуба

 

– коэффициент, учитывающий форму зуба, определяется в зависимости от эквивалентного числа зубьев, величины смещения исходного контура и формы зуба, см. [3, с.588], определяется по рисунку:

 

 

Рис 5. Графики для определения – коэффициента, учитывающего форму зуба

 

Где: Х- коэффициент смещения исходного контура ( приближенно принимают Х=0)

– эквивалентное число зубьев,

– угол наклона зубев, 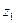– число зубьев шестерни

м/с – окружная скорость

z₁ – число зубьев шестерни, т. е. наименьшего колеса в руппе;

– эквивалентное число зубьев;

– угол наклона зубев (для прямозубых колес =0), 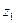– число зубьев шестерни;

Например, при 30 и Х=0 коэффициент, учитывающий форму зуба =3.8

 

 

ПРИЛОЖЕНИЕ 2.4

– коэффициент долговечности

 

При определенеии полученное значение должно быть меньше 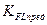, при , при . В противном случае следует принимать . Если окажется, что , то . (9стр.282). Где -для зубчатых колес с твердостью поверхности зубьев НВ ≤ 350, для зубчатых колес, закаленных при нагреве т.в.ч. с обрывом закаленного слоя у переходной поверхности, и зубчатых колес со шлифованной переходной поверхностью вне зависимости от твердости и термообработки их зубьев; - для зубчатых колес с нешлифованной поверхностью при ее твердости НВ≥350 .

 

ПРИЛОЖЕНИЕ 3

Габаритные размеры подшипников лёгкой серии.

 

Обозначение подшипников	d	D	B	r	Шарики	Масса, кг	С,Н	С0,Н	n пред* 10-3мин-1
DW	z
Легкая серия диаметров 2, укая серия ширин 0
				0.3	1.59		0.0016
				0.4	2.38		0.003
				0.5	3.18		0.003
				0.5	3.97		0.008
				0.5	3.97		0.013
				1.0	4.76		0.019
				1.0	5.95		0.030
				1.0	5.56		0.037
				1.0	5.95		0.045
				1.0	7.14		0.060
				1.5	7.94		0.10
				1.5	7.94		0.12
				1.5	9.53		0.20
				2.0	11.11		0.29
				2.0	12.7		0.36
				2.0	12.7		0.41
				2.0	12.7		0.47			7.3
				2.5	14.29		0.60			6.6
				2.5	15.88		0.80			6.5
				2.5	16.67		0.98			5.4
				2.5	17.46		1.08			5.3
				2.5	17.46		1.18			4.5
				3.0	19.05		1.40			4.6
				3.0	19.84		1.80			4.3
				3.0	2.23		2.2			3.3
				3.5	25.4		3.2			3.4

 

 

ПРИЛОЖЕНИЕ 4

Пример расчета вала

Пример расчёта вала по справочнику Анурьева [3, c.27-29].
ПРИЛОЖЕНИЕ 5

Таблица №4

Основные технические характеристики электродвигателей.

 

 

 

Таблица №5

 

ПРИЛОЖЕНИЕ 6