 |
Главная |
Разложение функции в степенной ряд
|
из
5.00
|
Числовые ряды. Основные понятия
| № п/п | Понятие | Определение и обозначение | ||
| 1. | Ряд | 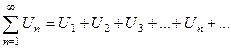
| ||
| 2. | Члены ряда, общий ( n – ый ) член ряда |  - бесконечная числовая последовательность, где - бесконечная числовая последовательность, где 
| ||
| 3. | Частичные суммы ряда | 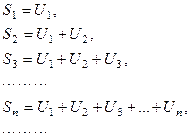
| ||
| 4. | Последовательность частичных сумм | 
| ||
| 5. | Сходящиеся ряды |  , где , где  – сумма ряда – сумма ряда 
| ||
| 6. | Расходящиеся ряды | 
| ||
| 7. | Остаток ряда | 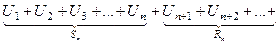

| ||
| Основные свойства сходящихся рядов | ||||
 сходится сходится
| 
| 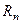 - сходится - сходится
| ||
 сходится, сходится,  – его сумма – его сумма
| 
|  сходится, сходится,  - его сумма - его сумма
| ||
 сходится, сходится,  – его сумма – его сумма
| 
| 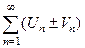 - сходится - сходится
| ||
 сходится, сходится,  – его сумма – его сумма
| 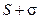 - его сумма - его сумма
| |||
| Необходимый признак сходимости ряда | ||||
 - сходится - сходится
| 
| 
| ||
Замечание: 
| 
|  - расходится - расходится
| ||
Числовые ряды с положительными членами
Определение   - действительные числа - действительные числа
| ||||||||
| Некоторые ряды и их поведение | Гармонический ряд  расходится расходится
| |||||||
Обобщенный гармонический ряд  при при  
| ||||||||
| Ряд геометрический |  при при 
| |||||||
В частности при 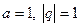 ряды ряды
|  расходится расходится
| |||||||
| Достаточные признаки сходимости числовых рядов с положительными членами | ||||||||
| Признаки сравнения | Интегральный признак Коши | Признак Даламбера | Признак Коши | |||||
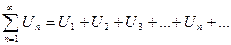 (1) (1)
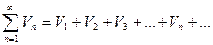 (2) (2)
|  , , 
 : непрерывная, положительная, невозрастающая : непрерывная, положительная, невозрастающая 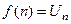
 Замечание:
Замечание:
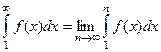
| 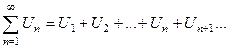
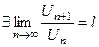
| 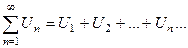

| |||||
1. 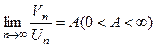 где
где  , ,  (при
(при  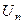 ~ ~  ) )
| Þ |  и и  одновременно сходятся или расходятся
одновременно сходятся или расходятся
| а) 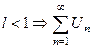 - сход.
б) - сход.
б) 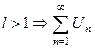 - расход. - расход.
| а) 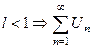 - сход.
б) - сход.
б) 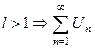 - расход. - расход.
| ||||
2. а)  сход. сход.
| Þ |  сход сход
| Замечание:
1. Если  , то признак Даламбера и Коши не дают ответа о поведении ряда.
2. Признак Даламбера иногда используется без предельного перехода: , то признак Даламбера и Коши не дают ответа о поведении ряда.
2. Признак Даламбера иногда используется без предельного перехода:
 сход., сход.,  расход. расход.
| |||||
б)  расход. расход.
| Þ |  расход. расход.
| ||||||
Замечание: В качестве рядов для сравнения удобно выбирать ряды  и и 
| ||||||||
Знакопеременные числовые ряды
| Определение |  , ,  - действительные числа произвольного признака
В частности, - действительные числа произвольного признака
В частности, 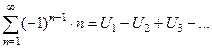 , ,  - знакочередующийся ряд - знакочередующийся ряд
| |||
| Абсолютная и условная сходимость знакопеременных рядов | 1.  и и  сходятся сходятся   - абсолютно сходится
2. - абсолютно сходится
2.  сходится, а сходится, а  расходится расходится   - условно сходится - условно сходится
| |||
| Достаточные признаки сходимости знакопеременных рядов | ||||
| Признак абсолютной сходимости | Признак Лейбница | |||
 - знакопеременный - знакопеременный
 сходится сходится   абсолютно сходится абсолютно сходится
| 1) 
|  сходится сходится
| ||
2) 
| Þ | 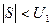
| ||
3) 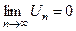
| 
| |||
Замечание:
1. В сходящемся знакочередующемся ряде  сумма S может быть заменена сумма S может быть заменена 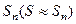 . Получаемая погрешность . Получаемая погрешность  2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если
2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если  с некоторого номера, то члены ряда с некоторого номера, то члены ряда  убывают с этого номера.
3. Если расходимость ряда убывают с этого номера.
3. Если расходимость ряда  установлена признаком Даламбера или признаком Коши, то и ряд установлена признаком Даламбера или признаком Коши, то и ряд  расходится, т. к. если расходится, т. к. если  или или  , то , то  . .
| ||||
Алгоритм исследования знакопеременного ряда  на сходимость. на сходимость.
| ||||
1. Составить ряд из абсолютных членов данного ряда  и исследовать его сходимость.
2. а) и исследовать его сходимость.
2. а)  сходится сходится   абсолютно сходится; б) абсолютно сходится; б)  расходится расходится  3 исследуй
3. Проверить условия признака Лейбница
Если 1) члены чередуются по знаку;
2) 3 исследуй
3. Проверить условия признака Лейбница
Если 1) члены чередуются по знаку;
2)  3)
3)  то 1) то 1)  сходится по признаку Лейбница
2) сходится по признаку Лейбница
2)  условно сходится, т. к. условно сходится, т. к.  расходится расходится
| ||||
Функциональные ряды. Основные понятия
| Понятие | Определение и обозначение | ||||
| 1. Функциональный ряд | 
| ||||
| 2. Члены ряда | 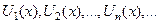 - функции от - функции от 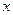
| ||||
3. Сходимость ряда в точке 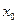
|  сходится сходится   сходится в т. сходится в т. 
 расходится расходится   расходится в т. расходится в т. 
| ||||
| 4. Область сходимости ряда |  сходится сходится  - область сходимости; - область сходимости;  - находится: - находится:
 или или  , ,
| ||||
| 5. Последовательность частичных сумм | 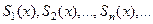 , где , где
 , , 
| ||||
| 6. Сумма сходящегося ряда |  - сумма ряда - сумма ряда
| ||||
| 7. Остаток ряда | 
| ||||
8. Равномерная сходимость ряда  на на 
|  и и 
| ||||
| 9. Абсолютная и равномерная сходимость ряда (признак Вейерштрасса) | 1.  и и  2. числовой ряд
2. числовой ряд  - сходится - сходится
| Þ |  - сходится абсолютно и равномерно на - сходится абсолютно и равномерно на 
| ||
| Свойства равномерно сходящихся рядов | |||||
1.  - равномерно сходится на - равномерно сходится на  2.
2. 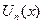 - непрерывна - непрерывна  и и  3.
3.  - его сумма - его сумма 
| Þ | 1.  - непрерывна на - непрерывна на  2.
2. 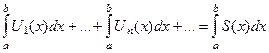 , где , где  (почленное интегрирование)
3. (почленное интегрирование)
3.  - равномерно сходится на - равномерно сходится на  , где , где 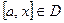
| |||
1.  - сходится на - сходится на  , ,  - его сумма
2. - его сумма
2. 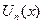 - дифференцируемые - дифференцируемые  и и 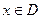 3.
3.  - непрерывны - непрерывны  и и 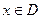 4.
4.  - равномерно сходится на - равномерно сходится на 
| Þ | 1.  - равномерно сходится на - равномерно сходится на  2.
2.  (почленное дифференцирование)
(почленное дифференцирование)
| |||
Степенные ряды
| Определение и обозначение | (1) 
|
(2)  , где , где  - постоянные коэффициенты - постоянные коэффициенты
| |
| Радиус сходимости. Основная теорема | Для рядов (1) и (2)  число число  , обладающие свойствами, , обладающие свойствами,  - радиус сходимости - радиус сходимости
|
1)  при при 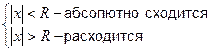
| 
|
2)  при при 
| 
|
| Свойства степенных рядов | 1. 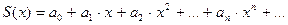 , ,  - непрерывна - непрерывна  2.
2. 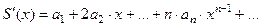 - сходится - сходится  3.
3.  - сходится - сходится 
|
| Алгоритм определения интервала сходимости | 1.Найти  или или  2.Решить неравенство
2.Решить неравенство  , получить интервал сходности , получить интервал сходности  3.Исследовать сходимость ряда на концах полученного интервала
3.Исследовать сходимость ряда на концах полученного интервала
|
Разложение функции в степенной ряд
Ряд Тейлора (по степеням  ) )
| 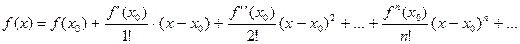
|
Ряд Маклорена (по степеням 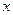 ) )
| 
|
| Алгоритм разложения функции в степенной ряд. | 1. Найти все производные 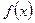 в точке в точке 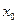 : :
 2. записать ряд Тейлора для
2. записать ряд Тейлора для 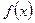 : :  3. Найти интервал сходимости
3. Найти интервал сходимости  полученного ряда
4. Найти полученного ряда
4. Найти  , где , где  - остаточный член формулы Тейлора - остаточный член формулы Тейлора  5. Если
5. Если 
|
Таблица разложений некоторых функций в степенные ряды
| № п/п | Функция | Разложение в ряд | Интервал сходимости |

| 
| 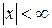
| |

| 
| 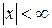
| |

| 
| 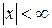
| |

| 
| 
| |

| 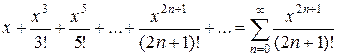
| 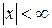
| |

| 
| 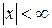
| |

| 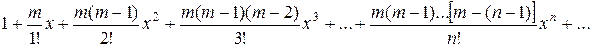
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
|
|
из
5.00
|
Обсуждение в статье: Разложение функции в степенной ряд |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Популярное:
Генезис конфликтологии как науки в древней Греции: Для уяснения предыстории конфликтологии существенное значение имеет обращение к античной...
Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы...

©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (357)
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

