Определение усилий в стержнях простейших ферм

ПЛОСКИЕ ФЕРМЫ.

Понятие о ферме. Классификация ферм.

Фермой называется стержневая система, остающаяся геометри­чески неизменяемой после условной замены ее жестких узлов шар­нирными. Если в узлах фермы приложены сосредоточенные нагрузки, то стержни фермы работают главным образом на центральное сжатие или растяжение.

Кроме плоских ферм, у которых оси всех стержней расположены в одной плоскости, применяются пространственные фермы, оси эле­ментов которых не лежат в одной плоскости. Расчет про­странственной фермы во многих случаях удается свести к расчету нескольких плоских ферм.

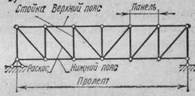Расстояние между осями опор фермы называется пролетом. Стержни, расположенные по внешнему контуру фермы называются поясными и образуют пояса; стержни, соединяющие поя­са, образуют решетку фермы и называются: вертикальные — стой­ками, наклонные — раскосами. Расстояние между соседними

Рис 1. узла­ми любого пояса фермы (обычно измеряемое по горизонтали) называется панелью (рис.1).

Классификацию ферм прове­дем по следующим пяти призна­кам: 1) характеру очертания внешнего контура;

2) типу решет­ки;

3) типу опирания фермы;

4) назначению фермы;

5) уровню езды.

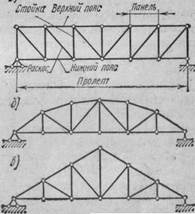
По характеру очер­тания различают фермы с па­раллельными поясами (рис.2.а) и с ломаным или так называе­мым полигональным расположе­нием поясов. К последним от­
носятся фермы с па раболическим очертанием верхнего пояса (рис.2.б) и фермы треугольного очертания (рис.2.в).

По типу решетки фермы делятся на: Рис. 2.

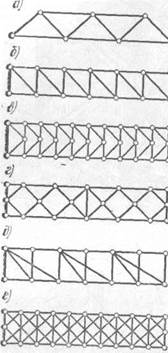
фермы с треуголь­ной решеткой (рис.3.а);

фермы с раскосной решеткой (рис.3.б),фермы с полураскосной решеткой (рис.3.в), фермы с ромбической решеткой (рис.3.г), двухрешетчатые (рис.3.д), многорешетчатые (рис.3.е)

По типу опирания фермы могут быть: : закрепленными у обоих концов — балочными (рис.а) или арочными (рис. д, е); консольными — закрепленными у одного конца (б); балочно-консольными (рис. в, г).

В зависимости от назначения различают фермы стропильные(рис. 4, а), крановые (рис. 4,б), башенные (рис. 4, в), мостовые(рис.5) и др.

Мостовые фермы в зависимости от

Рис.3. уровня езды делятся на фермы с ездой

понизу (рис. 5, а), фермы с ездой поверху, (риг. 5, б) и фермы с ездой посередине (рис. 5, в).

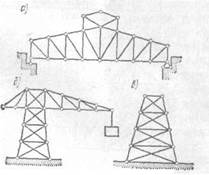
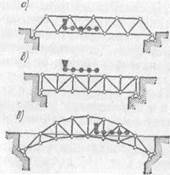
Рис 4 Рис.5

Определение усилий в стержнях простейших ферм.

Фермы, образованные из шарнирного треугольника путем последовательного присоединения узлов (причем каждого с помощью двух стержней, не лежащих на одной прямой), называются простейшими. Такие фермы геометрически неизменяемы и статически определимы.

Для любой статически определимой фер­мы можно составить 2К уравнений статики (где К — число узлов фермы), с помощью которых можно найти опорные реакции и внут­ренние усилия (продольные силы) в ее стержнях от действия внеш­ней нагрузки. При этом в первую очередь обычно определяют опор­ные реакции. При определении реакций составляют три уравнения равновесия для всей фермы в целом.

Для определения внутренних усилий следует выделять сечения­ми узлы или отдельные части фермы и рассматривать условия их равновесия под действием внешних нагрузок и усилий в рассечен­ных стержнях. Всего можно составить (2К—3) таких условий (т. е. независимых друг от друга уравнений).

Выделение узлов или частей фермы необходимо производить так, чтобы усилия в элементах фермы определялись наиболее прос­то, по возможности без совместного решения системы уравнений со многими неизвестными. Это позволяет не только значительно упрос­тить расчет, но и получить более точные результаты.

Рассмотрим способы расчета, позволяющие определить внутреннее усилие в каждом из элементов фермы, как правило, с помощью одного уравнения с одним неизвестным.

Способ моментной точки. Способ моментной точки применяется главным образом в тех случаях, когда удается рассечь ферму на две части так, чтобы при этом перерезанными оказались три ее стержня, направления осей которых не пересекаются в одной точке (см., на­пример, сечение /—/ на рис. 6, слева). Направления осей трех таких перерезанных стержней пересекаются попарно в трех точ­ках, не лежащих на одной прямой (рис. 6. справа).

Рис 6.

Составляя последовательно уравнения моментов всех сил (внеш­них и внутренних), действующих на отсеченную часть фермы, относительно этих трех точек, будем каждый раз получать уравнение с одним неизвестным, представляющим собой усилие в рассеченном стержне, не проходящем через рассматриваемую точку пересече­ния стержней.

Таким образом, для определения усилия в каком-либо стержне необходимо разрезать ферму так, чтобы в разрез кроме данного стержня попали еще два других (оси которых не сходятся с ним в общей точке), после чего из уравнения моментов относительно точки пересечения осей этих двух стержней можно легко определить усилие в данном стержне.

Точка пересечения осей двух стержней, относительно которой составляется уравнение моментов, называется моментной.

При составлении уравнений равновесия все неизвестные усилия в стержне фермы условно считаются положительными, т. е. растя­гивающими и, следовательно, направленными от узлов. Если после решения уравнений какое-либо усилие окажется отрицательным, то, значит, оно является сжимающим и направлено к узлу.

Способ проекций.Способ проекций применяется главным образом в следую­щих двух вариантах:

1) рассматривается равновесие части фермы (как и при способе моментной точки), когда два из трех рассеченных стержней параллельны друг другу;

3) рассматривается равновесие выде­ляемых из фермы узлов (способ выре­зания узлов).

Определим усилия в элементах решетки фермы, изображенной на рис. 7.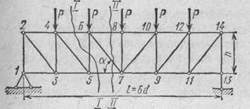

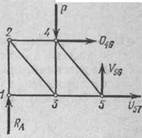
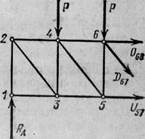
Рис.7. Рис.8. Рис.9.

Для определения усилия V₅₆ разрежем ферму сечением /—/, пересекающим стержни 4—6, 5—6 и 5—7. Так как моментная точка для усилия V₅₆ вследствие параллельности стержней 4—6 и 5—7 находится в бесконечности, то составить уравнение моментов от­носительно этой точки невозможно. Поэтому составим условие рав­новесия в виде суммы проекций всех сил, действующих на отсечен­ную часть фермы (рис. 8), на ось, перпендикулярную ее поясам (в это уравнение усилия в поясах не войдут, так как они перпендикулярны оси проекций:

где Q — поперечная сила в простой балке.

Для определения усилия D₆₇ разрежем ферму по линии II—II (см. рис. 7) и составим уравнение равновесия для левой ее части (рис. 9):

ΣY=R _A—P—P—D₆₇sin α=0, откуда

D_e7=(R_A—2P)/ sin α =Q/sin a,

где Q — поперечная сила в простой балке, равная R_A—2Р.

При расчете простейших ферм все усилия можно определить способом проекций, применяя его последовательно к каждому узлу. При этом определение усилий надо начинать с узла, в котором схо­дится не более двух стержней.

Для примера определим усилия в стержнях 1—2, 1—3, 2—3 и 3—5 фермы, изображенной на рис. 10. Вырежем сначала левый опорный узел (рис. 11) и рассмотрим условия его равновесия.

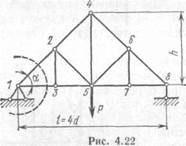
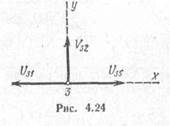
Рис10. Рис.11 Рис.12.

Для определения усилия О₁₂ спроецируем все силы, действую­щие на узел, на ось, перпендикулярную направлению стержня 1—3, т. е. на вертикальную ось y:

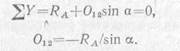
В данном случае R_A равно Р/2, а потому

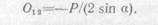
Для определения усилия U₁₃ спроецируем все силы, действую­щие на опорный узел, на ось, перпендикулярную направлению стержня 1—2, т. е. на ось у₁:

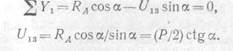
Отметим, что усилие в стержне 1—3 можно было определить и из уравнения проекций всех сил на ось х:

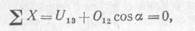
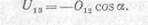
Подставив в последнее уравнение значение усилия О₁₂ найдем

Для определения усилий в стержнях 3—2 и 3—5 вырежем узел 3 и рассмотрим условия его равновесия (рис. 12). Составим сумму проекций сил на ось х:

Откуда (учитывая, что через U₁₃ и U₃₁ обозначено одно и то же усилие, а именно усилие в стержне , соединяющем узлы 1-3), получим:

Спроецировав все силы на вертикальную ось у, получим:

Усилие в стержне 3—2 было бы также равно нулю, если этот стержень и не был бы перпендикулярен стержням 1—3 и 3—5.

Следовательно, если в узле сходятся три стержня, два из которых лежат на одной прямой, то усилия в этих двух стержнях, при отсутствии в узле внешней нагрузки, равны друг другу по числовой величине и по знаку, а усилие в третьем стержне равно нулю.