Эквивалентность классов автоматов Мура и Мили

 

Каждому автомату Мили, соответствует эквивалентный ему автомат Мура.

Каждому автомату Мура, соответствует эквивалентный ему автомат Мили.

Следовательно классы автоматов Мили и Мура эквивалентны

 

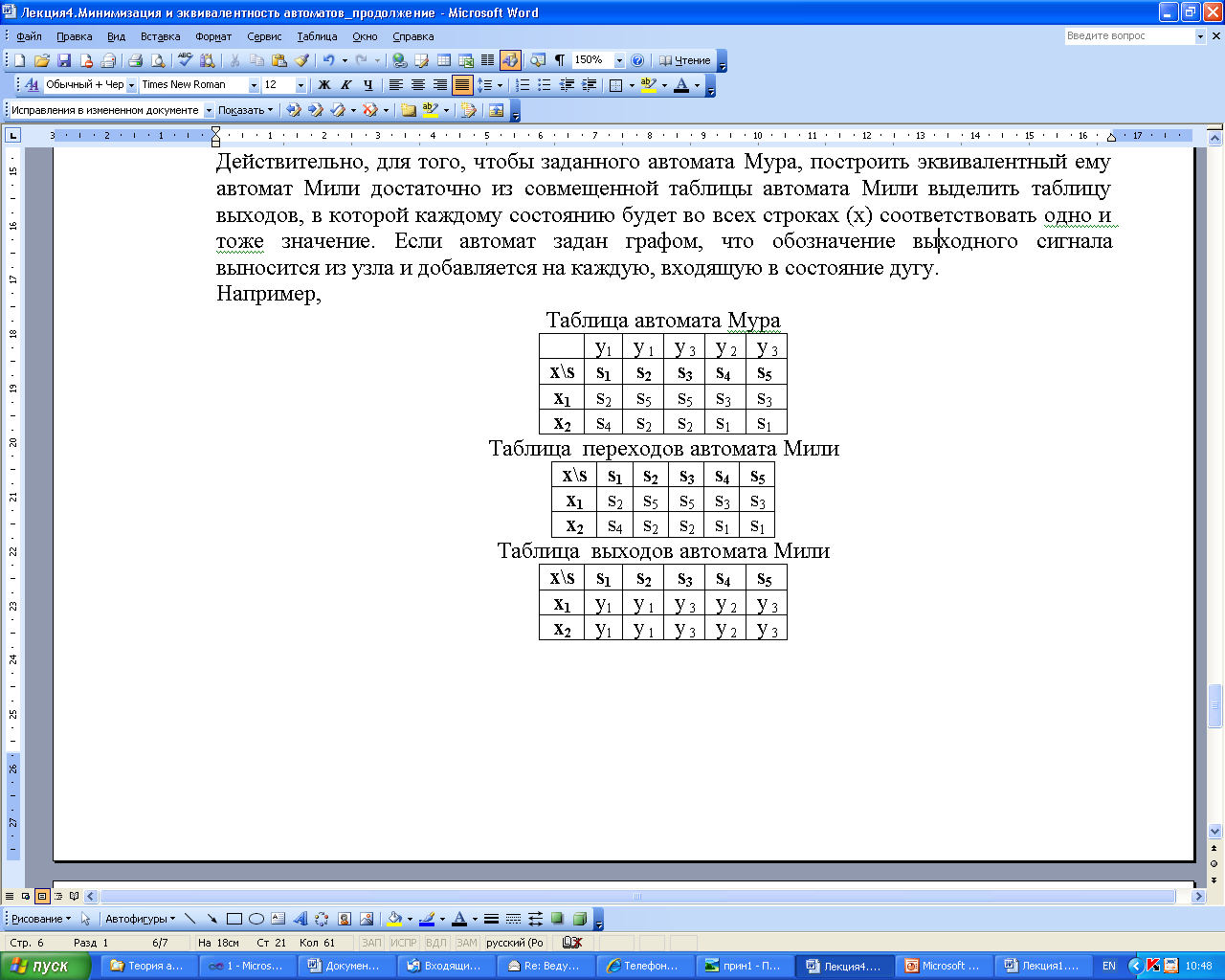Построение автомата Мили по автомату Мура.

Из совмещенной таблицы автомата Мура выделить таблицу выходов, в которой каждому состоянию будет во всех строках (x) соответствовать одно и тоже значение выходного сигнала.

 

 

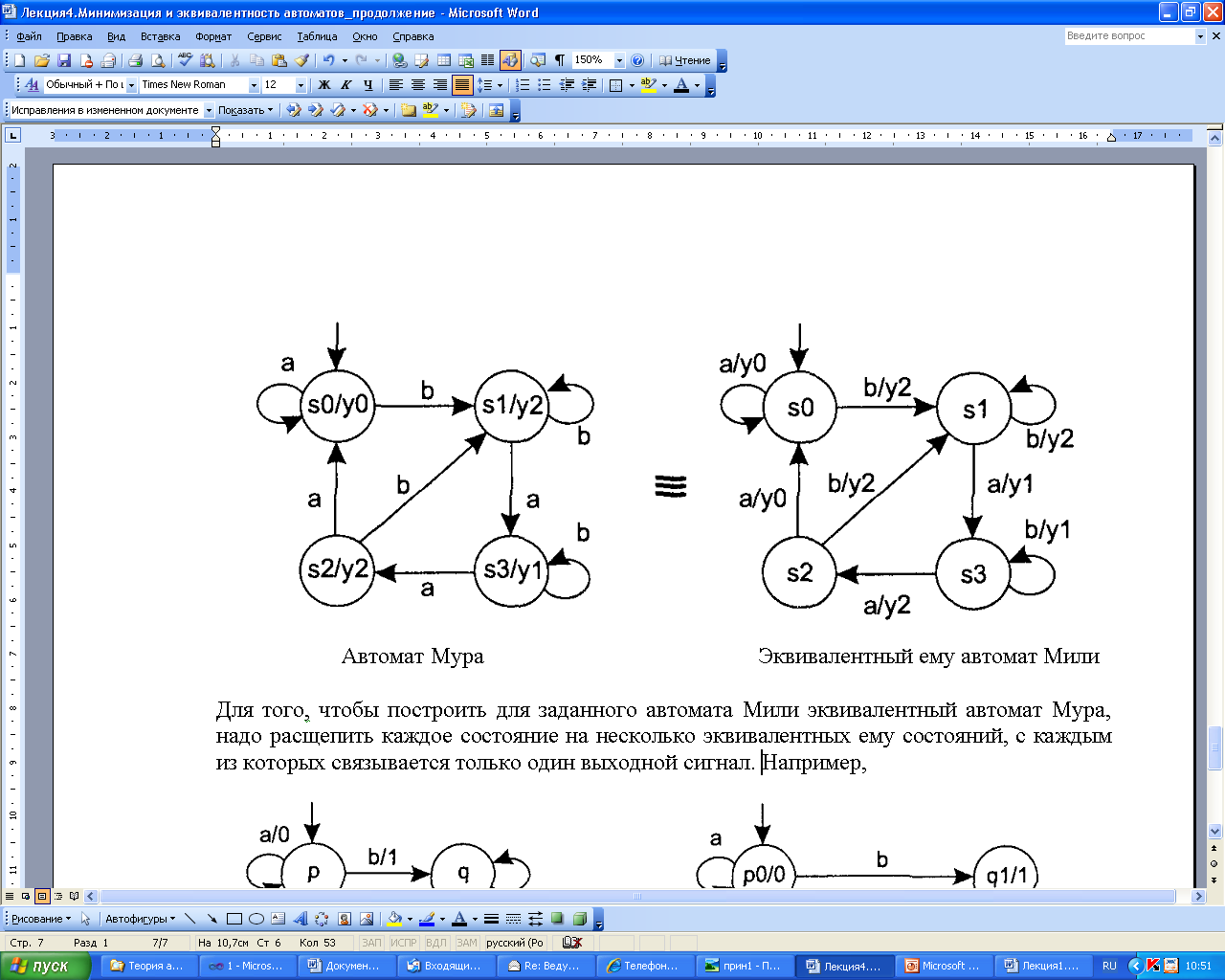
Если автомат задан графом, то обозначение выходного сигнала выносится из узла и добавляется на каждую входящую в состояние дугу.

 

 

Если автомат при входе в состоянии s может генерировать k различных выходных сигналов {y_i1,y_i2….,y_ik}, то состояние s расщепляется на k состояний {(s₁/y_i1)(s₂/y_i2),…,(s_k/y_ik)}.

Если для состояния s автомат Мили и некоторого входного сигнала xt

· δ(s, x_t)=p,

· λ(s, x_t)=y_t,

то для эквивалентного ему автомата Мура должно быть справедливо

· δ((s₁/y_i1), x_t)=(p_j1/y_t)

· δ((s₂/y_i2), x_t)= (p_j2/y_t)

· ………….

· δ((s_k/y_ik), x_t)= (p_jm/y_t)

 

 

Алфавит. Цепочки. Операции над цепочками. Понятие языка. Свойства языков. Примеры языков. Конструкторы и распознаватели языка.

Под алфавитом å будем понимать непустое конечное множество символов.

Цепочка, или строка – это последовательность символов некоторого алфавита, при этом символы в строке могут повторяться. Для цепочки важен ее состав, порядок символов и их количество.

Длиной цепочки является количество символов в ней.

Две цепочки α и β совпадают (равны): α = β, если они имеют один и тот же состав и порядок символов и их количество.

Цепочка, не содержащая символов, называется пустой цепочкой, обозначается через ε или λ.

Любая последовательно взятая часть цепочки является ее подцепочкой, собственный суффикс – это часть строки, содержащая ее последний символ и не содержащая первого, собственный префикс – это часть строки, содержащая первый символ и не содержащая последнего.

Над цепочками можно выделить следующие операции:

Конкатенацией, или сцеплением (сложением) цепочек, называется строка, полученная их объединением. Свойства: Так как в цепочке важен порядок символов, очевидно, что операция сложения не коммутативна. Конкатенация ассоциативна.

Обращение цепочки x – это запись ее символов в обратном порядке, обозначается x^R.

Итерация цепочки n раз – это ее сцепление (повторение) n раз, обозначается aⁿ.

Свойства пустой цепочки

· | ε | = 0;

· ∀ α: ε α = α ε = α;

· ε ^R = ε;

· ∀ n≥0: ε ⁿ = ε ;

· ∀ α: α ⁰ = ε.

 

Определение языка.

Если å – некоторый алфавит, то:

· å⁺ – множество всех цепочек над алфавитом å без ε.

· å* – множество всех цепочек над алфавитом å, включая ε.

Языком L над алфавитом Σ называют произвольное множество цепочек из символов этого алфавита. Такой язык принято обозначать L(Σ).

Свойства языков:

· Для любого языка L(Σ) справедливо L(Σ) Í Σ*.

· Язык L(Σ) включает в себя язык L¢(Σ): L¢(Σ) Í L(Σ), если "aÎL¢(Σ) aÎL(Σ).

· Два языка совпадают (эквивалентны): L¢(Σ) = L(Σ), если L¢(Σ) Í L(Σ) и L(Σ) Í L¢(Σ).

· Конкатенацией (объединением) языков L₁ и L₂ называют язык L, состоящий из всевозможных сцеплений цепочек языков L₁ и L₂: L = L₁·L₂ = {x·y | x Î L₁, y Î L₂}.

· Замыкание Клини, или итерация языка L, обозначается L* и определяется рекурсивно: L⁰ = { ε }, 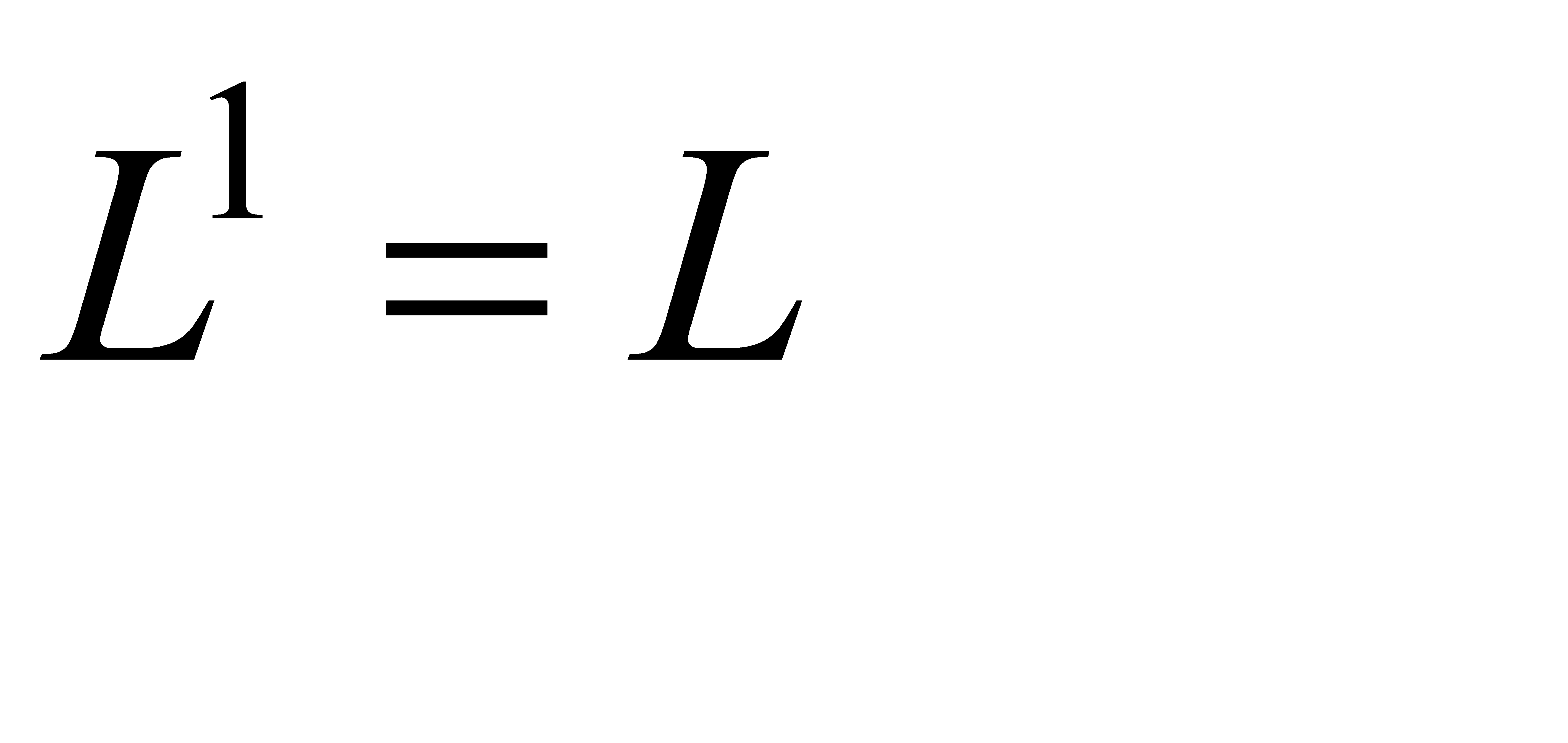; Lⁿ = L·Lⁿ-1 для n > 0, L* = È Lⁿ для всех n ³ 0.

Примеры языков:

 

Алфавит Σ = {a, b}.

· L₁= ∅ — пустой язык;

· L₂={e} - язык, содержащий только пустую цепочку (L₁ и L₂ - различные языки)

· L₃ - язык, содержащий цепочки из a и b, длина которых не превосходит 2

· L₄ - язык, включающий всевозможные цепочки из a и b, содержащие четное число a и четное число b

· L₅ - язык цепочек из a, длины которых представляют собой квадраты натуральных чисел.

 

Cпособы задания языка:

· Перечисление всех допустимых цепочек языка (нереализуем для языков, содержащих бесконечное число цепочек).

· Указание способа порождения цепочек языка– применение т.н. генератора или конструктора.

· Задание метода распознавания цепочек языка – применение распознавателя.

Конструкторы языка представляют собой набор правил, по которым можно построить все слова языка и нельзя построить слово никакого другого языка. К конструкторам относятся грамматики, синтаксические диаграммы, регулярные выражения.

Распознаватель языка– некоторое абстрактное устройство. Подавая на его вход любое слово, от распознавателя получают ответ – принадлежит ли это слово языку. К распознавателям относятся различного вида конечные автоматы.

 

 

Определение порождающей грамматики. Терминальные и нетерминальные символы, правила, целевой (начальный) символ. Понятия вывода, выводимости, сентенциальной формы грамматики. Язык, порождаемый грамматикой.

Порождающей грамматикой G называется четверка G(T,N,P,S), где

T – конечное множество терминальных (основных) символов представляет собой алфавит языка, то есть из терминальных символов и состоят цепочки языка, порождаемого грамматикой. Будем обозначать терминальные символы малыми латинскими буквами.

N – конечное множество нетерминальных символов представляет собой вспомогательный алфавит, то есть это символы, которые используются при описании языка, но не входят в алфавит языка (слова, понятия, конструкции языка). Будем обозначать нетерминальные символы заглавными латинскими буквами.

P – множество правил вывода (продукций) вида a ® b, aÎV⁺, bÎV*, где V=TÈN–полный алфавит грамматики G.

SÎN – начальный (целевой) нетерминальный символ грамматики G, с которого начинается процесс порождения цепочек языка.

Выводимость.

Выводом называется процесс порождения цепочек языка на основе правил определяющей язык грамматики.

Цепочка b=d₁gd₂ называется непосредственно выводимой из цепочки a=d₁wd₂ (aÞb)в грамматике G d₁,g,d₂ÎV^*,wÎV⁺,если в грамматике G существует правило w ® g.

Другими словами цепочка b выводима из цепочки a в том случае, если можно взять несколько символов в цепочке a, заменить их на другие символы согласно правилу грамматики и получить при этом цепочку b.

Цепочка b называется выводимой из цепочки a – обозначается a Þ* b, если выполняется одно из двух следующих условий:

§b непосредственно выводима из a: a Þ b;

§$g, такая, что: g выводима из a и b непосредственно выводима из g (a Þ* g и g Þ b).

Другими словами b выводима из цепочки a, если она либо непосредственно выводима, либо можно построить последовательность непосредственно выводимых цепочек от a к b: aÞg1Þg2Þ...Þgi Þ gi+1 Þ...g_n Þb

Вывод называется левосторонним (правосторонним), если в нем на каждом шаге вывода правило грамматики применяется к самому левому (правому) нетерминальному символу в цепочке.

Вывод называется законченным, если из полученной цепочки нельзя сделать более ни одного шага, т.е. если полученная цепочка пустая или содержит только терминальные символы грамматики.

Сентенции.

Цепочка символов aÎV^* называется сентенциальной формойграмматики G(T,N,P,S), если она выводима из целевого символа грамматики S: S Þ^* a. Если цепочка получена в результате законченного вывода, она называется сентенцией.

Например, цепочка aabb является сентенцией грамматики G1.

Язык, порождаемый грамматикой – это множество всех сентенций этой грамматики.

n Очевидно, что язык порождаемой грамматикой G1 можно описать как L(G₁)={aⁿbⁿ| n³0}.