 |
Главная |
Кусочно-определённые базисные функции
|
из
5.00
|
В рассмотренных ранее методах аппроксимации предполагалось, что базисные  , входящие в разложение
, входящие в разложение  были определены одним выражением (одной формулой) на всей области
были определены одним выражением (одной формулой) на всей области  , а интегралы в аппроксимирующих выражениях вычислялись сразу по всей области.
, а интегралы в аппроксимирующих выражениях вычислялись сразу по всей области.
Альтернативный подход состоит в разбиении области  на ряд подобластей или элементов
на ряд подобластей или элементов 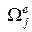 и использовании базисных функций, определённых кусочным способом (с применением различных выражений для разных подобластей
и использовании базисных функций, определённых кусочным способом (с применением различных выражений для разных подобластей 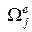 , из которых составлена вся область), и затем в построении аппроксимации
, из которых составлена вся область), и затем в построении аппроксимации 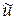 отдельно на каждой области.
отдельно на каждой области.
В этом и будет состоять основная идея метода конечных элементов.
Рассмотрим построение аппроксимации для произвольной функции  , определённо на отрезке
, определённо на отрезке  . Разобьем область
. Разобьем область  на
на  неперекрывающихся отрезков (элементов)
неперекрывающихся отрезков (элементов)  точками (узлами)
точками (узлами)
 .
.

Для приближения заданной функции  будем использовать систему функций
будем использовать систему функций 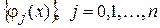 , каждая из которых представляет собой кусочно-линейную функцию
, каждая из которых представляет собой кусочно-линейную функцию
 ,
,  (1)
(1)
где  – длина отрезка.
– длина отрезка.

Эти функции называются глобальными базисными функциями и обладают тем свойством, что 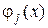 отличны от нуля только в подобласти
отличны от нуля только в подобласти  (только на элементах, примыкающих к узлу
(только на элементах, примыкающих к узлу 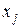 ), причем
), причем


Тогда, глобальную аппроксимацию заданной функции  можно записать в виде
можно записать в виде
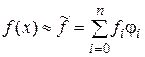 в
в  , (2)
, (2)
где  – значение функции в узле
– значение функции в узле  . Постановка соответствующих значений в узлах
. Постановка соответствующих значений в узлах  гарантирует, что это представление автоматически принимает нужные значения в граничных точках отрезка.
гарантирует, что это представление автоматически принимает нужные значения в граничных точках отрезка.
На каждом элементе  функция
функция  может быть выражена с помощью двух линейных базисных функций элемента
может быть выражена с помощью двух линейных базисных функций элемента
 и
и  . (3)
. (3)
Тогда,
 , на
, на 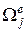 . (4)
. (4)
 На крайних сегментах
На крайних сегментах
 и
и  . (5)
. (5)
Функции (3) называют базисными или координатными функциями.
Например, для  , определенной на
, определенной на  построим кусочно-линейную аппроксимацию для системы узлов:
построим кусочно-линейную аппроксимацию для системы узлов:  ,
, 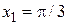 ,
,  ,
,  .
.
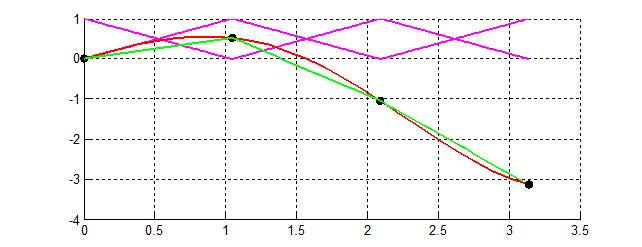
Пусть на отрезке  заданная упорядоченная система несовпадающих точек
заданная упорядоченная система несовпадающих точек 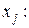 .
.  .
.
Определение. Сплайном  называется определенная на
называется определенная на  функция, принадлежащая классу
функция, принадлежащая классу 
 раз непрерывно дифференцируемых функций, такая, что на каждом промежутке
раз непрерывно дифференцируемых функций, такая, что на каждом промежутке  , – это многочлен степени
, – это многочлен степени 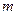 -
-  . Разность
. Разность  между степенью сплайна
между степенью сплайна 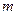 и показателем её гладкости
и показателем её гладкости  называется дефектом сплайна.
называется дефектом сплайна.
Построенная аппроксимация представляет собой сплайн первой степени дефекта один
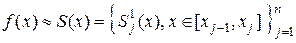 .
.
Таким образом, аппроксимация  кусочно-линейными функциями обеспечивает непрерывность и совпадение значений с аппроксимируемой функцией в узловых точках.
кусочно-линейными функциями обеспечивает непрерывность и совпадение значений с аппроксимируемой функцией в узловых точках.
Предположим, что у аппроксимируемой функции  известны не только значения в узлах, но и значения её производных. Например, требуется аппроксимировать кубическим сплайном функцию, которая, с производной, принимает в заданных точках
известны не только значения в узлах, но и значения её производных. Например, требуется аппроксимировать кубическим сплайном функцию, которая, с производной, принимает в заданных точках  отрезка
отрезка  значения
значения

| 
| ……………….. | 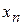
| |

| 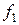
| ……………….. | 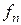
| |

| 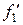
| ……………….. | 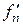
|
Эта задача может быть решена непосредственно из заданных граничных условий. Однако на практике удобнее использовать приём, заключающийся в представлении всякого кубического сплайна линейной комбинацией четырёх простых специально подобранных базисных сплайнов 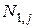 ,
,  ,
,  ,
, 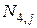 . Конкретно,
. Конкретно, 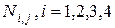 подбирают так, чтобы их краевые значения на отрезке
подбирают так, чтобы их краевые значения на отрезке  были, как указано в таблице.
были, как указано в таблице.
 Тогда искомая аппроксимация будет иметь вид
Тогда искомая аппроксимация будет иметь вид
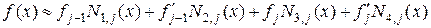 .
.
Построение самих базисных сплайнов 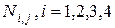 для комбинации условий, даваемых таблицей, не является сложной задачей. Например, рассмотрим построение
для комбинации условий, даваемых таблицей, не является сложной задачей. Например, рассмотрим построение 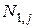 .
.
 ,
,
 .
.
Учитывая краевые условия, получим систему уравнений
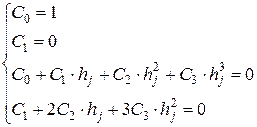 ,
,
из которой, находим
 .
.
Таким образом,
 .
.
Аналогично получаем  ,
,  ,
, 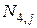 .
.

|

| |

| 
| |
|

| |

|

|
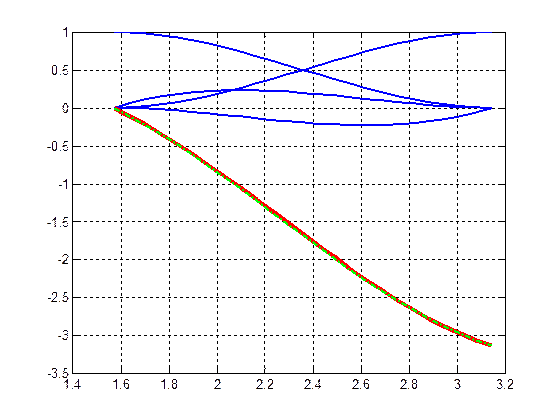
Построим аппроксимацию функции  на отрезке
на отрезке  по таблице
по таблице

| 
| 
| |

| 
| ||

| 
| 
|

|
из
5.00
|
Обсуждение в статье: Кусочно-определённые базисные функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

