Интегралы от выпуклых функций

При решении многих задач целесообразно применять следующий подход.

Разделим отрезок [a,b], на котором задана непрерывная функция f. на n частей точками 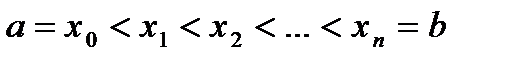. Построим прямоугольные трапеции, основаниями которых являются отрезки x_ky_k, x_k+1y_k+1, а высотами – x_kx_k+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.

Пусть функция f дважды дифференцируема на некотором промежутке и в каждой точке этого промежутка f^//(x)>0. Это означает, что функция f^/ возрастает, т.е. при движении вдоль кривой слева направо угол наклона касательной к графику возрастает. Иными словами, касательная поворачивается в направлении, обратном направлению вращения часовой стрелки. График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой. График выпуклой функции расположен «ниже» своих хорд и «выше» своих касательных. Аналогично, если f^//(x)<0, то f^/ убывает, касательная вращается по часовой стрелке и график лежит «выше» своих хорд, но «ниже» своих касательных. Такая функция называется вогнутой.

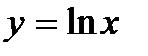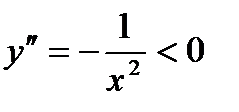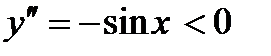Функция вогнута в области своего определения, так как . Вторая производная функции положительна на всей числовой прямой. Поэтому – выпуклая функция. Для функции вторая производная при , при , т.е. функция на интервале

вогнута, а на выпукла.

Задача 2.7. Доказать, что

Решение.

Левая часть этого неравенства равна площади прямоугольной трапеции, основания которой равны значениям функции в точках 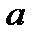и , т.е. и , а высота – 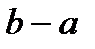. Функция выпуклая. Поэтому площадь криволинейной трапеции, ограниченной ее графиком, прямыми и отрезком [a,b] оси x, меньше площади прямоугольной трапеции. Итак,

.

Подобный результат имеет место и в общем случае. Пусть функция f на отрезке [a.b] непрерывна, положительна и выпукла. Тогда

(2.9)

Если же непрерывная, положительная функция f вогнута, то

(2.10)

2.4. Некоторые классические неравенства и их применение

Приведем вывод некоторых замечательных неравенств с помощью интегрального исчисления. Эти неравенства широко используются в математике, в том числе и при решении элементарных задач.

Пусть y=f(x) – непрерывная возрастающая при x>0 функция. Кроме того, f(0)=0, f(a)=b, где a, b некоторые положительные действительные числа. Из школьного курса математики известно, что если функция f возрастает и непрерывна на некотором промежутке, то существует функция f^-1, обратная функции f. Ее область определения совпадает с множеством значений f. функция f^-1 непрерывна и возрастает в области своего определения.

Отсюда следует, что для данной функции f существует непрерывная возрастающая обратная функция f^-1 такая, что f^-1(0)=0, f^-1(b)=a. Графики зависимостей y=f(x) и x=f^-1(y) совпадают.

Площадь S₁ криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=0, x=a, равна .

Площадь S₂ криволинейной трапеции, ограниченной линиями x=f^-1(y), x=0, y=0, y=b, равна

В последнем равенстве мы пере обозначили переменную интегрирования, что, конечно, несущественно при вычислении интеграла. Поскольку площадь прямоугольника равна сумме площадей S₁ и S₂, то

Может оказаться, что f(a) не равно заданному числу b, т.е. f(a)>b или f(a)<b.

В каждом из этих случаев площадь прямоугольника меньше суммы площадей криволинейных трапеций, равной S₁+S₂.

Объединяя эти три случая, получаем следующий результат.

Пусть f и f^-1 – две непрерывные возрастающие взаимно обратные функции, обращающиеся в нуль в начале координат. Тогда для a>0, b>0 имеет место неравенство

(2.13)

Равенство имеет место тогда и только тогда, когда b=f(a). Это неравенство называют неравенством Юнга. Оно является источником получения других важных неравенств.

Пример 2.10. Функция f, где f(x)=x, удовлетворяет условиям, при которых справедливо соотношение (1). Далее.,f^-1(x)=x. Поэтому

(2.14)