 |
Главная |
Приведение пространственной системы сил к вектору и к главному моменту
|
из
5.00
|
Приведение пространственной системы сил к главному вектору и к главному моменту. Пусть на абсолютно твердое тело действует произвольная пространственная система сил  , тогда справедлива теорема.
, тогда справедлива теорема.

Эта система сил может быть заменена одной силой  и парой сил, момент которой
и парой сил, момент которой  . Причем сила
. Причем сила  , называемая главным вектором пространственной системы сил, определяется формулой:
, называемая главным вектором пространственной системы сил, определяется формулой:  (1) и приложена в выбранном центре О. А момент
(1) и приложена в выбранном центре О. А момент  , называемый главным моментом пространственной системы сил, определяется формулой
, называемый главным моментом пространственной системы сил, определяется формулой  (2) , т. е. равен геометрической сумме моментов всех сил системы относительно выбранного центра приведения.
(2) , т. е. равен геометрической сумме моментов всех сил системы относительно выбранного центра приведения.
Доказательство этого утверждения основывается на лемме о параллельном переносе сил. В соответствии с ней все силы исходной системы перенесем параллельно себе в выбранную точку приведения О, при этом получим систему исходящих сил. Как известно, такая система может быть заменена равнодействующей  , приложенной в точке О и определяемой формулой (1). В соответствии с леммой, для того чтобы состояние тела не изменилось при выполненном переносе сил, необходимо к телу приложить n пар сил, моменты которых относительно центра О определялись соотношениями:
, приложенной в точке О и определяемой формулой (1). В соответствии с леммой, для того чтобы состояние тела не изменилось при выполненном переносе сил, необходимо к телу приложить n пар сил, моменты которых относительно центра О определялись соотношениями:  (3).По теореме о сложении пар сил эта система пар сил может быть заменена одной парой, момент которой равен геометрической сумме моментов указанных пар сил и определялся формулой (2). Главный момент Мо этой результирующей пары обычно изображают приложенным в центре О, хотя он является свободным вектором и может переноситься параллельно себе в пространстве.
(3).По теореме о сложении пар сил эта система пар сил может быть заменена одной парой, момент которой равен геометрической сумме моментов указанных пар сил и определялся формулой (2). Главный момент Мо этой результирующей пары обычно изображают приложенным в центре О, хотя он является свободным вектором и может переноситься параллельно себе в пространстве.

Сложение параллельных сил в пространстве.
Рассмотрим систему параллельных сил  прилаженных в точках
прилаженных в точках  и направленных в одну сторону. Найдем точку С2 через которую проходит равнодействующая
и направленных в одну сторону. Найдем точку С2 через которую проходит равнодействующая 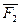 двух сил
двух сил 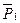 , и
, и  , потом точку С3, через которую проходит равнодействующая
, потом точку С3, через которую проходит равнодействующая  , сил
, сил 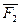 , и
, и 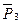 и т.д.
и т.д.
 - центр параллельных сил.
- центр параллельных сил.
Численная величина равнодействующей равна, очевидно, сумме величины заданных сил:  .Проектируя обе части равенства на оси координат, получим выражение для координат х0, у0, z0 центра параллельных сил:
.Проектируя обе части равенства на оси координат, получим выражение для координат х0, у0, z0 центра параллельных сил:

где хi уi, zi - координаты приложения силы  .
.
Когда дана система параллельных сил, направленных в разные стороны, то можем разделить силы этой системы на две группы, каждая из которых включает силы, направленные в одну сторону. Находя равнодействующую, приведем данную систему к системе двух антипараллельных сил.
Центр тяжести тела.
Равнодействующая всех сил тяжести, действующих на частицы тела, будет численно, равна весу тела, а ее линия действия будет проходить ,через точку, совпадающую с центром параллельных сил тяжести частиц тела. При изменении тела в пространстве, что соответствует изменению направлений сил относительно тела, эта точка согласно свойству центра параллельных сил не изменяет своего положения по отношению к телу. Точка, являющаяся центром параллельных сил тяжести частиц тела, называется центром тяжести данного тела.
Пусть имеем некоторое тело. Разобьем его на отдельные частицы и обозначим через Побьем всего тела, DV- объем какой-нибудь частицы, а через DP- вес этой частицы, r- плотность тела. Тогда радиус-вектор или координаты центра масс тела определяются:
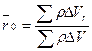 ;
;
 ;
;
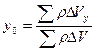 ;
;
 .
.
Иногда приходится находить центр тяжести пластинок. Толщина пластинки по сравнению с двумя другими ее измерениями очень мала и всюду одинакова, поэтому можем находить центр тяжести не объема, а площади. Тогда радиус-вектор и координаты центра тяжести пластинки, расположенной в плоскости:
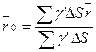 ;
;
будут определяться формулами:
 ;
;  ,
,
где  .
.
В некоторых случаях требуется найти центр тяжести материальной линии, т. е. тела, у которого площадь поперечного сечения всюду одинакова и очень мала по сравнению с длиной. Тогда определение центра тяжести тела сведется к определению центра тяжести линии, положение которой найдется по формуле:  .
.
Теорема 1. Площадь поверхности, полученной вращением дуги плоской кривой вокруг оси, лежащей в ее плоскости, но не пересекающей, равна длине этой дуги, умноженной на длину окружности, описанной ее центром тяжести.
Теорема 2. Объем тела вращения, образованного вращением плоской фигуры вокруг оси, лежащей в плоскости этой фигуры и ее не пересекающей, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести площади фигуры.
Метод группировки.
В задачах о нахождении центра тяжести тела иногда бывает легче определить центры тяжести отдельных его частей, на которые можно разбить тело. Пусть данное тело разбили на несколько частей и определили центр тяжести каждой такой части тела, т. е. нашли:  и т.д.
и т.д.
Если теперь сгруппировать слагаемые, то получим: 
|
из
5.00
|
Обсуждение в статье: Приведение пространственной системы сил к вектору и к главному моменту |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

