Алгоритм решения квадратных уравнений

+bx+c=0

1.Найти дискриминант D по формуле D= 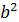-4ac.

2.Если D<0, то квадратное уравнение не имеет корней.

3.Если D=0, то уравнение имеет один корень:

 

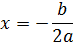
4.Если D>0, то уравнение имеет два корня:

, .

 

 

Теперь приступим к решению нашего уравнения 3 -10х+3=0,

где =3, b=-10 а с=3.

Находим дискриминант:

 

D= -4*3*3=64

Поскольку D>0, то у данного уравнения два корня. Находим их:

; .

 

Таким образом, корнями многочлена f(x)=3 -10+3 будут являться числа 3 и .

 

Схема Горнера

 

Схема Горнера(или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы полиномов (одночленов), при заданном значении переменной.Она, в свою очередь, и помогает нам выяснить, является ли число корнем данного многочлена или нет.

Для начала рассмотрим как делится многочлен f(x )на двучлен g(x).

Это можно записать следующим образом: f(x):g(x)=n(x), где f(x)- делимое, g(x)- делитель а n(x)- частное.

Но в случае, когда f(x) не делится нацело на g(x) имеет место общая запись выражения

 

.

При это степень r(x)< deg s(x), в таком случае можно сказать, что делится на 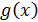с остатком .

Рассмотрим деление многочлена на двучлен. Пусть

 

,

+...+ .

 

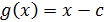
Получаем

 

 

Где r- число т.к. степень r должна быть меньше степени (x-c).

Умножим s(x) на 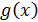и получим

 

 

Отсюда

 

Таким образом, при делении на двучлен можно определять коэффициенты частного по полученным формулам. Подобный способ определения коэффициентов и называется схемой Горнера.

 

				...
	+			...
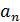
c				...	r

 

Теперь рассмотрим несколько примеров применения схемы Горнера.

 

Пример. Выполнить деление многочлена f(x)= на x+3.

Решение.В начале необходимо записать (x+3) в виде (x-(-3)), поскольку в самой схеме будет участвовать именно -3.В верхней строке мы будем записывать коэффициенты, в нижней- результат действий.

 

 

 

				-5	-35
	+	1*(-3)=-3		-12
-3		3+(-3)=0		-17

 

 

По полученным результатам запишем

 

 

Таким образом, мы получили f(x)= 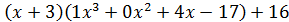с остатком r(x)= 16.

 

Пример. Выполнить деление многочлена f(x)= на x-2.

Решение.

 

			-3	-2
	+

 

f(x)=(x-2)(1 )+16.

 

Нахождение корней по схеме Горнера. Виды корней

По схеме Горнера можно находить целочисленные корни многочлена f(x). Рассмотрим это на примере.

Пример. Найти все целочисленные корни многочлена f(x)= , при помощи схемы Горнера.

Решение.Коэффициенты данного многочлена- целые числа. Коэффициент перед старшей степенью(в нашем случае перед 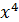) равен одному. Поэтому, целочисленные корни многочлена мы будем искать среди делителей свободного члена (у нас это 15), это числа:

Начнем проверку с числа 1.

 

Таблица №1

			-21	-20
	+			-18	-38
			-18	-38

 

 

Из полученной таблицы видно, что при =1 многочлен многочлена f(x)= , мы получили остаток r=192, а не 0, из этого следует, что единица не является корнем. Поэтому продолжим проверку при =-1. Для этого мы не будем создавать новую таблицу, а продолжим в старой, а уже не нужные данные зачеркнем.

 

Таблица №2

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22

 

 

Как мы видим из таблицы, в последней ячейке получился нуль, а это значит, что r=0. Следовательно? число -1 является корнем данного многочлена. Поделив наш многочлен многочлена f(x)= на ( )=x+1 мы получили многочлен

 

f(x)=(x+1)( ),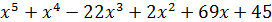

 

коэффициенты для которого мы взяли из третей стоки таблицы № 2.

 

Также мы можем сделать равносильную запись

 

(x+1)( ). Пометим его (1)

 

Теперь необходимо продолжить поиск целочисленных корней, но только сейчас мы уже будем искать корни многочлена 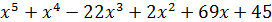. Искать эти корни мы будем среди свободного члена многочлена, числа 45.

Еще раз проверим число -1.

 

Таблица №3

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22

 

Таким образом, число -1 является корнем многочлена , его можно записать в виде

 

(2)

 

 

С учетом равенства (2) мы можем записать равенство (1) в следующем виде

(3)

=

 

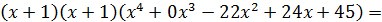
Теперь ищем корни для многочлена 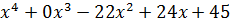, опять же среди делителей свободного члена. Вновь проверим число -1.

 

Таблица №4

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21

 

 

По таблице мы видим, что число -1 является корнем многочлена .

 

(3*)

С учетом (3*) мы можем переписать равенство (2*) как:

 

(5)

 

Теперь будем искать корень для . Вновь смотрим делители свободного члена. Начнем проверку вновь с числа -1.

 

Таблица №5

 

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21
	+	-1
-1		-2	-19

 

 

У нас получился остаток не равный нулю, а это значит, что число -1 не является корнем для многочлена . Проверим следующее число 1.

Таблица №6

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21
	+	-1
-1		-2	-19
	+			-21
			-21

 

 

И мы видим, что опять не подходит, остаток r(x)= 24.Берем новое число.

Проверим число 3.

 

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21
	+	-1
-1		-2	-19
	+			-21
			-21
	+			-45
			-15

 

Таблица №7

 

 

r(x)= 0, это значит, что число 3 является корнем многочлена , этот многочлен мы можем записать как:

 

=(x-3)( )

 

Учитывая получившееся выражение, мы можем записать равенство (5) в следующем виде:

 

( x-3)( ) (6)

 

Проверим теперь для многочлена

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21
	+	-1
-1		-2	-19
	+			-21
			-21
	+			-45
			-15
	+

Таблица №8

 

Исходя из таблицы, мы видим, что число 3 это корень многочлена . Теперь запишем следующее:

 

 

Запишем равенство (5*), с учетом получившегося выражения, следующим образом:

 

( x-3)( )= = .

 

Найдем корень для двучлена 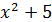среди делителей свободного члена.

Возьмем число 5

 

Таблица №9

			-21	-20
	+			-18	-38
			-18	-38
	+	-1	-1		-2	-69	-45
-1			-22
	+	-1			-24	-45
-1			-22
	+	-1			-45
-1		-1	-21
	+	-1
-1		-2	-19
	+			-21
			-21
	+			-45
			-15
	+
	+	-5
-5

 

r(x)=0, следовательно, 5 является корнем двучлена .

 

Таким образом, мы можем записать

 

.

 

Решением данного примера будет являться таблица№8.

Как видно из таблицы, числа -1;3;5 – корни многочлена.

 

Теперь перейдем непосредственно к видам корней.

 

-1- корень третьей степени, поскольку скобка (x+1) находится в третьей степени;

3- корень второй степени, скобка(x-3) во второй степени;

5- корень первой степени или, другими словами, простой.