 |
Главная |
Полиномиальная интерполяция
|
из
5.00
|
Интерполирование функций
Постановка задачи
В некоторой ограниченной области значений  на плоскости (x,y) заданы n+1 точка: {x0, y0; x1,y1; … xn,yn}, (где xi расположены в порядке возрастания) отражающие в дискретном виде функциональную зависимость y от x. Эти точки называются узлами интерполяции. Решить задачу интерполирования, это значит найти значение y(x) для промежуточных значений x. Задача интерполирования решается путем построения интерполяционной функции F(x), такой, что
на плоскости (x,y) заданы n+1 точка: {x0, y0; x1,y1; … xn,yn}, (где xi расположены в порядке возрастания) отражающие в дискретном виде функциональную зависимость y от x. Эти точки называются узлами интерполяции. Решить задачу интерполирования, это значит найти значение y(x) для промежуточных значений x. Задача интерполирования решается путем построения интерполяционной функции F(x), такой, что 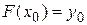 ,
, 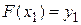 , … ,
, … , 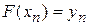 . Иначе говоря – проходящей через все узлы интерполяции. После этого искомое значение y(x) вычисляется как значение F(x).
. Иначе говоря – проходящей через все узлы интерполяции. После этого искомое значение y(x) вычисляется как значение F(x).
Если приближенное значение зависимости ищется за пределами области, т.е. при 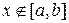 , то это называют экстраполирование.
, то это называют экстраполирование.
Полиномиальная интерполяция
Если в качестве интерполяционной функции строится алгебраический многочлен – полином, то говорят о полиномиальной интерполяции. Согласно теореме единственности, через 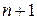 точку можно провести только один полином n-ой степени. Этот полином может иметь различную форму записи. Различают записи с помощью формул Ньютона и Лагранжа.
точку можно провести только один полином n-ой степени. Этот полином может иметь различную форму записи. Различают записи с помощью формул Ньютона и Лагранжа.
Полином Лагранжа. Наиболее общим вариантом интерполяционного полинома является полином Ланранжа. Он может быть получен при переменном шаге по x между узлами интерполяции. Не допускается лишь совпадение x-координат узлов.
Для построения интерполяционного полинома Лагранжа используется базис, составленный из полиномов n-ой степени: 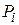 (x) (i=0,n), удовлетворяющих условиям:
(x) (i=0,n), удовлетворяющих условиям: 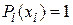 ;
; 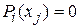 при
при 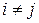 . Pi(x) имеет следующий вид:
. Pi(x) имеет следующий вид:
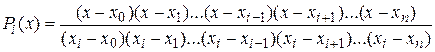 .
.
Интерполяционный полином Лагранжа 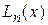 строится в виде:
строится в виде:
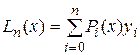 ,
,
Нетрудно показать, что он проходит через все узлы интерполяции: 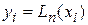 .
.
Полином можно записать в общем виде:
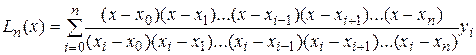 .
.
Иногда его записывают как
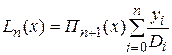 , где
, где 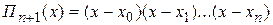 ,
,
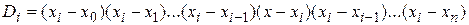 .
.
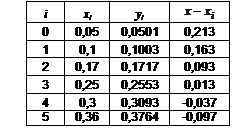
В следующем примере приведены вычисления с помощью формулы Лагранжа (неравноотстоящие узлы) функции в точке 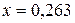 . .
| 
|
 Произведение последнего столбца таблицы дает
Произведение последнего столбца таблицы дает 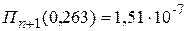 . Вычисление
. Вычисление  приведено ниже.
приведено ниже.
Окончательно 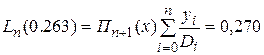 .
.
В случае равноотстоящих узлов интерполяционную формулу Лагранжа можно преобразовать к следующей форме:
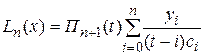 ,
,
где 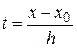 ,
,  ,
, 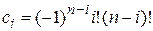 .
.
Интерполяционные полиномы Ньютона. Полиномиальная интерполяция по Ньютону производится при равноотстоящих по x узлах интерполяции. Первая интерполяционная формула Ньютона строится в виде:
 ,
,
где коэффициенты 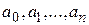 определяются из соотношения
определяются из соотношения 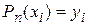 , (
, ( 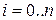 ).
).
При нахождении коэффициентов используется понятие конечной разности. Для функции 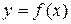 :
:
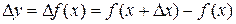 - первая конечная разность,
- первая конечная разность,
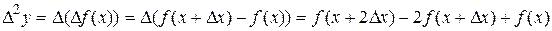 - вторая конечная разность. В узловых точках имеем:
- вторая конечная разность. В узловых точках имеем:
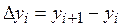 ,
, 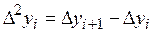 .
.
Аналогично для конечных разностей высших порядков 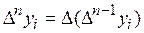 .
.
Итоговая формула, которая называется первой интерполяционной формулой Ньютона (в случае равноотстоящих узлов) имеет вид:
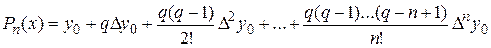 ,
,
где 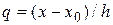 , h - шаг (расстояние между соседними точками). При малых q членами высоких порядков в формуле можно пренебречь, поэтому первую формулу Ньютон обычно используют в случае, когда x близка к х0.
, h - шаг (расстояние между соседними точками). При малых q членами высоких порядков в формуле можно пренебречь, поэтому первую формулу Ньютон обычно используют в случае, когда x близка к х0.
Ниже в таблице приведен пример таблично заданной функции и ее конечных разностей (до третьего порядка). Используя данную таблицу и формулу Ньютона (ограничиваясь членами третьего порядка по q) можно вычислить функцию, например, в точке 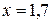 .
.
| i | xi | yi | Dyi | D2yi | D3yi |
| 1,5 | 3,247495 | 1,6618 | 0,27737 | 0,0761 | |
| 4,909297 | 1,93917 | 0,35347 | 0,11198 | ||
| 2,5 | 6,848472 | 2,29265 | 0,46545 | 0,12044 | |
| 9,14112 | 2,7581 | 0,58588 | 0,09941 | ||
| 3,5 | 11,89922 | 3,34398 | 0,68529 | 0,05404 | |
| 15,2432 | 4,02927 | 0,73933 | -0,0046 | ||
| 4,5 | 19,27247 | 4,76861 | 0,73478 | -0,062 | |
| 24,04108 | 5,50338 | 0,67274 | |||
| 5,5 | 29,54446 | 6,17612 | |||
| 35,72058 |
Тогда 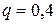 ,
, 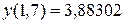 .
.
Примечание. При вычислениях, в качестве х0 лучше выбирать ближайшую точку к х. Например, для точки 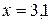 удобней выбрать
удобней выбрать
 , тогда соответственно
, тогда соответственно 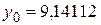 ,
, 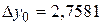 …
…
При вычислениях значений функции, близких к концу таблицы, первая формула Ньютона может оказаться мало пригодной из-за того, что члены высоких порядков велики и их нельзя сократить. В этом случае используют вторую формулу Ньютона, которая получается, если полином искать в виде:

Вторая интерполяционная формула Ньютона имеет вид:
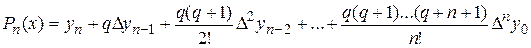 ,
,
где 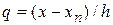 .
.
Вычислим функцию в точке 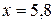 , тогда
, тогда 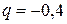 ,
, 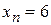 ,
, 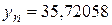 ,
, 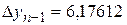 ,
,  …
…
и, в результате (с точностью до третьего порядка по q) 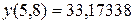 .
.
|
из
5.00
|
Обсуждение в статье: Полиномиальная интерполяция |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

