 |
Главная |
Лабораторная работа №17. Найти приближенное решение задачи Дирихле для уравнения Лапласа в квадратной области
|
из
5.00
|
Найти приближенное решение задачи Дирихле для уравнения Лапласа в квадратной области (квадрат АВСD) при 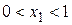 ,
, 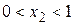 . Шаг сетки
. Шаг сетки 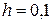 , погрешность
, погрешность 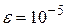 . Исследовать влияние параметра
. Исследовать влияние параметра 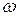 из интервала
из интервала  с шагом 0,1 на сходимость итерационного процесса. Найти оптимальное значение
с шагом 0,1 на сходимость итерационного процесса. Найти оптимальное значение 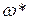 . Ниже в таблице приведены функции, задающие искомую функцию на сторонах квадрата.
. Ниже в таблице приведены функции, задающие искомую функцию на сторонах квадрата.
| N | AB | BC | CD | FD |
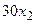
| 
| |||

| 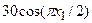
| 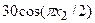
| 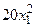
| |
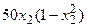
| 
| |||

| 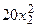
| 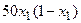
| ||
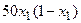
| 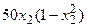
| 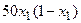
| ||

| 
| 
| 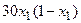
| |

| 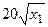
| 
| 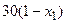
| |

| 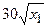
| 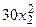
| 
| |
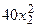
| 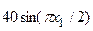
| |||
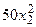
| 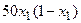
| 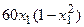
| ||
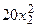
| 
| 
| ||
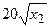
| 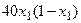
| 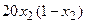
| ||

| 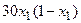
| 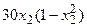
| 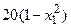
| |
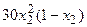
| 
| 
| ||

| 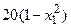
| 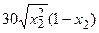
| ||
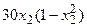
| 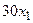
| |||

| 
| 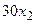
| 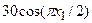
| |

| 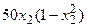
| |||
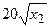
| 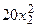
| 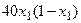
| ||

| 
| 
| ||
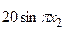
| 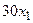
| 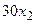
| 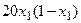
| |
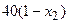
| 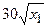
| 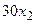
| 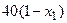
| |
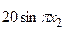
| 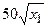
| 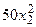
| 
| |
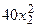
| 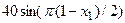
| |||
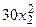
| 
| 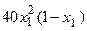
| ||

| 
| 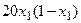
| ||
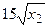
| 
| 
| ||

| 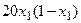
| 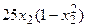
| 
| |
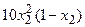
| 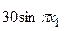
| 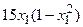
| ||

| 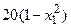
| 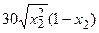
|
Уравнение колебаний.Рассматривается задача определенная на отрезке 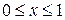 по пространственной координате, и на
по пространственной координате, и на 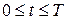 по временной. В этой области находится функция
по временной. В этой области находится функция 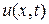 , удовлетворяющая уравнению:
, удовлетворяющая уравнению:
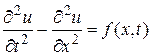 ,
, 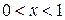 ,
, 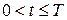 ,
,
начальными условиями:  ,
, 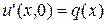 при
при 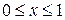
и граничными условиями:  ,
,  при
при 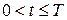 .
.
Здесь  ,
, 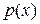 ,
,  ,
,  ,
,  - заданные функции.
- заданные функции.
После введения сетки { 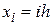 ,
, 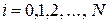 ,
, 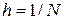 ;
; 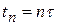 ,
,  ,
, 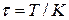 } и перехода к конечным разностям получаем систему разностных уравнений:
} и перехода к конечным разностям получаем систему разностных уравнений:
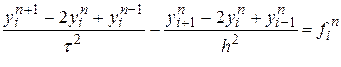 ,
, 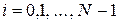 ,
,  .
.
Решение на 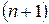 -ом шаге по времени выражается явным образом. Погрешность аппроксимации этой схемы
-ом шаге по времени выражается явным образом. Погрешность аппроксимации этой схемы  . Она устойчива при
. Она устойчива при  .
.
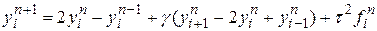 , где
, где 
Граничные условия переписываются:
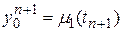 ,
,  при
при  .
.
Для решения уравнения необходимо знать два первых временных слоя, которые выражаются из начальных условий.
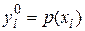 ,
, 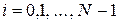 , для нахождения
, для нахождения  используется аппроксимация производной:
используется аппроксимация производной: 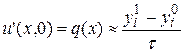 , откуда
, откуда  .
.
Если аппроксимировать производную со вторым по t порядком точности, то получается формула: 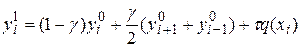 .
.
Лабораторная работа №18
Найти приближенное решение уравнения колебаний при заданных начальных и краевых условиях 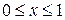 ,
, 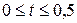 ,
, 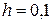 ,
, 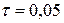 ,
,  .
.
| N | 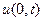
| 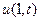
| 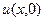
| 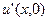
|

| 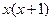
| 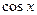
| ||
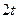
| -1 | 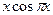
| 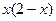
| |
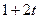
| 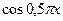
| 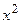
| ||
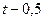
| 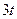
| 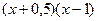
| 
| |
| 0,3 | 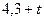
| 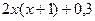
| 
| |
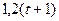
| 
| 
| ||
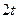
| 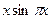
| 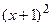
| ||
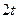
| 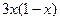
| 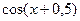
| ||
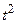
| 1,5 | 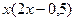
| 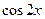
| |
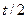
| 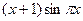
| 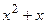
| ||
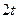
| 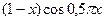
| 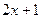
| ||

| 
| 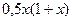
| ||
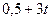
| 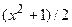
| 
| ||

| 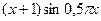
| 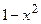
| ||

| 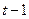
| 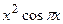
| 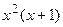
| |

| 
| 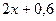
| ||
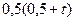
| 2,25 | 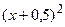
| 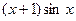
| |
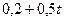
| 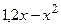
| 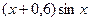
| ||
| 0,5 | 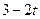
| 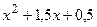
| 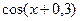
| |
| 0,5 | 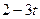
| 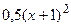
| 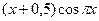
| |

| 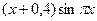
| 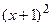
| ||

| 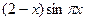
| 
| ||
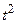
| 
| 
| ||
| 0,4 | 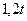
| 
| 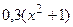
| |

| 
| 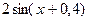
| ||

| 0,9 | 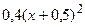
| 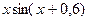
| |
| 0,5 | 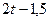
| 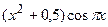
| 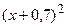
| |
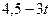
| 
| 
| ||

| 
| 
| ||
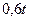
| 1,2 | 
| 
|
Физическая задача №6
Постановка задачи. Требуется найти характер установления стационарного решения задачи №2, решая уравнение теплопроводности:
r×с×¶Т ¤¶t = l׶2T ¤ ¶t2 + Q(T). (1)
В этом уравнении r - плотность металлического проводника (2.71 кг/дм 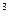 ). Остальные параметры выбрать таким же, как в предыдущей краевой задаче. Граничные условия также соответствуют краевой задаче.
). Остальные параметры выбрать таким же, как в предыдущей краевой задаче. Граничные условия также соответствуют краевой задаче.
В задании следует использовать классическую явную схему с двумя шагами по времени t = t0 = h2/(2c) и t = t0 ¤3 [2].
Требования к защите.
1. Представить зависимость от времени максимума температуры по x до момента получения стационарного решения задачи с погрешностью не более 1% по максимальному значению температуры.
2. Добиться подбором N (h =L/N), чтобы максимум температуры в момент времени t1 = 0.05L2/c был вычислен с погрешностью не более 1% (для оценки погрешности использовать прием Рунге).
3. Показать, что счет с t = t0 ¤3 обеспечивает большую точность.
Физическая задача №7
Постановка задачи полностью эквивалентна предыдущему заданию. Но в этом задании необходимо использовать неявную схему [2] и получить аналогичные результаты. Кроме того, требуется показать, что возможность использования более крупного шага по времени в неявной схеме может сократить время счета до получения стационара.
Требования к защите.
Первые два пункта аналогичны предыдущему заданию. В третьем пункте показать результаты (по интегральным характеристикам) при шагах t = t0, t = 2t0.
Физическая задача №8
Поперечные колебания струны описываются уравнением
¶2v¤¶t2 = c2׶2v¤¶x2, 0 < x < L . (1)
В этом уравнении с – скорость распространения колебаний
c = 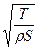 . (2)
. (2)
Здесь Т – натяжение струны (в ньютонах), r - плотность, а S – сечение струны. Самая низкая частота колебаний струны равна
F1 = c/(2L). (3)
Расчеты можно выполнять по явной схеме с порядком аппроксимации О(t2 +h2). Фиксированными параметрами считать
L=1 м, 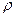 =7.8 кг/дм
=7.8 кг/дм 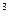 , S=4 мм
, S=4 мм  . (4)
. (4)
Величина натяжения определяет вариант задания Т=2j н (j- номер студента в группе).
Задание.
1. Вычислить самую низкую частоту F1.
2. Выполнив расчеты, показать графически характер колебаний на одном периоде при однородных граничных условиях и начальных условиях
v(0,x) = sin(p×x/L), ¶v(0,x)/¶t = 0. (4)
3. Показать графически решение (положение струны при t=2t 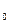 ) при нулевых начальных условиях, закрепленном левом конце (v(t,0) = 0) и заданном движении правого конца
) при нулевых начальных условиях, закрепленном левом конце (v(t,0) = 0) и заданном движении правого конца
sin(8p×F1×t) , 0 < t < t0 =1/(8 F1)
v(t,L) =
0, t > t0
4. По значению максимального значения решения в момент времени 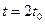 показать точность расчетов посредством перебора шага
показать точность расчетов посредством перебора шага  .
.
Физическая задача №9
Типичными уравнениями эллиптического типа являются уравнения Лапласа и Пуассона. В декартовых координатах уравнение Лапласа это равная нулю сумма вторых частных производных по трем координатам. Уравнение Пуассона отличается от уравнения Лапласа наличием в уравнении заданной функции координат 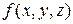 . Впервые оператор Лапласа (сумма вторых частных производных) появился в работах Эйлера. Заслуга Лапласа состояла в том, что он показал, что потенциал поля тяготения
. Впервые оператор Лапласа (сумма вторых частных производных) появился в работах Эйлера. Заслуга Лапласа состояла в том, что он показал, что потенциал поля тяготения  вне масс удовлетворяет именно уравнению Лапласа. Математический смысл уравнения Лапласа – усреднение. Зная потенциал, можно вычислить компоненты сил по уравнению
вне масс удовлетворяет именно уравнению Лапласа. Математический смысл уравнения Лапласа – усреднение. Зная потенциал, можно вычислить компоненты сил по уравнению 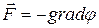 . Отметим, что Лаплас пытался выяснить - каким образом передается взаимодействие тел разделенных промежутком. Ответ на этот вопрос не получен до сих пор, но математически задача решена очень изящно. Потенциал в месте нахождения масс определяется уравнением Пуассона с заданием плотности
. Отметим, что Лаплас пытался выяснить - каким образом передается взаимодействие тел разделенных промежутком. Ответ на этот вопрос не получен до сих пор, но математически задача решена очень изящно. Потенциал в месте нахождения масс определяется уравнением Пуассона с заданием плотности  . В определенных единицах это уравнение Пуассона может быть записано в виде
. В определенных единицах это уравнение Пуассона может быть записано в виде
 .
.
Таким образом, уравнение Лапласа и Пуассона могут описывать распределение потенциала гравитационного поля, электрического и магнитного полей. Кроме того, эти уравнения описывают стационарное распределение температуры.
Задание. Итерационным методом ПВР[2] (последовательная верхняя релаксация) решить конечно-разностные уравнения, соответствующие уравнению Пуассона в области единичного квадрата с однородными граничными условиями
Du +f(x,y) = 0, u½Г =0 . (1)
f(x,y) = (i+1)×(k+1)×x×(1-x)×y×(1-y) . (2)
Целые числа i,k в формуле (2) соответствуют номеру студента в списке (N = ik). Рекомендация – число узлов по каждой координате брать не более 40. Можно считать, что искомая функция – температура, а функция  пропорциональна внутренним источникам тепла.
пропорциональна внутренним источникам тепла.
Требования к защите.
1. Дать физическую интерпретацию постановке задачи.
2. Представить изолинии полученного решения (не менее трех изолиний).
3. Показать зависимость числа итераций, необходимых для того, чтобы максимальная невязка была менее 10-5, от параметра верхней релаксации w. Для выполнения этого пункта представить число итераций для трех значений параметра релаксации (одно из них равно оптимальному значению w* = 2/(1+sin(p×h)).
4. Для максимального значения решения Um = max½u(x,y)½ получить уточненное значение по правилу Рунге-Ромберга, используя решение на трех сетках.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа №17. Найти приближенное решение задачи Дирихле для уравнения Лапласа в квадратной области |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

