Концентрация электронов в зоне и на уровнях

СТАТИСТИКА ЭЛЕКТРОНОВ

В ПОЛУПРОВОДНИКАХ

 

Для расчета концентрации электронов в кристалле надо учитывать их квантово-механическую природу и то, что в одном состоянии может находиться только два электрона.

Фазовое пространство импульсов 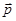или волновых векторов (энергий) электронов квантовано. Объем одной ячейки в 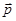-пространстве равен h³. Число электронов, приходящихся на интервал Е, Е + dE, содержащий dZ квантовых ячеек или состояний будет:

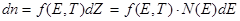, (8.1)

где – плотность квантовых состояний – число состояний, приходящихся на единичный интервал энергий.

Тогда в интервале 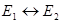число электронов:

(8.2)

 

Концентрация электронов в зоне и на уровнях

В условиях термодинамического равновесия для частиц с полуцелым спином выполняется распределение Ферми-Дирака.

, (8.3)

где E_F – электрохимический потенциал или энергия Ферми, т.е. работа, которую необходимо затратить для изменения числа частиц в системе на единицу (V = Const, T = Const).

Для E_F величина f = 1/2 при любых условиях (рис. 8.1), т.е. E_F – энергия электрона, вероятность иметь которую равна 1/2.

Рис. 8.1. Функция распределения электронов при разных температурах

При E – E_F >> kT 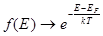(Распределение Больцмана).

Это невырожденный (идеальный) газ, а полупроводник невырожден.

 

Плотность состояний N(E)

Найдем плотность состояний в полупроводнике со сферической зоной с минимумом в центре зоны Бриллюэна (рис. 8.2). Энергия электронов у дна зоны проводимости (в p-пространстве):

(8.4)

В шаровом слое, соответствующем интервалу Е и E + dE число состояний определяется его объемом dV и размером элементарной ячейки h³; в каждом состоянии могут находиться 2 электрона:

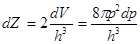(8.5)

Рис. 8.2. Изоэнергетические поверхности в р-пространстве

 

Так как из (8.4) ,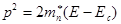

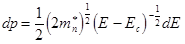, (8.6)

то

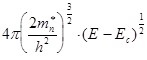(8.7)

Наибольшая плотность состояний находится у дна Е_с (рис. 8.3).

Для дырок

(8.8)

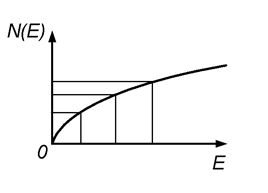
Рис. 8.3. Зависимость плотности состояний электронов от их энергии

 

При эллипсоидальной форме зоны с минимумом в стороне от центра зоны Бриллюэна (М эквивалентных минимумов) плотность состояний N(E) увеличится в M раз. Учтем сложную форму поверхности энергии.

Эллипсоид:

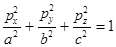
Полуоси:

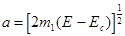
Эффективная масса плотности состояний 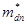позволяет пользоваться формулой для N(E) такого же вида, как и для сферической формы энергии.

Объем эллипсоида

(8.9)

(8.10)

Для учета всех минимумов:

(8.11)

Например, Si имеет 6 минимумов, m₁ = m₂

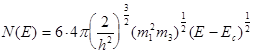
Так как m₁ = 0,19m_o, m₃ = 0,92m_o, то эффективная масса плотности состояний

Для дырок (легких и тяжелых):

Итак, концентрация электронов в зоне проводимости:

(8.12)

Концентрация электронов и дырок в зонах

Так как и вдали от дна зоны N(E) мало, то при интегрировании от дна до потолка зоны проводимости верхний предел интегрирования можно брать равным ¥. Если вести отсчет энергии от дна зоны проводимости, то нижний предел можно считать нулевым.

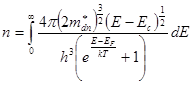(8.13)

Введем безразмерные величины:

; ,

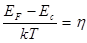где e – приведенная энергия электрона;

h – приведенный уровень Ферми, т.е. на сколько kT он отстоит от дна зоны проводимости.

Тогда:

, (8.14)

где – эффективная плотность состояний в зоне проводимости (максимальная плотность состояний).

(8.15)

Это формула для расчета плотности состояний для любого полупроводника с известной массой плотности состояний и при известной температуре Т.

Интеграл Ферми с индексом 1/2:

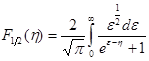(8.16)

Приближенные выражения интеграла Ферми в зависимости от величины h:

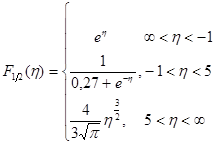(8.17)

Рассмотрим все три случая.

1. , т.е. E_F ниже, чем на kT от дна Е_с.

, (8.18)

т.е. электроны подчиняются статистике Больцмана, а не Ферми-Дирака.

Это невырожденный полупроводник, электроны ведут себя как идеальный газ. С ростом Т растет и n по экспоненте.

2. , т.е. E_F лежит в глубине Е_с на 5kT .

Учтем (8.15)

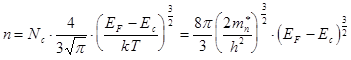(8.19)

Таким образом, концентрация n ¹ f(T) не зависит от Т, т.е. полупроводник является вырожденным. Поведение электронов аналогично поведению в металлах, т.е. концентрация постоянна и температура не влияет на нее.

3. – промежуточный случай.

В большинстве реальных случаев в полупроводниках реализуется невырожденное состояние (p-n переход, датчики, другие приборы).

Аналогично все для p-типа.