Комплексные числа, как векторы на плоскости

Пусть задано комплексное число 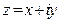. Отметим на плоскости точку с координатами, которые являются соответственно действительной и мнимой частями заданного комплексного числа. Множество комплексных чисел взаимно однозначно соответствует множеству точек

на этой плоскости. Построенную плоскость в этом случае называют комплексной плоскостью. Вспомним, что при сложении комплексных чисел действительная и мнимая части этих чисел складываются, при вычитании комплексных чисел действительная и мнимая части этих чисел вычитаются, при умножении комплексных чисел на действительное число действительная и мнимая части этих чисел умножаются на это число. Но именно так и происходят действия с обычными геометрическими векторами. В этом и заключается геометрический смысл указанных операций над комплексными числами.

Более того, в некоторых книгах вы можете встретить определение комплексных чисел, как пары действительных чисел с соответствующим образом введенными операциями сложения и умножения. Такое определение эквивалентно данному в этой лекции.

Тригонометрическая форма записи комплексных чисел

Давайте еще раз посмотрим на комплексную плоскость и заметим, что справедливы равенства: 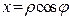, . Следовательно, для комплексного числа 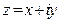справедливо равенство . Запись комплексного числа в виде является представлением комплексного числа в тригонометрической форме. При этом число называется модулем комплексного числа, а число 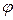или угол 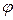называется аргументом комплексного числа. Обычно используются обозначения 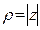, или . По поводу двух последних обозначений заметим, что аргумент комплексного числа определяется неоднозначно. Если вектор повернуть на угол, кратный , вокруг начала координат в любом направлении, то точка переходит сама в себя. Запись 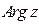используется для всего набора таких аргументов, а вот запись означает конкретное «главное» значение аргумента комплексного числа, лежащее на промежутке 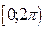(или ).

Геометрический смысл умножения и деления комплексных чисел

Пусть заданы 2 комплексных числа 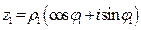и . Найдем произведение этих двух чисел 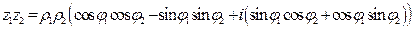. С учетом известных тригонометрических формул «синус суммы» и «косинус суммы» эта формула запишется в виде 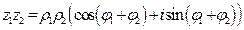. Итак, при перемножении комплексных чисел модули этих чисел перемножаются, а аргументы складываются.

Так как деление является действием, обратным к умножению, то справедлива формула . Итак, при делении комплексных чисел модули этих чисел делятся, а аргументы вычитаются.