Интегрирование функций

2016-09-16

468

Обсуждений (0)

0.00 из 5.00 0 оценок

Некоторые задачи вычислительной математики

Решение задач линейной алгебры.

Пусть A – квадратная матрица.

Для вычисления определителя предназначена встроенная функция det:

D = det(A)

Для нахождения обратной матрицы служит встроенная функция inv:

A1 = inv(A)

Для того чтобы задать в MATLAB систему линейных уравнений необходимо ввести основную матрицу системы и вектор правой части , например, для системы

основная матрица системы:

>> A = [1 2 1 4; 2 0 4 3; 4 2 2 1; -3 1 3 2]

вектор правой части:

>> B = [13; 28; 20; 6]

Решение системы линейных алгебраических уравнений в MATLAB можно выполнить при помощи символа \ .

Решение системы:

>> X = A\B

X =

-1

Проверка

>> A *X

В результате должны получить вектор B.

ans =

13.0000

28.0000

20.0000

6.0000

Интегрирование функций

Вычисление определенных интегралов

В MatLab существует встроенная функция, реализующая алгоритм метода Симпсона с автоматическим выбором шага

I = quad('имя функции', а, b)

где

имя функции – имя функции, задающей подынтегральное выражение;

а, b – пределы интегрирования,

I – значение интеграла.

Для повышения точности вычислений следует задать дополнительный четвертый аргумент e – точность метода:

I = quad('name', а, b, e).

Например, требуется вычислить определенный интеграл

Подынтегральную функцию можно вводить разными способами:

Первый способ.

Создаем файл-функцию, для вычисления подынтегрального выражения и сохраняем её, например, под именем fint

------------------------------------------------------------------------------------------------------------------------

function f = fint(x)

f = exp(-x).*sin(x);

------------------------------------------------------------------------------------------------------------------------

Затем, например, в командном окне выполним команду

>> I = quad('fint', -1, 1)

Выведем результат в формате long

I =

-0.66349146785310

Для повышения точности вычислений следует задать дополнительный четвертый аргумент:

>> I = quad('fint', -1, 1, 1.0e-10)

I =

-0.66349366663001

Второй способ.

Подынтегральную функцию можно вводить и как строку, используя команду inline:

>> F = inline('exp(-x).* sin(x)')

F =

Inline function:

F(x) = exp(-x).* sin(x)

Далее вызываем встроенную функцию quadс тремя входными аргументами, при этом имя функции пишется без апострофов:

>> I = quad(F, -1, 1)

I =

-0.66349146785310

Третий способ.

Подынтегральную функцию можно вводить, используя символ @:

>> F = @(x)exp(-x).*sin(x)

F =

@(x)exp(-x).*sin(x)

>> I = quad(F, -1, 1)

I =

-0.6635

Вычисление интегралов, зависящих от параметра.

Пусть требуется вычислить интеграл

где x – независимая переменная, и – параметры. Вычислим этот интеграл при значениях параметров

и .

Первый способ.

Создаем файл-функцию, зависящую от трех входных аргументов:

------------------------------------------------------------------------------------------------------------------------

function f = fparam(x, par1, par2)

f = par1.*x.^2+par2.*sin(x);

------------------------------------------------------------------------------------------------------------------------

Для вычисления интеграла используем quad, в командном окне

I = quad('fparam', -1, 1, 1.0e-06 , 0, 22.5, -5.9)

I =

При вычислении интеграла, зависящего от параметров, их следует указывать, начиная с шестого аргумента quad.

( Цифра ''0'' на месте пятого аргумента подавляет вывод узлов интегрирования на экран)

Второй способ.

Подынтегральную функцию вводим как строку

>> F = inline('par1.*x.^2+par2.* sin(x)','x','par1','par2')

F =

Inline function:

F(x,par1,par2) = par1.*x.^2+par2.* sin(x)

Затем снова используем quad в виде

>> I = quad(F, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Третий способ.

>> f = @(x, par1, par2) par1.*x.^2+par2.* sin(x)

f =

@(x,par1,par2)par1.*x.^2+par2.*sin(x)

>> I = quad(f, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Вычисление интегралов от функций, заданных в виде таблицы.

Пусть функция задана таблицей своих значений в точках , ( – четное) с постоянным шагом :

		………………..
		………………..

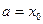
Формула Симпсона для численного интегрирования имеет вид

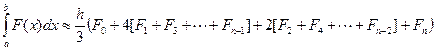Напишем М-функцию f_simps, реализующую алгоритм метода Симпсона в MatLab

Здесь: F – вектор значений табличной функции, M – четное число интервалов на которые разделён отрезок , h – шаг таблицы.

Например, для функции создадим таблицу, разделяя отрезок на 10 интервалов и для полученной табличной функции вычислим приближенное значение интеграла , используя функцию f_simps.

Выполняем в команды:

M = 10;

a = -1;

b = 1;

h = (b-a)/M;

x = a:h:b;

F = exp(-x).*sin(x);

Int = f_simps(F, M, h)

Int =

-0.6635

Приближение функций

1. Многочлены.

Многочлен в MatLab задается вектором его коэффициентов. Например, введем многочлен

p = [1 0 3.2 -5 .2 0 0.5 1 -3]

Значение многочлена в точке

вычисляет команда polyval, например, в точке :

polyval(p, 1)

Аргумент может быть матрицей или вектором, при этом результат также будет матрицей или вектором.

2. Интерполяционный многочлен.

Пусть задана сеточная функция

x			…..
y			…...

и требуется приблизить эту сеточную функцию многочленом

удовлетворяющим условиям интерполяции:

Коэффициенты интерполяционного многочлена 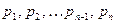– решение системы линейных уравнений

Матрица этой системы представляет собой, так называемую матрицу Вандермонда, которая в MatLabзадается функцией vander.Неизвестные коэффициенты 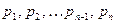можно найти путем левого матричного деления «\».

Например, построим интерполяционный многочлен для заданной таблицы

	0,5
	1,5				1,2

и вычислим приближенное значение при .

Создадим М-файл list_12.

В результате работы программы получим графики табличной функции и интерполяционного многочлена:

и вывод в командном окне

ТАБЛИЦА

0.5 1 2 3 4

1.5 0 1 2 1.2

ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН P_4

0.21905 -2.4905 9.4667 -13.252 6.0571

ЗНАЧЕНИЕ МНОГОЧЛЕНА В ТОЧКЕ x_0 = 3.5

P_x_0 =

1.7321

3. Кусочно-многочленная интерполяция.

1) Интерполяция по соседним элементам

– способ интерполяции данных, при которой значения в каждой промежуточной точке принимается равным ближайшему значению, заданному в таблице.

2) Линейная интерполяция

– это способ, при котором соседние точки соединены отрезками прямых.

3) Интерполяция сплайнами.

Все эти способы интерполяции реализуются встроенной функцией interp1.

yi = interp1(x, y, xi, ’method’)

x – массив абсцисс табличной функции;

y – массив ординат табличной функции;

xi – промежуточные точки, в которых необходимо вычислить значения интерполирующей функции;

Параметр method может принимать одно из следующих значений:

nearest – интерполяция по соседним элементам;

liner– линейная интерполяция;

spline– интерполяция кубическим сплайном.

Выходным аргументом interp1 является вектор yi значений интерполирующей функции.

Рассмотрим таблицу из предыдущего примера и построим для неё различные интерполирующие функции. Текст программы приведем в list_13.

Графики

Вывод в командное окно

ТАБЛИЦА

0.5 1 2 3 4

1.5 0 1 2 1.2

ЗНАЧЕНИЕ ИНТЕРП. ФУНКЦИЙ В ТОЧКЕ x_0 = 3,5

Near_x_0 =

1.2

Line_x_0 =

1.6

Spline_x_0 =

1.8618

ynear_X1 = 1

4. Метод наименьших квадратов.

Пусть некоторая функция задана своими табличными значениями в п различных точках ( ).

		………………..
		………………..

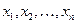Требуется найти многочлен степени

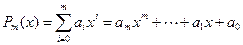коэффициенты которого минимизируют функцию

Построение полинома, который приближает функцию, заданную таблицей, по методу наименьших квадратов в MatLab осуществляется при помощи polyfit:

pk = polyfit(x, y, k),

x – массив абсцисс экспериментальных точек;

y – массив ординат экспериментальных точек;

k – степень аппроксимирующего полинома.

Результатом работы функции является массив pk коэффициентов полинома. Для того чтобы вычислить значение аппроксимирующего полинома в любой точке применяют функцию

Pk = polyval(pk, t),

где t – точка (или массив точек) в которой необходимо вычислить значение многочлена.

Например, для заданной таблицы