 |
Главная |
Разработка алгоритма решения задачи
|
из
5.00
|
На рис. 8 показан укрупненный алгоритм решения поставленной задачи. На рис. 9 - 12 показаны основные шаги поэтапной детализации основного алгоритма.


Следует обратить внимание на нумерацию блоков в детализирующих блок-схемах. Число до первой точки является номером детализируемого блока в основной схеме. Число после первой точки является номером блока в схеме детализации первого уровня и т.д.
Входы в детализирующие блок-схемы и выходы из них показаны окружностями с номерами блоков — источников информации и получателей результатов.
Значком & на рис. 11 обозначена логическая операция И.




Пример 3

Поскольку тестирование вручную алгоритма решения задачи о шахматном коне было бы достаточно громоздким, рассмотрим технологию тестирования на примере алгоритма Евклида (рис. 14).
Для тестирования вручную следует оставить достаточно свободного места справа от блок-схемы. Контрольный пример не должен быть слишком сложным - это затрудняет тестирование, но и не быть тривиальным - это может привести к случайному совпадению с правильным решением. В первом столбце таблицы справа от блок-схемы, записываются переменные или условия, значения которых могут изменяться. Начиная со второго столбца сверху-вниз записываются результаты выполнения алгоритма. Начало нового цикла соответствует добавлению нового столбца таблицы. Исполнитель (разработчик алгоритма) должен выполнять команды формально, строго придерживаясь предписаний в блок-схеме.
Задание
Разработать алгоритм и программу решения задачи, Задачу выбрать в разделе «Варианты заданий к работе» согласно вашему варианту. Оформить отчет о работе.
Порядок выполнения
1) Внимательно ознакомиться с теоретическими сведениями, приведенными в лабораторной работе;
2) Выбрать задание из раздела «Варианты заданий к работе», с номером равным вашему варианту;
3) Последовательность решения задачи (оформляется в рукописном виде):
- Произвести словесную формулировку задачи;
Пример: Вычислить наибольший общий делитель (НОД) двух натуральных чисел A и B, используя алгоритм Евклида.
- Формализовать поставленную задачу, указав, что дано в задаче и что нужно найти;
Пример:
Дано: A, B.
Найти: НОД.
- Составить контрольный пример для тестирования задачи;
Пример: A = 35; B = 14; НОД = 7.
- Произвести словесное описание алгоритма;
Пример:
1. Ввод А и В;
2. Если А = В, то Переход к 7, иначе Переход к 3;
3. Если А > В, то Переход к 4, иначе Переход к 5;
4. А = А – В;
5. В = В – А;
6. Переход к 2;
7. Вывод «НОД=А».
- Нарисовать блок-схему алгоритма решения задачи;
Пример:
- Нарисовать таблицу с тестом алгоритма справа от блок-схемы 
. Таблица составляется согласно следующим правилам:
а). Строки располагаются напротив соответствующих операций в блок-схеме;
б). Первый столбец должен содержать имена переменных или логическое условие, соответствующее операции в блок-схеме;
в). Остальные столбцы должны содержать значения переменных или результат логического выражения для каждой случая выполнения данной операции в блок-схеме;
Пример:

| A B A=B A>B B A НОД | нет да | |||
| нет да | нет нет | да | |||
4) Продемонстрировать составленную последовательность решения задачи преподавателю, получить отметку о выполнении и оформить отчет в электронном виде;
Содержание отчета
1) Титульный лист, оформленный согласно применяемому ранее шаблону;
2) Цель лабораторной работы;
3) Ход работы с результатами выполнения пункта 3 раздела «Порядок выполнения».
Контрольные вопросы
1) Что такое программа?
2) Что понимают под исполнителем?
3) Что представляет собой машинный код?
4) Что такое транслятор? Перечислите типы трансляторов.
5) Как работает интерпретатор? В чем его достоинства?
6) В чем заключается достоинство компиляторов?
7) Какие компоненты необходимы для создания программ? Каково назначение каждого из этих компонентов?
8) Что называется интегрированной системой программирования?
9) Чем характеризуются системы визуального программирования?
10) Какие подходы по способу разработки программ можно выделить? Охарактеризуйте каждый подход.
11) Каковы основные системы программирования?
12) Перечислите основные этапы развития языков программирования.
13) Что понимают под алгоритмом?
14) Каковы способы записи алгоритмов?
15) В чем заключаются основные свойства алгоритма?
16) Перечислите основные алгоритмические структуры и опишите их.
17) Каковы основные принципы разработки алгоритмов?
18) Назовите основные этапы составления алгоритмов.
19) Приведите пример, реализующий этапы алгоритмизации.
20) Каковы основные этапы решения задач с помощью ЭВМ? Дайте характеристику каждому этапу.
Варианты заданий к работе
Задача 1
Вычислить выражение

Задача 2
Элементы x иy вычисляются по формулам:

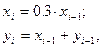
при  Вычислить
Вычислить  .
.
Задача 3
Вычислить выражение

Задача 4
Вычислить выражение:

Задача 5
Вычислить выражение

Задача 6
Значения членов числовой последовательности ai , bi вычисляются по формулам:
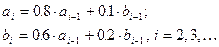
Не применяя массивов, вычислить  при а1 = b1 = 1.
при а1 = b1 = 1.
Задача 7
Элементы последовательности xi,  вычисляются по формуле
вычисляются по формуле
 при x1 = 2 и x2 = 1. Вычислить
при x1 = 2 и x2 = 1. Вычислить  .
.
Задача 8
Вычислить сумму
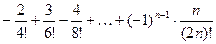
Задача 9
Значения xi вычисляются циклически:

Вычислить xk, не применяя массивов, если 
Задача 10
Вычислить выражение:

Задача 11
Вычислить выражение
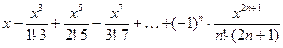
Задача 12
Вычислить произведение первых N сомножителей:
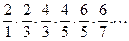
Задача 13
Числовая последовательность задана формулой

Вычислить  , не применяя массивов, если
, не применяя массивов, если 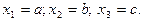
Задача 14
Вычислить выражение:

Задача 15
Вычислить выражение

Задача 16
Вычислить приближенное значение бесконечной суммы
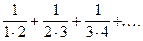
Нужное приближение считается полученным, если последнее слагаемое, вошедшее в сумму, оказалось меньше данного положительного  .
.
Задача 17
Вычислить приближенно значение бесконечной суммы

Нужное приближение считается полученным, если последнее слагаемое, вошедшее в сумму, оказалось меньше данного положительного  .
.
Задача 18
Числовая последовательность задана формулой

Определить, начиная с какого i, члены последовательности становятся меньше данного положительного числа  .
.
Задача 19
Числовая последовательность задана формулой

Определить минимальное количество членов k, для которых выполняется условие 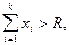 где R - заданное число,
где R - заданное число, 
Задача 20
Дано действительное b<0. Последовательность a1, a2, ... образуется по следующему закону:

Не используя массивов, найти значение и номер первого неотрицательного члена последовательности.
Задача 21
Члены последовательности вычисляются по формуле

Найти номер i, начиная с которого выполняется условие  .
.
Задача 22
Сколько членов последовательности  надо просуммировать, чтобы сумма превысила данное значение S>0?
надо просуммировать, чтобы сумма превысила данное значение S>0?
Задача 23
Дана последовательность: 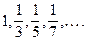 Сколько членов этой последовательности, начиная с первого, и, далее по порядку, надо перемножить, чтобы произведение оказалось меньше данной положительной величины
Сколько членов этой последовательности, начиная с первого, и, далее по порядку, надо перемножить, чтобы произведение оказалось меньше данной положительной величины  e?
e?
Задача 24
Вычислить приближенное значение бесконечной суммы

Нужное приближение считается полученным, если абсолютное значение последнего слагаемого, вошедшего в сумму, оказалось меньше данного положительного  .
.
Задача 25
Среди чисел  найти ближайшее меньшее, чем заданное число A.
найти ближайшее меньшее, чем заданное число A.
Задача 26
Последовательность чисел формируется по следующему закону:  Найти номер i (i³2) первого члена последовательности, для которого выполняется условие
Найти номер i (i³2) первого члена последовательности, для которого выполняется условие 
Задача 27
Элементы последовательности xi,  вычисляются по формуле
вычисляются по формуле  при x1 = 2 и x2 = 1. Вычислить, не применяя массивов, начиная с какого i xi становится меньше заданного значения Z, (0<Z<1.3).
при x1 = 2 и x2 = 1. Вычислить, не применяя массивов, начиная с какого i xi становится меньше заданного значения Z, (0<Z<1.3).
Задача 28
Значения членов числовой последовательности ai , bi вычисляются по формулам:

где i = 2, 3, ...; а1 = b1 = 1.
Вычислить, не применяя массивов, начиная с какого i bi становится меньше заданного значения S>0.
Задача 29
Последовательность значений имеет вид:

При каком минимальном n значение произведения членов последовательности от 1-го до n-го становится больше заданного P>0?
Задача 30
Последовательность значений имеет вид:

При каком минимальном n значение произведения первых членов последовательности от 1-го до n-го становится меньше заданного 0<P<1?
|
из
5.00
|
Обсуждение в статье: Разработка алгоритма решения задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

