 |
Главная |
Одноканальная СМО с очередью
|
из
5.00
|
Пусть на вход одноканальной СМО (n = 1 - число каналов, m - число мест в очереди) поступает экспоненциальный поток заявок. Время обслуживания заявки в СМО - случайная величина, распределенная по экспоненциальному закону.
Интенсивность потока заявок на входе СМО равна λ (1/сек).
Среднее время обслуживания заявки обозначим - tобсл. Обратная величина к среднему времени обслуживания определяет интенсивность потока обслуживания μ = 1/ tобсл. Эта величина характеризует среднее число заявок, которое может обслужить система в единицу времени.
Определим состояния СМО Si :
S0 - система свободна, заявок нет, очереди нет;
S1 - система обслуживает одну заявку, очереди нет;
S2 - система обслуживает одну заявку, в очереди одна заявка;
…………………………………………
S m+1 - система обслуживает одну заявку, в очереди - m заявок.
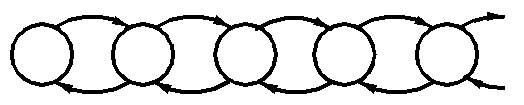 λ λ λ λ λ
λ λ λ λ λ
S0 S1 S2 S3 S4
μ μ μ μ μ
Рис. 3. Граф состояний одноканальной СМО с очередью
Верхние стрелки на этом графе показывают процесс прихода заявок, нижние стрелки - процесс обслуживания заявок.
Запишем уравнения Колмогорова для этой системы
 |
После решения первых уравнений системы, получим
 |
Подставим эти вероятности в последнее условие, получим

Из этой формулы находим p0
 |
Коэффициент загрузки и коэффициент простоя СМО. Вероятность p0 соответствует состоянию S0, а это по определению вероятность того, что система свободна и не обслуживает ни одной заявки. Тогда p0 - вероятность простоя СМО, или коэффициент простоя. Поэтому величина pзаг = 1 - p0 - вероятность загрузки СМО или коэффициент загрузки.
СМО с бесконечной очередью.
 Пусть очередь в СМО бесконечна (m = 8). Тогда знаменатель в предыдущей формуле для p0 является геометрической прогрессией. Если (λ/μ) < 1, то ряд сходится и его сумма равна
Пусть очередь в СМО бесконечна (m = 8). Тогда знаменатель в предыдущей формуле для p0 является геометрической прогрессией. Если (λ/μ) < 1, то ряд сходится и его сумма равна
 Это позволяет записать выражение для вероятности p0. Это коэффициент простоя.
Это позволяет записать выражение для вероятности p0. Это коэффициент простоя.
Тогда коэффициент загрузки равен
 |
Вероятность отказа. В СМО с конечной очередью существует вероятность состояния, в котором очередная пришедшая заявка не может быть обслужена. Это последнее состояние Sm+1. Поэтому вероятность отказа pотк равен вероятности пребывания СМО в этом состоянии.
 |
В СМО с бесконечной очередью вероятность отказа равна нулю, если
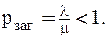 |
Замечание. Условие pзаг < 1 является фундаментальным в теории СМО. Если принять, что λ = μ или pзаг = 1, то вероятность отказа
 |
превышает единицу, что делает СМО неработоспособной.
 Пропускная способность СМО. Для СМО с любой структурой пропускная способность А - количество обслуженных заявок, покидающих систему, в единицу времени. Пропускная способность равна количеству входящих заявок в единицу времени, умноженное на вероятность того, что заявка будет обслужена
Пропускная способность СМО. Для СМО с любой структурой пропускная способность А - количество обслуженных заявок, покидающих систему, в единицу времени. Пропускная способность равна количеству входящих заявок в единицу времени, умноженное на вероятность того, что заявка будет обслужена
Среднее число заявок, находящихся в СМО.
В системе с конечной очередью в каждый момент времени может быть одно из следующих состояний:
S0: в системе 0 заявок;
S1: в системе 1 заявка в канале обслуживания и 0 заявок в очереди;
S2: в системе 1 заявка в канале обслуживания и 1 заявка в очереди;
S3: в системе 1 заявка в канале обслуживания и 2 заявки в очереди;
……………………………………………………………………………
S m+1: в системе 1 заявка в канале обслуживания и m заявок в очереди;
Номер состояния S k соответствует числу k заявок, находящихся в СМО. Вероятность этого состояния равна pk.
Число заявок, находящихся в СМО, является дискретной случайной величиной со следующей функцией распределения вероятностей
| Значение с.в. | … | m + 1 | |||
| Вероятность pk | p0 | p1 | p2 | pn+1 |
 Среднее число заявок в СМО nср равно математическому ожиданию этой случайной величины
Среднее число заявок в СМО nср равно математическому ожиданию этой случайной величины
 или
или
 Для системы с бесконечной очередью ( m → ∞) эта формула превращается в убывающую геометрическую прогрессию. В этом случае среднее число заявок в СМО равно
Для системы с бесконечной очередью ( m → ∞) эта формула превращается в убывающую геометрическую прогрессию. В этом случае среднее число заявок в СМО равно
Среднее число обслуживаемых заявок. В канале обслуживания одноканальной СМО может обслуживаться одна заявка или ни одной заявки. Этому соответствует следующая дискретная случайная величина
| Значение с.в. | ||
| Вероятность pk | p0 | p1 |
Среднее число обслуживаемых заявок nоз равно математическому ожиданию этой случайной величины

 Средняя длина очереди. Средняя длина очереди rcp равна среднему числу заявок в системе nср за вычетом среднего числа обслуживаемых заявок.
Средняя длина очереди. Средняя длина очереди rcp равна среднему числу заявок в системе nср за вычетом среднего числа обслуживаемых заявок.
 В одноканальной СМО с бесконечной очередью средняя длина очереди равна
В одноканальной СМО с бесконечной очередью средняя длина очереди равна
Средняя длина очереди резко возрастает при стремлении коэффициента загрузки pзаг к единице.

Для pзаг больше единицы работа СМО невозможна.
Замечание. Мы рассматриваем только практически значимый стационарный режим работы СМО, в котором переходные вероятности перестают зависеть от времени и система может работать сколь угодно долго. Для исследования переходного режима необходимо численно решить систему дифференциальных уравнений Колмогорова и проанализировать графики изменения переходных вероятностей во времени, как это было показано выше.
Среднее время пребывания заявки в СМО. В стационарном режиме работы СМО ( pзаг <1 ) интенсивности входного и выходного потоков равны между собой и равны λ. Пусть в стационарном режиме среднее число заявок в системе в единицу времени равно nср. Тогда согласно теореме Литтла среднее время пребывания заявки в СМО - Tсист равно
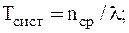 |
Теорема Литтла доказана для любого распределения потока заявок и при любом распределении времени обслуживания.
 Для СМО с бесконечной очередью эту формулу можно переписать в следующем виде
Для СМО с бесконечной очередью эту формулу можно переписать в следующем виде
Аналогично можно записать формулу для среднего времени пребывания заявки в очереди Tоч. В общем случае
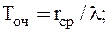 |
Для СМО с бесконечной очередью получим
 |
Эти формулы позволяют определить среднее время обслуживания заявки СМО - tобсл из следующего соотношения
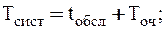 |
|
из
5.00
|
Обсуждение в статье: Одноканальная СМО с очередью |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

