 |
Главная |
Cильное затухание (апериодический режим)
|
из
5.00
|
Виды трения
Трение покоя проявляется в том случае, если тело находившееся в состоянии покоя, приводится в движение. Коэффициент трения покоя обозначается μ0.
Трение скольжения проявляется при наличии движения тела, и оно значительно меньше трения покоя. μск< μ0
Трение качения проявляется в том случае, когда тело катится по опоре, и оно значительно меньше трения скольжения. μкач<<μск. Сила трения качения зависит от радиуса  катящегося предмета. В типичных случаях (при расчетах трения качения колес поезда или автомобиля), когда радиус колеса известен и постоянен, его учитывают непосредственно в коэффициенте трения качения μкач.
катящегося предмета. В типичных случаях (при расчетах трения качения колес поезда или автомобиля), когда радиус колеса известен и постоянен, его учитывают непосредственно в коэффициенте трения качения μкач.
Определение коэффициента трения. Коэффициент трения можно определить экспериментально. Для этого помещают тело на наклонную плоскость, и определяют угол наклона при котором:
- коэффициент трения покоятело начинает двигаться
(коэффициент трения покоя μ0)
- коэффициент трения скольжениятело движется с постоянной скоростью(коэффициент трения скольжения μ). μFн=FсμGcos(α)=Gsin(α) μ=tg(α)
Здесь: μ — искомый коэффициент трения, α — угол наклона плоскости
- Уравнение Мещерского.
Мещерскогоуравнение (по имени И. В. Мещерского), дифференциальное уравнение движения точки переменной массы, является основным уравнением механики тел переменной массы.

- Формула Циолковского.
Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической. 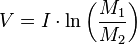 где:
где:  — конечная (после выработки всего топлива) скорость летательного аппарата;
— конечная (после выработки всего топлива) скорость летательного аппарата;  — удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива);
— удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива);  — начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо);
— начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо);  — конечная масса летательного аппарата (полезная нагрузка + конструкция).
— конечная масса летательного аппарата (полезная нагрузка + конструкция).
Эта формула была выведена К. Э. Циолковским в рукописи «Ракета» 10 мая 1897 года (22 мая по григорианскому календарю).[1]
Однако первыми уравнение движения тела с переменной массой решили английские исследователи У. Мур, а также П. Г. Тэйт и У. Дж. Стил из Кембриджского университета соответственно в 1810—1811 гг. и в 1856 году.
Формула Циолковского может быть получена путём интегрирования дифференциального уравнения Мещерского для материальной точки переменной массы:  в котором
в котором  — масса точки;
— масса точки;  — скорость точки;
— скорость точки;  — относительная скорость, с которой движется отделяющаяся от точки часть её массы. Для ракетного двигателя эта величина и составляет его удельный импульс
— относительная скорость, с которой движется отделяющаяся от точки часть её массы. Для ракетного двигателя эта величина и составляет его удельный импульс 
Для многоступенчатой ракеты конечная скорость рассчитывается как сумма скоростей, полученных по формуле Циолковского отдельно для каждой ступени, причем при расчёте характеристической скорости каждой ступени к её начальной и конечной массе добавляется суммарная начальная масса всех последующих ступеней.
Введем обозначения:  — масса заправленной
— масса заправленной  -ой ступени ракеты;
-ой ступени ракеты;  — масса
— масса  -ой ступени без топлива;
-ой ступени без топлива;  — удельный импульс двигателя
— удельный импульс двигателя  -ой ступени;
-ой ступени;  — масса полезной нагрузки;
— масса полезной нагрузки;  — число ступеней ракеты.
— число ступеней ракеты.
Тогда формула Циолковского для многоступенчатой ракеты может быть записана в следующем виде:

- Принцип относительности Галилея. Координаты, скорость, ускорение при переходе в другую ИСО.


- Не ИСО. Пример силы инерции.
Неинерциа́льнаясисте́маотсчёта — системаотсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью.




- Свойства сил инерции.
Следует отчетливо понимать, что силы инерции нельзя ставить в один ряд с такими силами, как упругие, гравитационные силы и силы трения, т. е. силами, обусловленными воздействием на тело со стороны других, тел. Сиды инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. В этом смысле их можно назвать фиктивными силами.
Введение в рассмотрение сил инерции не является принципиально необходимым. В принципе любое движение можно всегда рассмотреты по отношению к инерциальной системе отсчета. Однако практически часто представляет интерес как раз движение тел по отношению к неинерциальным системам отсчета, например по отношению к земной новерхности.
Использование сил инерции даёт возможность решить соответствующую задачу непосредственно по отношению к такой системе отсчета, что часто оказывается значительно проще, чем рассмотрение движения в инерциальной системе.
Характерным свойством сил инерции является их пропорциональность массе тела. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения. Представим себе, что мы находимся в удаленной от всех внешних тел закрытой кабине, которая движется с ускорением g в направлении, которое мы назовем «верхом» (рис. 32.2). Тогда все тела, находящиеся внутри кабины, будут вести себя так, как если бы на них действовала сила инерции —mg. В частности, пружина, к концу которой подвешено тело массы  , растянется так, чтобы упругая сила уравновесила силу инерции —mg. Однако такие же явлений наблюдались бы и в том случае, если бы кабина была неподвижной и находилась вблизи, поверхности Земли. Не имея возможности «выглянуть» за пределы кабины, никакими опытами, проводимыми внутри кабины, Мы не смогли бы установить чем обусловлена сила —mg ускоренным движением кабины или действием гравитационного поля Земли. На этом основании сворят об эквивалентности сил инерции и тяготения. Эта эквивалентность лежит в обиове общей теории относительности Эйнштейна.
, растянется так, чтобы упругая сила уравновесила силу инерции —mg. Однако такие же явлений наблюдались бы и в том случае, если бы кабина была неподвижной и находилась вблизи, поверхности Земли. Не имея возможности «выглянуть» за пределы кабины, никакими опытами, проводимыми внутри кабины, Мы не смогли бы установить чем обусловлена сила —mg ускоренным движением кабины или действием гравитационного поля Земли. На этом основании сворят об эквивалентности сил инерции и тяготения. Эта эквивалентность лежит в обиове общей теории относительности Эйнштейна.
- Полная механическая энергия.
ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Изменение кинетической энергии частицы будет определяться работой консервативных и неконсервативных сил:
Aконс + Aнеконс = K2 – K1= ?K (1)
а изменение потенциальной энергии будет обусловлено только работой консервативных сил:Aконс = U1 – U2 = –?U. (2)
Тогда, подставляя (2) в (1), получим?K+ ?U = ?(K + U) = Aнеконс. (3)
Из анализа формулы (3) следует, что работа неконсервативных сил идет на приращение суммы кинетической и потенциальной энергий частицы, которую называют полной механической энергией и обозначают буквой E, т. е.E= K + U. (4)
Итак, из (3) и (4) следует, что приращение полной механической энергии частицы на конечном перемещении из точки 1 в точку 2 равно работе неконсервативных сил:
?E= E2 – E1 = Aнеконс, (5)
где E1 и E2 – полные механические энергии частицы в точках 1 и 2 соответственно.
Формула (5) выражает закон изменения полной механической энергии частицы: приращение полной механической энергии частицы на некотором пути равно алгебраической сумме работ всех неконсервативных сил, действующих на частицу на том же пути.
Если Анеконс> 0, то полная механическая энергия частицы увеличивается, если же Анеконс< 0, то уменьшается.
Из закона изменения полной механической энергии частицы следует закон сохранения этой величины: если на частицу не действуют неконсервативные силы или работа неконсервативных сил на любом перемещении при переходе частицы из точки 1 в точку 2 равна нулю, то полная механическая энергия частицы сохраняется
(E1 = E2 = E = const), т. е.
E= K + U = const. (6)
Выражение (6), в частности, означает, что если на частицу действуют только консервативные силы, то сохраняется сумма кинетической и потенциальной энергий, однако при этом может происходить превращение потенциальной энергии в кинетическую и наоборот.
Закон сохранения полной механической энергии в форме (6) может быть записан и для системы частиц, не взаимодействующей с внешними телами, при условии, что в системе действуют только консервативные силы. Закон сохранения энергии остается инвариантным (форма его записи остается той же самой) при изменении начала отсчета времени. Это является следствием однородности времени.
- Кинетическая энергия.


- Консервативные и диссипативные силы в механике.

- Связь кинетической энергии и работы.
Работа – мера изменения энергии(физический смысл работы).
Теорема о кинетической энергии: работа всех сил приводит к изменению кинетической энергии теле (или системы тел)
 .
.
Работа потенциальной силы, приводящая к изменению конфигурации системы, равна приращению потенциальной энергии, взятому со знаком минус:
 .
.
- Связь консервативной силы и потенциальной энергии.

- Закон сохранения полной механической энергии.

- Закон сохранения импульса.
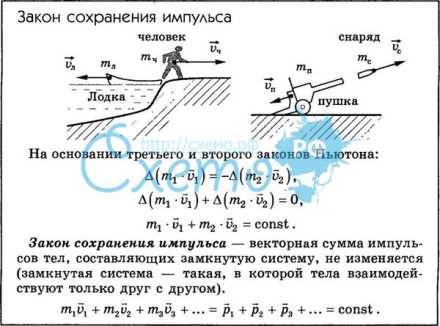


- Понятие центра масс.
Определение
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом[2]:

где 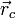 — радиус-вектор центра масс,
— радиус-вектор центра масс,  — радиус-вектор i-й точки системы,
— радиус-вектор i-й точки системы,  — массаi-й точки.
— массаi-й точки.
Для случая непрерывного распределения масс:


где  — суммарная масса системы,
— суммарная масса системы,  — объём,
— объём,  — плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.
— плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.
Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами  , то радиус-вектор центра масс такой системы
, то радиус-вектор центра масс такой системы  связан с радиус-векторами центров масс тел
связан с радиус-векторами центров масс тел  соотношением[3]:
соотношением[3]:

Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.

- Момент силы, момент импульса.



- Закон сохранения момента импульса.
Зако́нсохране́ниямоме́нтаи́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде:  , если система находится в равновесии.
, если система находится в равновесии.
- Момент инерции.


- Теорема Штейнера.


- Кинетическая энергия вращающегося и катящегося тела.
Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m1, m2,..., mn , находящиеся на расстоянии r1, r2,..., rn от оси.
При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами mi опишет окружность соответствующих радиусов ri; при этом объем будет иметь соответствующую линейную скорость vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
 (1)
(1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
 или
или 
Используя выражение (1), получаем

где Jz - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
 (2)
(2)
Из сравнения формулы (2) с выражением для кинетической энергии поступательно движущегося тела (T=mv2/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула (2) справедлива для тела вращающегося вокруг неподвижной оси.
В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:

где m - масса катящегося тела; vc - скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.
- Уравнение динамики вращательного движения.

- Коэффициент упругости. Модуль Юнга.
Коэффицие́нтупру́гости (иногда называют коэффициентом Гука, коэффициентом жёсткости или жёсткостью пружины) — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой k[1], иногда D[2] или c[3]. Имеет размерность Н/м или кг/с2 (в СИ), дин/см или г/с2 (в СГС).
Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:

где:E — модуль упругости,F — сила,S — площадь поверхности, по которой распределено действие силы,l — длина деформируемого стержня,  — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
— модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
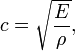 где
где  — плотность вещества.
— плотность вещества.
- Напряжение.
Напряжение - это физическая величина, обозначающая внутренние силы, возникающие в теле под влиянием внешнего воздействия 
- Энергия упругой деформации.
Деформированное тело может совершить работу, так как оно обладает запасом потенциальной энергии, называемой упругой энергией. Она равна работе сил, затраченной на деформацию тела, не увеличивая его кинетической энергии. Для соблюдения последнего, деформацию надо производить достаточно медленно, постепенно увеличивая приложенную силу так, чтобы в любой момент времени каждая часть тела находилась в равновесии. При этом говорят, что процесс деформации является квазистатическим.
Вычислим теперь энергию упругой деформации стержня. Приложим к стержню растягивающую силу f(x) и медленно увеличим от начального значения f=0 до конечного f=F . При этом удлинение стержня будет меняться от x=0 до x=∆l . По закону Гука f(x)=kx , где k – коэффициент упругости, который помимо материала стержня зависит также от формы и размеров тела: 
 (16.4)
(16.4)
При квазистатической деформации стержня вся работа силы f переходит в приращение упругой энергии стержня:
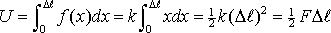
 , (16.5)где F
, (16.5)где F  – конечное значение деформирующей силы.
– конечное значение деформирующей силы.
Если бы стержню сразу приложили постоянную силуF , то при удлинении стержня на ∆l , совершалась бы вдвое больше работы: A=F∆l . Но упругая энергия стержня все равно выражается формулой (16.5) и составляет ровно половину совершенной работы. Вторая половина расходуется на увеличение кинетической энергии упругих колебаний и волн, которые возбуждаются в стержне из-за неквазистатичности процесса деформации.
Энергия упругой деформации распределена по всему объему тела. Энергияw, приходящая на единицу объема тела, называемая объемной плотностью упругой энергии, равна:

 (16.6)
(16.6)
Пользуясь законом Гука, эту формулу можно привести к виду  (16.7)
(16.7)
Под действием приложенной силы изменяются не только продольные, но и поперечные размеры стержня. Если поперечный размер стержня равен b, который при деформации получил приращение ∆b , то величина - ∆b/b называется относительным поперечным сжатием стержня. Отношение относительного поперечного сжатия к соответствующему продольному удлинению называется коэффициентом Пуассона (1781-1840):  (16.8)
(16.8)
Заметим, что ∆b и ∆ l всегда имеют противоположные знаки – при растяжении ∆ l>0 , ∆b <0 , а при сжатии – наоборот. Так что коэффициент Пуассона – положительная величина, зависит только от материала тела и является важной характеристикой упругих свойств тела. Можно показать, что всегда μ<1/2 .
Основным видом малых деформаций является растяжение (и сжатие), поэтому модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства тел. Все прочие коэффициенты и модули упругости могут быть выражены через постоянные E и μ.
- Параметры гармонических колебаний.





- Дифференциальное уравнение свободных незатухающих колебаний и его решение. График зависимости x(t).
Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.В качестве примера рассмотрим колебания тела, подвешенного на невесомой пружине, возникающие после того, как тело отклонили вниз, а затем отпустили (рис. 1.2 Колебания тела на пружине).
Со стороны растянутой пружины на тело действует упругая сила F, пропорциональная величине смещения х: F= - kx. (1.4)
Постоянный множитель k называется жесткостью пружины и зависит от ее размеров и материала. Знак «-» указывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т.е. к положению равновесия.При отсутствии трения упругая сила (1.4) - это единственная сила, действующая на тело. Согласно второму закону Ньютона (ma = F): 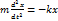
После переноса всех слагаемых в левую часть и деления на массу тела (m) получим дифференциальное уравнение свободных колебаний при отсутствии трения: 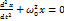 , (1.5) |
, (1.5) |  . (1.6) Решением этого уравнения является гармоническая функция
. (1.6) Решением этого уравнения является гармоническая функция 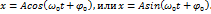
- Дифференциальное уравнение свободных затухающих колебаний и его решение. График зависимости x(t).
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).
Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)
 ,
,
где r – коэффициент сопротивления,  – скорость движения.
– скорость движения.
Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x:
 ,
,
где kx – возвращающая сила, rυx – сила трения. Это уравнение можно переписать:
 , отсюда следует:
, отсюда следует:  .
.
Введем обозначения:  .
.
Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так:  . (3.1.1)
. (3.1.1)
Решение уравнения (3.1.1) имеет вид (при  ):
): 
Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.
Найдем круговую частоту ω. Здесь она уже не равна 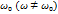 .
.
Для этого найдем первую и вторую производные от x:
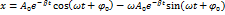
 ,
,
Подставим эти значения в (3.1.1) и сократим на  :
:

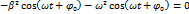
Сократим на  и выразим ω:
и выразим ω:
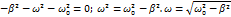 ,
,
где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение (3.1.1) будет только при .
Для колебаний под действием различных сил (квазиупругих) значения ω, β, ω0 будут различными. Например, для колебаний под действием упругой силы 
Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω – циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и  называется условным периодом затухающих колебаний.
называется условным периодом затухающих колебаний.
- Дифференциальное уравнение вынужденных колебаний. График зависимости x(t).
Øвывод уравнения вынужденных колебаний
Все реальные колебания являются затухающими. Чтобы реальные колебания происходили достаточно долго нужно периодически пополнять энергию колебательной системы, действуя на нее внешней периодически изменяющейся силой:  ; (84) где
; (84) где  - частота вынуждающей силы. Запишем уравнение динамики:
- частота вынуждающей силы. Запишем уравнение динамики:  ; (85)
; (85)
 ; (86)
; (86)
 ; (87)
; (87)

| дифференциальное уравнение второго порядка вынужденных гармонических колебаний. |
 (88)
(88)
Øрешение уравнения вынужденных колебаний
Решением уравнения (88) является уравнение:  (89)
(89)
При приложении внешней силы сначала возникает переходное состояние, при котором физическая система участвует одновременно в двух колебаниях, поэтому решением уравнения (88) будет выражение, состоящее из двух слагаемых:  (89), где
(89), где  - решение затухающего колебания,
- решение затухающего колебания,  - решение незатухающих периодических колебаний с вынуждающей частотой
- решение незатухающих периодических колебаний с вынуждающей частотой 
 (90), где А – амплитуда вынужденных
(90), где А – амплитуда вынужденных  колебаний,
колебаний,  - сдвиг фаз между смещением и вынуждающей силой
- сдвиг фаз между смещением и вынуждающей силой
Установившиеся вынужденные колебания являются так же гармоническими.
Найдем значение амплитуды А и начальной фазы  .
.
Для этого запишем уравнение для скорости и ускорения и подставим их в (88)
 (91)
(91)
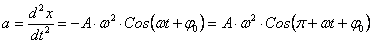 (92)
(92)
 (93)
(93)
Для упрощения решения можно воспользоваться методом векторных диаграмм:
Из рисунка видно, что
 (94)Результирующая амплитуда равна:
(94)Результирующая амплитуда равна:
 (95)
(95)
Из рисунка найдем начальную фазу результирующего колебания  ( сдвиг фаз между смещением и вынуждающей силой):
( сдвиг фаз между смещением и вынуждающей силой):  (96)
(96)
- x(t), v(t), a(t) в случае незатухающих колебаний.
- Кинетическая, потенциальная, полная механическая энергии в случае незатухающих механических колебаний.
Ø кинетическая энергия (  ):
):
В колебаниях любых систем происходит непрерывное превращение кинетической энергии в потенциальную и обратно. Например при колебаниях М.М. и Ф.М.
Кинетическая энергия системы, совершающей гармонические колебания, равна:
 , (43)где скорость изменяется по гармоническому закону:
, (43)где скорость изменяется по гармоническому закону:
 (44)
(44)
После подстановки, имеем:
 (45) Если учесть, что
(45) Если учесть, что 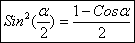 (46)
(46)
и 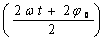 , кинетическая энергия будет равна:
, кинетическая энергия будет равна: 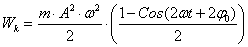 (47) Согласно формулам приведения:
(47) Согласно формулам приведения:  , получим
, получим
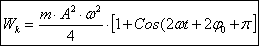 (48) Вывод:
(48) Вывод: 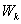 физической системы совершает гармонические колебания с круговой частотой
физической системы совершает гармонические колебания с круговой частотой  , а величина ее периодически изменяется от 0 до
, а величина ее периодически изменяется от 0 до  .
.
Øпотенциальная энергия (  );
);
Любая физическая система совершает гармонические колебания под действием квазиупругой силы, потенциальную энергию можно найти по формуле потенциальной энергии упруго-деформированного тела:
 (49)т.к.
(49)т.к. 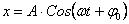 , то подставляя, получаем:
, то подставляя, получаем:
 (50)Т.к.
(50)Т.к. 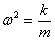 , то
, то  , тогда
, тогда
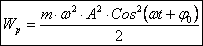 (51) Если учесть, что
(51) Если учесть, что 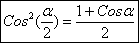 (52)
(52)
и 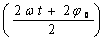 , потенциальная энергия будет равна:
, потенциальная энергия будет равна:
 (53)
(53)  (54) Вывод:
(54) Вывод:  физической системы совершает гармонические колебания с круговой частотой
физической системы совершает гармонические колебания с круговой частотой  , а величина ее периодически изменяется от 0 до
, а величина ее периодически изменяется от 0 до  .
.
Ø полная энергия гармонических колебаний (  );
);
По определению полная механическая энергия системы равна алгебраической сумме кинетической и потенциальной энергий:
 (55)Т.к.
(55)Т.к.  и
и  , то
, то  (56)
(56)  (57)
(57)
Вывод:  механической системы прямо пропорциональна
механической системы прямо пропорциональна  и не зависит от времени.
и не зависит от времени.
- x(t), v(t), a(t) в случае затухающих колебаний.
- Математический маятник. Период, частота, циклическая частота колебательного движения.

|
| Рисунок 2.3.1. Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге |
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести  Уравновешиваетсясилой натяжения нити
Уравновешиваетсясилой натяжения нити  . При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
. При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
Период колебаний  Или
Или  (формула Галилея).Частота колебаний
(формула Галилея).Частота колебаний 
Циклическая частота при колебаниях математического маятника  .
.
Период колебаний математического маятника не зависит от массы тела!
- Маятник на пружине. Период, частота, циклическая частота колебательного движения.
Это груз, прикрепленный к пружине, массой которой можно пренебречь.
Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.
 Цикл. Частота
Цикл. Частота  Ускорение
Ускорение 
- Логарифмический декремент затухания, добротность.
Логарифмический декремент затухания прямо пропорционален произведению коэффициента затухания и периоду затухающих колебаний:
 (81)
(81)
Øдобротность  (безразмерна)
(безразмерна)
Добротность – величина, характеризующая потери энергии при затухающих колебаниях.
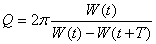 (82)
(82)  или
или  (83)
(83)
- Слабое и сильное затухание.
Слабое затухание.


