 |
Главная |
Исследование функциональных узлов на операционных усилителях
|
из
5.00
|
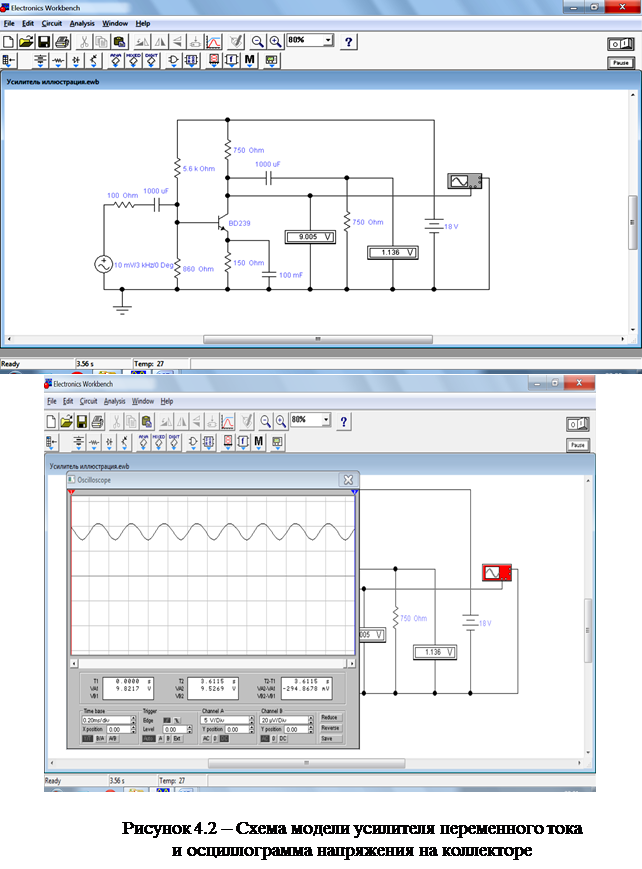
Наиболее часто используемым усилителем в интегральном исполнении является операционный усилитель (ОУ) – усилитель постоянного тока с дифференциальным входом, предназначенный для выполнения операций над аналоговыми величинами.
Чтобы обеспечить возможность работы ОУ как с положительными, так и с отрицательными входными сигналами, требуется двухполярное питающее напряжение.
В большинстве случаев при анализе схем, построенных на ОУ, пользуются понятием "идеальный операционный усилитель". Под этим подразумевается ОУ, обладающий следующими свойствами:
─ бесконечно большой коэффициент усиления дифференциального сигнала;
─ нулевой коэффициент усиления синфазного сигнала;
─ бесконечно большое входное сопротивление;
─ бесконечно малое выходное сопротивление;
─ нулевое напряжение смещения нуля;
─ бесконечно широкая полоса пропускания.
Параметры современных ОУ весьма близки к идеальным. Отличие реальных параметров от идеальных учитывается, если необходимо определить погрешность преобразования сигнала.
При расчете характеристик функциональных узлов на ОУ пользуются так называемым принципом виртуального нуля (его называют также принципом мнимой земли). Суть принципа в том, что разность потенциалов между входами ОУ, находящегося в линейном режиме, принимается равной нулю.
Важнейшей характеристикой линейного функционального звена является его передаточная функция. В настоящей работе передаточную функцию следует выводить в следующем порядке:
1. Изображается схема с указанием операторного сопротивления конденсатора.
2. Составляется уравнение по первому закону Кирхгофа в операторной форме. При этом обязательно следует учитывать три свойства идеального ОУ: бесконечно большое входное сопротивление, бесконечно малое выходное сопротивление и бесконечно большой коэффициент усиления. Следствием этих свойств является принцип "мнимой земли" и отсутствие ответвления тока во входную цепь ОУ. Полученное уравнение выражает связь между входным и выходным напряжениями.
3. Из уравнения выводится выражение для передаточной функции W(p) = Uвых(p)/Uвх(p).
Амплитудно-частотная характеристика (АЧХ) представляет собой зависимость модуля коэффициента передачи схемы от частоты K(ω) = |W(jω)|. Отсюда следует, что в полученной передаточной функции W(р) следует заменить р на jω и взять модуль от полученного комплексного выражения по правилам обращения с комплексными числами.
Задание на подготовку к лабораторной работе:
1. Изучить материал о свойствах операционных усилителях (ОУ), основных схемах их включения, типовых преобразователях сигналов на базе ОУ, методах анализа схем на базе ОУ, используя учебную литературу [1, с. 424 – 475], [3, с. 273 – 314], [2, с. 67 – 77], [2, с. 17 – 27].
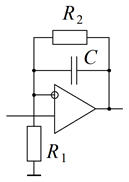
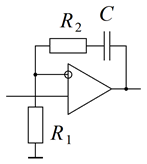
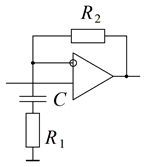
2. Вывести в общем виде передаточную функцию звена на ОУ, указанного в таблице вариантов. Схемы звеньев приведены на рис. 5.
3. Получить выражение для АЧХ звена, подставить параметры элементов из таблицы вариантов, рассчитать и построить график АЧХ.
Задание на выполнение лабораторной работы:
1. Собрать модель звена.
2. Подключить к входу источник синусоидального сигнала. Снять и построить АЧХ звена, сравнить с теоретическим графиком.
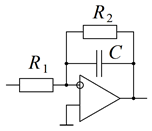 а)
а)
| 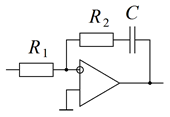 б)
б)
| 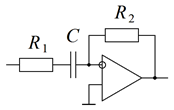 в)
в)
|
 г)
г)
|  д)
д)
|  е)
е)
|
| Рис. 5. Схемы динамических звеньев |
Варианты задания:
| Студент | Схема | R1, кОм | R2, кОм | С, нФ |
| Баразгов Т. С. | а | |||
| Богуш М. В. | б | |||
| Гапеев А. В. | в | |||
| Горбачев М. А. | г | |||
| Горностаев К. А. | д | |||
| Григорович В. А. | е | |||
| Гудовщиков В. Ю. | а | |||
| Дрожжин А. А. | б | |||
| Меньшиков С. Н. | в | |||
| Разуменко И. А. | г | |||
| Сапроненко М. А. | д | |||
| Стуков М. Н. | е | |||
| Сучков Д. Л. | а | |||
| Финогенов И. В. | б | 1,5 |
В отчете должны быть приведены:
1. Задание.
2. Данные своего варианта.
3. Схема звена.
4. Вывод передаточной функции и расчет АЧХ.
5. Расчетный график АЧХ
6. Схема модели в виде скриншота.
7. Таблицы данных, полученных при работе модели.
8. Экспериментальный график АЧХ.
9. Вывод о характере динамического звена.
|
из
5.00
|
Обсуждение в статье: Исследование функциональных узлов на операционных усилителях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

