ЧАСТЬ 4. Я, ДРУГИЕ И «ИНЫЕ» 24 страница

При.южеши* Б

6ЭГ27%

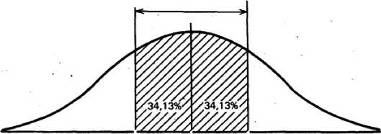
М-0 М М+о

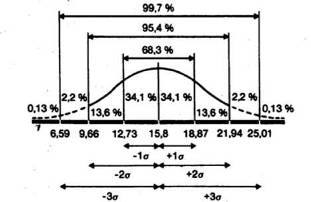
Точно гак же рассчитали, что 94,45% элементов популяции при нормальном распределении не выходит за пределы двух стандартных отклонений от средней:

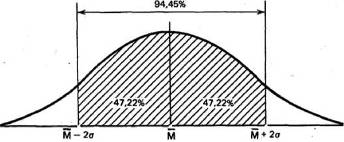
и что в пределах трех стандартных отклонений умещается почти вся популяция-99,73%.

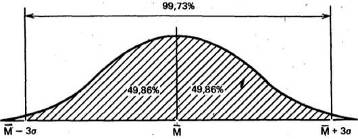
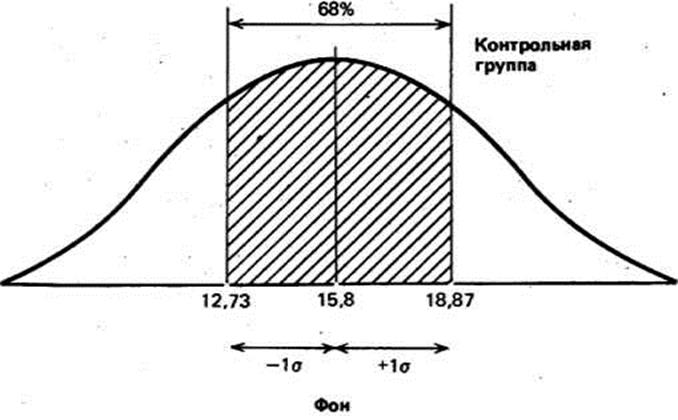
Учитывая, что распределение частот фона контрольной группы довольно близко к нормальному, можно полагать, что 68% членов всец популяции, из которой взята выборка, тоже будет получать сходные результаты, т,е, попадать примерно в 13-19 мишеней из 25, Распределе­ние результатов остальных членов популяции должно выглядеть следу­ющим образом;

Статистики tt обработка данных

Гипотетическая популяция,

из которой взята контрольная группа (фон)

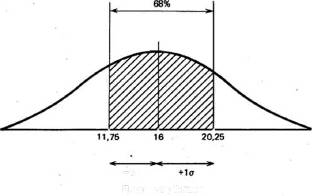
Что касается результатов той же группы после воздействия изучаемо­го фактора, то стандартное отклонение для них оказалось равным 4,25 (пораженных мишеней). Значит, можно предположить, что 68% резуль­татов будут располагаться именно в этом диапазоне отклонений от средней, составляющей 16 мишеней, т. е. в пределах от 11,75 (16 — 4,25) до 20,25 (16 + 4,25), или, округляя, 12 — 20 мишеней из 25. Видно, что здесь разброс результатов больше, чем в фоне. Эту разницу в разбросе между двумя выборками для контрольной группы можно графически представить следующим образом:

Приложение И

-t<7

После воздействия

Поскольку стандартное отклонение всегда соответствует одному и тому же проценту результатов, укладывающихся в его пределах вокруг средней, можно утверждать, что при любой форме кривой нормального распределения та доля ее площади, которая ограничена (с обеих сторон) стандартным отклонением, всегда одинакова и соответствует одной и той же доле всей популяции. Это можно проверить на тех наших выборках, для которых распределение близко к нормальному,-на дан­ных о фоне для контрольной и опытной групп.

Итак, ознакомившись с описательной статистикой, мы узнали» как можно представить графически и оценить количественно степень разбро­са данных в том или ином распределении. Тем самым мы смогли понять, чем различаются в нашем опыте распределения для контрольной группы до и после воздействия. Однако можно ли о чем-то судить по этой разнице-отражает ли она действительность или же это просто артефакт, связанный со слишком малым объемом выборки? Тот же вопрос (только еще острее) встает и в отношении экспериментальной группы, подверг­нутой воздействию независимой переменной. В этой группе стандартное отклонение для фона и после воздействия тоже различается примерно на 1 (3,14 и 4,04 соответственно). Однако здесь особенно велика разница между средними-15,2 и 11,3* На основании чего можно было бы утверждать, что эта разность средних действительно достоверна, т,е\ достаточно велика, чтобы можно было с уверенностью объяснить ее влиянием независимой переменной, а не простой случайностью? В какой степени можно опираться на эти результаты и распространять их на всю популяцию, из которой взята выборка, т, е. утверждать, что потребление марихуаны и в самом деле обычно ведет к нарушению глазодвигатель­ной координации? -

На все эти вопросы и пытается дать ответ индуктивная статистика.

u u oopitwowKu (кишы.\

Индуктивная статистика

Задачи индуктивной статистики заключаются в том, чтобы опреде­лять, насколько вероятно, что две выборки принадлежат к одной популяции.

Давайте наложим друг на друга,, с одной стороны, две кривые-до и после воздействия-для контрольной группы и> с другой стороны, две аналогичные кривые для опытной группы. При этом масштаб кривых должен быть одинаковым.

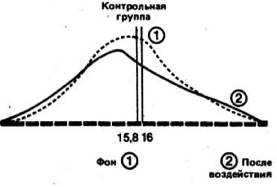
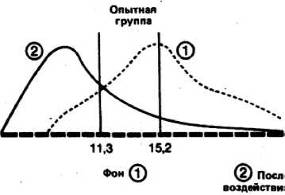
Видно, что в контрольной группе разница между средними обоих распределений невелика, и поэтому можно думать, что обе выборки принадлежат к одной и той же популяции. Напротив, в опытной группе большая разность между средними позволяет предположить что рас­пределения для фона и воздействия относятся к двум различным популяциям, разница между которыми обусловлена тем, что на одну из них повлияла независимая переменная.

Проверка гипотез

Как уже говорилось, задача индуктивной статистики - определять достаточно ли велика разность между средними двух распределений для того, чтобы можно было объяснить ее действием независимой перемен­ной, а не случайностью, связанной с малым объемом выборки (как,

2%

по-видимому, обстоит дело в случае с опытной группой нашего экспе­римента).

При этом возможны две гипотезы:

1) нулевая гипотеза (Но), согласна которой разница между распреде­лениями недостоверна; предполагается, что различие недостаточно зна­чительно, и поэтому распределения относятся к одной и той же популя­ции, а независимая переменная не оказывает никакого влияния;

2) альтернативная гипотеза (НД какой является рабочая гипотеза нашего исследования. В соответствии с этой гипотезой различия между обоими распределениями достаточно значимы и обусловлены влиянием независимой переменной.

Основной принцип метода проверки гипотез состоит в том, что выдвигается нулевая гипотеза Но, с тем чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу Нх, Действитель­но, если результаты статистического теста, используемого для анализа разницы между средними, окажутся таковы, что позволят отбросить Но, это будет означать, что верна HL, т.е. выдвинутая рабочая гипотеза по дт ве рж дается.

В гуманитарных науках принято считать, что нулевую гипотезу можно отвергнуть в пользу альтернативной гипотезы, если по результа­там статистического теста'вероятность случайного возникновения най­денного различия не превышает 5 из 100!. Если же этот уровень достоверности не достигается, считают, что разница вполне может быть случайной и поэтому нельзя отбросить нулевую гипотезу.

Для того чтобы судить о том, какова вероятность ошибиться, принимая или отвергая нулевую гипотезу, применяют статистические методы, соответствующие особенностям выборки.

Так, для количественных данных (см. дополнение БЛ) при распреде­лениях, близких к нормальным, используют параметрические методы, основанные на таких показателях, как средняя и стандартное отклоне­ние. В частности, для определения достоверности разницы средних для двух выборок применяют метод Стьюдента, а для того чтобы судить о различиях между тремя или большим числом выборок,-тест F, или дисперсионный анализ.

Если же мы имеем дело с неколичественными данными или выборки слишком малы для уверенности в том, что популяции, из которых они взяты, подчиняются нормальному распределению, тогда используют непараметрические методы -критерий х2 (лм-квадрат) для качественных данных и критерии знаков, рангов, Манна-Уитни, Вилкоксона и др, для порядковых данных.

Кроме того, выбор статистического метода зависит от того, явля­ются ли те выборки, средние которых сравниваются, независимыми (т. е,, например, взятыми из двух разных групп испытуемых) кли зависимыми

\ Разумеется, рнск ошибиться будет еще меньше, если окажется, что эта вероятность составляет 1 на 100 или* еще лучше, I на 1000.

Статистика и оорашгпжи данных

(т. е. отражающими результаты одной и той же группы испытуемых до и после воздействия или после двух различных воздействий).

Дополнение Б.З. Уровни достоверности (значимости)

Тот или иной вывод с некоторой вероятностью может оказаться ошибочным, причем эта вероятность тем меньше, чем больше имеется данных для обоснования этого вывода. Таким образом, чем больше получено результатов, тем в большей степени по различиям между двумя выборками можно судить о том, что действительно имеет место в той популяции, из которой взяты эти выборки.

Однако обычно используемые выборки относительно невелики, и в этих случаях вероятность ошибки может быть значительной, В гумани­тарных науках принято считать, что разница между двумя выборками отражает действительную разницу между соответствующими популя­циями лишь в том случае, если вероятность ошибки для этого утвержде­ния не превышает 5%, т.е. имеется лишь 5 шансов из 100 ошибиться, выдвигая такое утверждение. Это так называемый уровень достоверно­сти (уровень надежности, доверительный уровень) различия. Если этот уровень не превышен, то можно считать вероятным, что выявленная нами разница действительно отражает положение дел в популяции (отсюда еще одно название этого критерия-порог вероятности).

Для каждого статистического метода этот уровень можно узнать из таблиц распределения критических значений соответствующих крите­риев (f, х1 и т, д.); в этих таблицах приведены цифры для уровней 5% (0,05), 1% (0,01) или еще более высоких. Если значение критерия для данного числа- степеней свободы (см. дополнение Б.4) оказывается ниже критического уровня, соответствующего порогу вероятности 5%, то нулевая гипотеза не может считаться опровергнутой, и это означает, что выявленная разница недостоверна.

Параметрические методы

Метод Стьюдента (tf-тест)

Это параметрический метод, используемый для проверки гипотез о достоверности разницы средних при анализе количественных данных о популяциях с нормальным распределением и с одинаковой вариан-сой *.

Метод Стьюдента различен для независимых и зависимых выборок. Независимые выборки получаются при исследоваиии двух различных

1 К сожалению, метод Стьюдента слишком часто используют для малых выборок, не убедившись предварительно в том, что данные в соответствующих популяциях подчиняются закону нормального распределения (например, ре­зультаты выполнения слишком легкого задания, с которым справились все испытуемые* или же, наоборот, слишком трудного задания не дают нормального распределения).

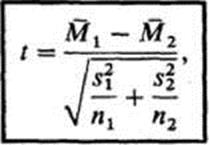
групп испытуемых (в нашем эксперименте это контрольная и опытная группы). В случае независимых выборок для анализа разницы средних применяют формулу

где 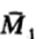-средняя первой выборки; 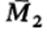-средняя второй выборки;

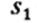-стандартное отклонение

для первой выборки; 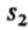-стандартное отклонение

для второй выборки; 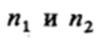-число элементов в первой

и второй выборках.

Теперь осталось лишь найти в таблице значений t (см. дополнение Б.5) величину, соответствующую п — 2 степеням свободы, где л-общее число испытуемых в обеих выборках (см. дополнение Б,4), и сравнить эту величину с результатом расчета по формуле.

Если наш результат больше, чем значение для уровня достоверности 0,05 (вероятность 5%), найденное в таблице* то можно отбросить нулевую гипотезу (Но) и принять альтернативную гипотезу (НД т,е, считать разницу средних достоверной.

Если же, напротив, полученный при вычислении результат меньше, чем табличный (для п-2 степеней свободы), то нулевую гипотезу нельзя отбросить и, следовательно, разница средних недостоверна,

В нашем эксперименте с помощью метода Стьюдента для независи­мых выборок можно было бы, например, проверить, существует ли достоверная разница между фоновыми уровнями (значениями, получен­ными до воздействия независимой переменной) для двух групп. При этом мы получим:

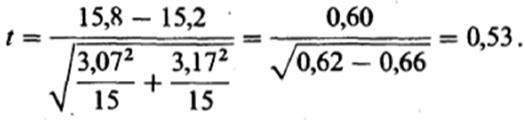
Сверившись с таблицей значений /, мы можем прийти к следующим выводам; полученное нами значение / — 0,53 меньше того, которое соответствует уровню достоверности 0,05 для 26 степеней свободы I 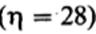; следовательно, уровень вероятности для такого / будет выше

0,05 и нулевую гипотезу нельзя отбросить; таким образом, разница между двумя выборками недостоверна, т. е. они вполне могут принадле­жать к'одной популяции.

Сокращенно этот вывод записывается следующим образом:

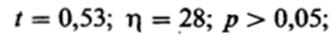недостоверно.

 

Однако наиболее полезным f-тест окажется для нас при проверке

1 Как уже говорилось, поскольку объем выборок в данном случае невелик, а результаты опытной группы после воздействия не соответствуют нормальному распределению, лучше использовать непараметрический метод, например U-тест Манна -Уитни.

Спитш-тика и мраоотка омнных

гипотезы о достоверности разницы средней между результатами опыт­ной и контрольной групп после воздействия1. Попробуйте сами найти для этих выборок значения и сделать соответствующие выводы:

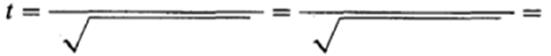
Значение t ....., чем табличное для 0,05 (.....степеней свободы).

Следовательно, ему соответствует порог вероятности ___•, чем 0,05,

В связи с этим нулевая гипотеза может (не может) быть отвергнута. Разница между выборками достоверная (недостоверна?):

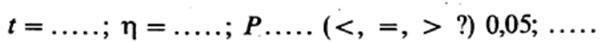
Дополнение Б.4. Степени свободы

Для того чтобы свести к минимуму ошибки, в таблицах критических значений статистических критериев в общем количестве данных не учитывают те, которые можно вывести методом дедукций. Оставшиеся данные составляет так называемое число степеней свободы* т. е. то число данных из выборки, значения которых могут быть случайными.

Так, если сумма трех данных равна 8, то первые два из них могут принимать любые значения, но если они определены, то третье значение становится автоматически известным. Если, например, значение первого данного равно 3>а второго-1, то третье может быть равным только 4. Таким образом, в такой выборке имеются только две степени свободы. В общем случае для выборки в п данных существует п-1 степень свободы.

Если у нас имеются две независимые выборки, то число степеней свободы для первой из них составляет пг-\, а для второй-л2-Ь А поскольку при определении достоверности разницы между ними опираются на анализ каждой выборки, число степеней свободы, по которому нужно будет находить критерий г в таблице, будет составлять К + «а) - 2. " .

Если же речь идет о двух зависимых выборках, то в основе расчета лежит вычисление суммы разностей, полученных для каждой, пары результатов (т.е., например, разностей между результатами до и после воздействия на одного и того же испытуемого). Поскольку одну (любую) из этих разностей можно вычислить» зная остальные разности и их сумму, число степеней свободы для определения- критерия г будет равно и- 1.

Метод Стьюдента для зависимых выборок

К зависимым выборкам относятся» например, результаты одной и той же группы испытуемых до и после воздействия независимой переменной. В нашем случае с помощью статистических методов для зависимых выборок можно проверить гипотезу о достоверности разни-

300 Пщмож*-нш* В

цы между фоновым уровнем и уровнем после воздействия отдельно для опытной и для контрольной группы.

Для определения достоверности разницы средних в случае зависимых выборок применяется следующая формула:

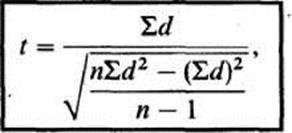
где 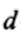-разность между результатами

в каждой паре;

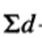-сумма этих частных разностей; 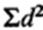-сумма квадратов частных разностей.

Полученные результаты сверяют с таблицей и отыскивая в ней значения, соответствующие « — 1 степени свободы; «-это в данном случае число пар данных (см. дополнение Б.З).

Перед тем как использовать формулу, необходимо вычислить для каждой группы частные разности между результатами во всех парах, квадрат каждой из этих разностей, сумму этих разностей и сумму их квадратов1.

Необходимо произвести следующие операции:

Контрольная группа. Сравнение результатов для фонд н после

воздействия

Испытуемые	Фок	После uov	d
		дейстзия
Д 1			+ 2
	ю-	S	-2
г			+ 1
			-2
			+3
			-2
			— 2
Ю 1		J7	+2
			+ 1
				_
			+ 1
	15 .		+ 1
			-3
			_	—
			+ 3

1 Все эти расчеты необходимо сделать в чисто учебных целях. Сегодня существуют более быстрые методы, при которых основная работа сводятся к вводу данных в программируемый микрокалькулятор или в компьютер, который автоматически выдает результат. Приведенная здесь таблица помогает понять все расчеты, которые осуществляются такими машинами.

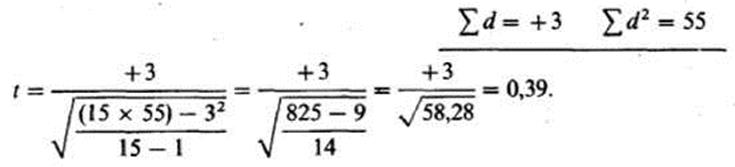
и ищпюотки данных 301

Величина / = 0,39 ниже той, которая необходима для уровня значимости 0,05 при 14 степенях свободы. Иными словами, порог вероятности для такого / выше 0,05. Таким образом, нулевая гипотеза не может быть отвергнута, и разница между выборками недостоверна. В сокращенном

виде это записывается следующим образом:

'л

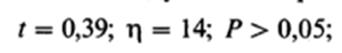недостоверно.

Теперь попробуйте самостоятельно применить метод Стьюдента для зависимых выборок к обоим распределениям опытной группы с учетом того, что вычисление частных разностей для дар дало следующие результаты: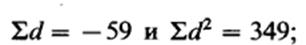

 

Значение t....., чем то, которое соответствует уровню значимости G>05

для.....степеней свободы. Значит, нулевая гипотеза....., а различи»

между выборками.....

Запишите это в сокращенном виде.

 

Дисперсионный анализ (тест F Снедекора)

Метод Снедекора-это параметрический тест, используемый в тех случаях, когда имеются три или большее число выборок. Сущность этого метода заключается в том, чтобы определить, является ли разброс средних для различных выборок относительно общей средней для всей совокупности данных достоверно отличным от разброса данных относи­тельно средней в пределах каждой выборки. Если все выборки принадле­жат одной и той же популяции, то разброс между ними должен быть не больше, чем разброс данных внутри их самих.

В методе Снедекора в качестве показателя разброса используют вариансу (дисперсию). Поэтому анализ сводится к тому, чтобы сравнить вариансу распределений между выборками с вариансами в пределах каждой выборки, или:

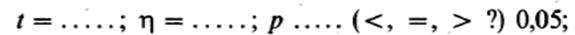различие .....

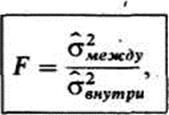
где 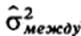-варианса средних каждой выборки относительно общей

средней:

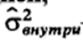-варианса данных внутри каждой выборки. Если различие между выборками недостоверно, то результат должен быть близок к 1, Чем больше будет F по сравнению с 1, тем более достоверно различие.

ft pit. r* мнение

Таким образом, дисперсионный анализ показывает, принадлежат ли выборки к одной популяции, но с его помощью нельзя выделить те выборки, которые отличаются от других. Для того чтобы определить те пары выборок, разница между которыми достоверна, следует после дисперсионного анализа применить метод Шеффе* Поскольку, однако, этот весьма ценный метод требует достаточно больших вычислений, а к нашему гипотетическому эксперименту он неприменим, мы рекомен­дуем читателю для ознакомления с ним обратиться к какому-либо специальному пособию по статистике.

-

Непараметрические методы

Метод %2 («хи-квадрат»)

Для использования непараметрического метода х2 не требуется вычислять среднюю или стандартное отклонение. Его преимущество состоят в том, что для применения его необходимо знать лишь зависи­мость распределения частот результатов от двух переменных; это позволяет выяснить, связйы они друг с другом или, наоборот, независи­мы. Таким образом, этот статистический метод используется для обра­ботки качественных данных (см. дополнение БЛ)+ Кроме того, с его помощью можно проверить, существует ли достоверное различие между числом людей, справляющихся или нет с заданиями какого-то интеллек­туального теста, и числом этих же людей, получающих при обучении высокие или низкие оценки; между числом больных, получивших новое лекарство, и числом тех, кому это лекарство помогло; и, наконец, существует ли достоверная связь между возрастом людей и их успехом или неудачей в выполнении тестов на память и т. п. Во всех подобных случаях этот тест позволяет определить число испытуемых, удовлетво­ряющих одному и тому же критерию для каждой из переменных,

При обработке данных нашего гипотетического эксперимента с по­мощью метода Стьюдента мы убедились в том, что употребление марихуаны испытуемыми из опытной группы снизило у них эффектив­ность выполнения задания по сравнению с контрольной группой. Одна­ко к такому же выводу можно быдо бы прийти с помощью другого метода -х2- Для этого метода нет ограничений, свойственных методу Стьюдента: он может применяться н в тех случаях, когда распределение не является нормальным, а выборки невелики.

При использовании метода х2 достаточно сравнить число испытуе­мых в ТОЙ и другой группе, у которых снизилась результативность, и подсчитать, сколько среди них было получивших и не получивших наркотик; после этого проверяют, есть ли связь между этими двумя переменными.

Из результатов нашего опыта, приведенных в таблице в дополнении Б,2, видно, что из 30 испытуемых, составляющих опытную и контроль­ную группы, у 18 результативность снизилась, а 13 из них получили марихуану. Теперь надо внести значение этих так называемых эмпириче­ских частот (Э) в специальную таблицу:

и oopainrnwa *>шшы.\

			Результаты
	Ухудшение Без изменений или улучшение	Итого • -
ос	После употреб­ления наркотика
О О	Без наркотика
	Итого

г

Эмпирические частоты (Э)

Далее надо сравнить эти данные с теоретическими частотами (Т), которые были бы получены, если бы все различия были чисто случайны­ми. Если учитывать только итоговые данные, согласно которым, с од­ной стороны, у 18 испытуемых результативность снизилась, а у 12-по­высилась, а с другой-15 из всех испытуемых курили марихуану, а 15-нет, то теоретические частоты будут следующими:

Результаты

Ухудшение Без изменений Итого

или улучшение

 

 

 

 

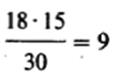
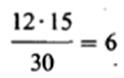
После употреб-				1 с
в лен и я на кортика		1 э
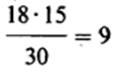
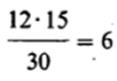
5 Без наркотика				1С
Итого

Теоретические частоты (Т)

Метод х2 состоит в том, что оценивают, насколько сходны между собой распределения эмпирических и теоретических частот. Если разни­ца между ними невелика, то можно полагать, что отклонения эмпириче­ских частот от теоретических обусловлены случайностью. Если же, напротив, эти распределения будут достаточно разными, можно будет считать, что различия между ними значимы и существует связь между действием независимой переменной и распределением эмпирических частот*

Для вычисления 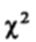определяют разницу между каждой эмпирической

304 fIpu.w.iKvrt!ti' Fi

и соответствующей теоретической частотой по формуле

 

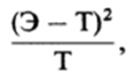
а затем результаты, полученные по всех таких сравнениях, складывают:

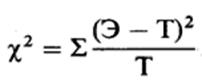
В нашем случае все это можно представить следующим образом:

Наркотик, ухудшение			+4		1,77 -
Наркотик, улучшение			-4 -		2,66
Без наркотика, ухудшение			_4		1,77
Без наркотика, улучшение			+4		2,66

Для расчета числа степеней свободы число строк в табл. 2 (в конце приложения Б) за вычетом единицы умножают на число столбцов за вычетом единицы. Таким образом, в нашем случае число степеней свободы равно (2 — 1)* (2 — 1) = 1,

Табличное значение 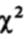(см, табл, 2 в дополнении Б.5) для уровня значимости 0,05 и 1 степени свободы составляет 3,84, Поскольку вычис­ленное нами значение 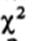намного больше, нулевую гипотезу можно считать опровергнутой. Значит, мевду употреблением наркотика и гла­зодвигательной координацией действительно существует связь1.

Критерий знаков (биномиальный критерий)

Критерий знаков-это еще один непараметрический метод, позволя­ющий легко проверить, повлияла ли независимая переменная на выпол-

1 Следует, однако, отметить* что если число степеней свободы больше 1, то критерий 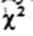нельзя применять, когда в 20 или более процентах случаев теоре­тические частоты меньше 5 или когда хотя бы в одном случае теоретическая частота равна 0 (Siegel, 1956).

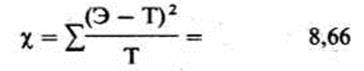
if и ooptwonma йштых%

нение задания испытуемыми. При этом методе сначала подсчитывают

число испытуемых, у которых результаты снизились, а затем сравни­вают его с тем числом, которого можно было ожидать на основе чистой случайности (в нашем случае вероятность случайного события 1:2). Далее определяют разницу между этими двумя числами, чтобы выяс­нить, насколько она достоверна.