 |
Главная |
Классификация колебательных процессов
|
из
5.00
|
Свободные колебания.
Вынужденные колебания.
Параметрические колебания.
Автоколебания (самовозбуждающиеся колебания).

 Свободные колебания. Свободные колебания совершаются при отсутствии переменного внешнего воздействия, без притока энергии извне. Такие колебания могут происходить лишь в автономных системах (рис. 1).
Свободные колебания. Свободные колебания совершаются при отсутствии переменного внешнего воздействия, без притока энергии извне. Такие колебания могут происходить лишь в автономных системах (рис. 1).
Вынужденные колебания. Такие колебания имеют место в неавтономных системах, и их источниками являются переменные внешние воздействия (рис. 2).
 Параметрические колебания. Параметры колебательной системы могут изменяться во времени, и это может стать источником колебаний. Такие колебания называются параметрическими. Верхняя точка подвеса физического маятника (рис. 3) совершает колебания в вертикальном направлении
Параметрические колебания. Параметры колебательной системы могут изменяться во времени, и это может стать источником колебаний. Такие колебания называются параметрическими. Верхняя точка подвеса физического маятника (рис. 3) совершает колебания в вертикальном направлении  , вследствие чего маятник совершает параметрические колебания вокруг шарнира. На вертикальный стержень в продольном направлении действует периодическая сила P(t), вызывая поперечные колебания стержня (рис. 4). Правая опора балки колеблется в горизонтальном направлении по закону
, вследствие чего маятник совершает параметрические колебания вокруг шарнира. На вертикальный стержень в продольном направлении действует периодическая сила P(t), вызывая поперечные колебания стержня (рис. 4). Правая опора балки колеблется в горизонтальном направлении по закону  , что служит причиной возникновения поперечных параметрических колебаний (рис. 5).
, что служит причиной возникновения поперечных параметрических колебаний (рис. 5).
 Автоколебания (самовозбуждающиеся колебания). У таких колебаний источники имеют неколебательную природу, и при этом сами источники включены в колебательную систему. На рис. 6 показана масса на пружине, лежащая на движущейся ленте. На неё действуют две силы: сила трения и упругая сила натяжения пружины, и они меняются во времени. Первая зависит от разности скоростей ленты и массы, вторая от величины и знака деформации пружины, поэтому масса находится под воздействием равнодействующей силы, направленной то влево, то вправо и совершает колебания.Во втором примере (рис. 7) левый конец пружины перемещается вправо с постоянной скоростью v, вследствие чего пружина перемещает груз по неподвижной поверхности. Образуется ситуация, подобная описанной для предыдущего случая, и груз начинает колебаться.
Автоколебания (самовозбуждающиеся колебания). У таких колебаний источники имеют неколебательную природу, и при этом сами источники включены в колебательную систему. На рис. 6 показана масса на пружине, лежащая на движущейся ленте. На неё действуют две силы: сила трения и упругая сила натяжения пружины, и они меняются во времени. Первая зависит от разности скоростей ленты и массы, вторая от величины и знака деформации пружины, поэтому масса находится под воздействием равнодействующей силы, направленной то влево, то вправо и совершает колебания.Во втором примере (рис. 7) левый конец пружины перемещается вправо с постоянной скоростью v, вследствие чего пружина перемещает груз по неподвижной поверхности. Образуется ситуация, подобная описанной для предыдущего случая, и груз начинает колебаться.
2. http://vunivere.ru/work45156?screenshots=1
Основными характеристиками механических колебаний являются амплитуда, период, частота и фаза колебаний.
Амплитуда – это модуль максимального отклонения тела от положения равновесия.
Период – это время одного полного колебания. (Т, секунды)
Частота – число полных колебаний, совершаемых за единицу времени.(ν, Герцы)
Период и частота связаны формулой: 
Простейший вид колебательного движения – гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Уравнение гармонических колебаний:  , где
, где  амплитуда,
амплитуда, 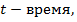
 . Величина, стоящая под знаком косинуса (угол), называется фазой. Фаза равна:
. Величина, стоящая под знаком косинуса (угол), называется фазой. Фаза равна:  .
.
3. Зависимость амплитуды и начальной фазы колебаний от начальных условий.
Решения дифференциального уравнения колебаний определены с точностью до постоянной величины, поэтому таких решений бесчисленное множество. Выбор решения для данной конкретной колебательной системы можно сделать, если задать ее поведение в начальный момент времени, то есть начальные условия. Например, если просто отклонить маятник, растянув пружину, а затем спокойно отпустить его, или отклонить, а затем подтолкнуть маятник, то движения маятника будут различными. Рассмотрим зависимость параметров колебательной системы от начальных условий.
Пусть при t = 0 смещение системы от положения равновесия равно х0, а начальная скорость v0. Гармоническое колебание описывается уравнением  . При t = 0 имеем два уравнения:
. При t = 0 имеем два уравнения: 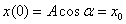 ,
,  .
.
Возведя в квадрат оба уравнения и сложив их, получим уравнение для амплитуды:
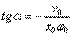

Поделив одно уравнение на другое, получим соотношение для начальной фазы:
.
Таким образом, и амплитуда, и начальная фаза колебаний зависят от начальных условий колебательной системы.
4.
Линейным одномерным гармоническим осциллятором называют частицу массы  , совершающую одномерное движение под действием квазиупругой силы , совершающую одномерное движение под действием квазиупругой силы 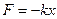 .
Уравнение движения
. .
Уравнение движения
.
 Собственная частота классического гармонического осциллятора Собственная частота классического гармонического осциллятора
 , откуда , откуда  .
Потенциальная энергия осциллятора
. .
Потенциальная энергия осциллятора
.
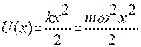 Рассмотрение колебательной системы методами квантовой механики: уравнение Шредингера для стационарных состояний частицы в параболической потенциальной яме Рассмотрение колебательной системы методами квантовой механики: уравнение Шредингера для стационарных состояний частицы в параболической потенциальной яме
 . Преобразуем это уравнение следующим образом . Преобразуем это уравнение следующим образом
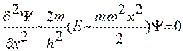 ; ;  .
Введем обозначения: .
Введем обозначения:  и и  .
Тогда .
Тогда  .
Решение этого уравнения должно удовлетворять следующим требованиям:
1)
.
Решение этого уравнения должно удовлетворять следующим требованиям:
1)  симметрична относительно начала координат, следовательно, симметрична относительно начала координат, следовательно,  должно быть тоже симметрична по отношению к началу координат ( должно быть тоже симметрична по отношению к началу координат (  - симметрична или асимметрично);
2) при - симметрична или асимметрично);
2) при   .
Предположим, что .
Предположим, что  - решение уравнения Шредингнра.
Тогда - решение уравнения Шредингнра.
Тогда
 и и  .
Подставляя решение в уравнение Шредингера, получим .
Подставляя решение в уравнение Шредингера, получим  или
или
 .
Отсюда следует, что искомая функция будет решением при .
Отсюда следует, что искомая функция будет решением при  . Тогда . Тогда  .
Следовательно,
.
Следовательно,  . Состояние с энергией . Состояние с энергией  - основное квантовое состояние осциллятора.
Возможные значения полной энергии гармонического осциллятора - основное квантовое состояние осциллятора.
Возможные значения полной энергии гармонического осциллятора
 или или  , ,  .
Энергетический спектр квантового гармонического осциллятора является дискретным, а уровни энергии .
Энергетический спектр квантового гармонического осциллятора является дискретным, а уровни энергии  - эквидистантны - эквидистантны  .
Взаимодействие квантового осциллятора с фотоном (излучение или поглощение света) приводит к изменению вида функции: превращает симметричную функцию в антисимметричную, и наоборот. Это приводит к необходимости правила отбора .
Взаимодействие квантового осциллятора с фотоном (излучение или поглощение света) приводит к изменению вида функции: превращает симметричную функцию в антисимметричную, и наоборот. Это приводит к необходимости правила отбора  . Поэтому квантово-механический осциллятор способен поглотить лишь . Поэтому квантово-механический осциллятор способен поглотить лишь  и осуществить при этом переход только на соседний уровень.
Из условия нормировки и осуществить при этом переход только на соседний уровень.
Из условия нормировки
 , тогда , тогда  . Т.к. функция симметрична относительно начала координат, то . Т.к. функция симметрична относительно начала координат, то
 . Откуда . Откуда  или или 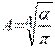 . Таким образом . Таким образом  .
Если известен вид функции .
Если известен вид функции  , то можно найти все другие величины. Среднее значение координаты: , то можно найти все другие величины. Среднее значение координаты:
 . Среднее значение проекции импульса . Среднее значение проекции импульса  .
.
 . .  В квазиклассическом приближении
В квазиклассическом приближении
 .
Отсюда следует, что средние значения потенциальной и кинетической энергий осциллятора равны: .
Отсюда следует, что средние значения потенциальной и кинетической энергий осциллятора равны:
 ; ; 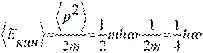 .
Значениям энергии .
Значениям энергии  соответствуют собственные функции соответствуют собственные функции 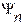 . Все функции . Все функции  должны быть симметричны относительно начала координат Функции должны быть симметричны относительно начала координат Функции  - либо симметричны, либо антисимметричны. При - либо симметричны, либо антисимметричны. При   . Если все эти функции стремятся к нулю на бесконечности, то они должны содержать множитель . Если все эти функции стремятся к нулю на бесконечности, то они должны содержать множитель 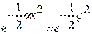 ( (  ). Решение уравнения Шредингера для произвольных ). Решение уравнения Шредингера для произвольных  имеет вид: имеет вид:
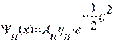 , где , где  - это полином Чебышева-Эрмита, степень которого возрастает с увеличением - это полином Чебышева-Эрмита, степень которого возрастает с увеличением  ; ;  - это нормировочный множитель - это нормировочный множитель
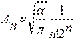 . Следовательно, . Следовательно, 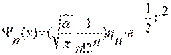 .
Конкретный вид полиномов: .
Конкретный вид полиномов: 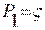 ; ;  ; ;  и т.д.
Некоторые особенности классических и квантовых осцилляторов. 1. Разрешенные значения и т.д.
Некоторые особенности классических и квантовых осцилляторов. 1. Разрешенные значения  для квантово-механического осциллятора представляют собой набор эквидиситантных энергетических уровней, а собственные для квантово-механического осциллятора представляют собой набор эквидиситантных энергетических уровней, а собственные  - функции – набор стоячих волн, заключенных в потенциальной яме параболической формы.
Для классического осциллятора границы этой ямы определяют границы пространства, в котором может быть локализована частица. Расстояние по оси - функции – набор стоячих волн, заключенных в потенциальной яме параболической формы.
Для классического осциллятора границы этой ямы определяют границы пространства, в котором может быть локализована частица. Расстояние по оси  от от  до до  . График . График 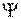 - функции, являющейся решением уравнения Шредингера, выходит за рамки ограничивающей кривой - функции, являющейся решением уравнения Шредингера, выходит за рамки ограничивающей кривой  . Такое поведение . Такое поведение  - функции связано с тем, что она должна быть непрерывной и гладкой везде, в том числе и в точках поворота, и при этом должно выполняться соотношение неопределенности.
2. Вероятность локализации классического осциллятора в окрестностях точки с координатой - функции связано с тем, что она должна быть непрерывной и гладкой везде, в том числе и в точках поворота, и при этом должно выполняться соотношение неопределенности.
2. Вероятность локализации классического осциллятора в окрестностях точки с координатой  в потенциальной яме является наибольшей в точках поворота (где скорость в потенциальной яме является наибольшей в точках поворота (где скорость 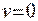 ), т.е. на стенках параболы.
Для квантово-механического осциллятора ), т.е. на стенках параболы.
Для квантово-механического осциллятора  имеет конечное значение и на границах ямы и на некотором расстоянии от нее. Следовательно, существует конечная вероятность локализации частицы вне пределов ямы. Наибольшая вероятность локализации частицы - в точках, соответствующих «пучностям» имеет конечное значение и на границах ямы и на некотором расстоянии от нее. Следовательно, существует конечная вероятность локализации частицы вне пределов ямы. Наибольшая вероятность локализации частицы - в точках, соответствующих «пучностям»  - функций. Для больших - функций. Для больших  функция функция  имеет распределение, близкое к классическому. В этом проявляется принцип соответствия.Начало формы имеет распределение, близкое к классическому. В этом проявляется принцип соответствия.Начало формы
|
5. Колеблющееся тело (осциллятор) обладает кинетической энергией  и потенциальной Wпот.
и потенциальной Wпот.
Поскольку х = Аcos(ω0t), то  ,
, 
Потенциальная энергия зависит от смещения х и равна 
 Подставляя х = Аcos(ω0t) и k = ω02m, имеем
Подставляя х = Аcos(ω0t) и k = ω02m, имеем 
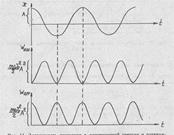
Зависимости Wкин(t)и Wпот(t) показаны на рис. 11.
Полная энергия осциллятора равна
 (2) Рис. 11. Зависимость смещения х, кинетической энергии и
(2) Рис. 11. Зависимость смещения х, кинетической энергии и
потенциальной энергии от времени t.
Итак: полная энергия гармонического осциллятора пропорциональна его массе, квадрату собственной частоты и квадрату амплитуды.
Заменив ω02 = k/m, получаем, что полная энергия пропорциональна коэффициенту упругости и квадрату амплитуды (2).
|
из
5.00
|
Обсуждение в статье: Классификация колебательных процессов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

