 |
Главная |
Приближенных аргументов
|
из
5.00
|
Измерения делят на прямые и косвенные. В первом случае непосредственно измеряется определяемая величина, при косвенных измерениях она задается некоторой функцией от непосредственно измеряемых величин. Подавляющее большинство параметров процессов определяются в результате косвенных измерений, погрешность которых зависит от погрешностей непосредственно измеряемых величин, использованных в расчетах.
Предположим, что некоторые величины 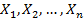 измерены с абсолютными погрешностями
измерены с абсолютными погрешностями  и что измеренные значения используются для вычисления функции
и что измеренные значения используются для вычисления функции

Очевидно, что погрешности приближенных аргументов должны привести к погрешности в значении искомой функции, что можно записать в следующем виде:

где  — абсолютная погрешность функции Z.
— абсолютная погрешность функции Z.
Разложим правую часть равенства (1.15) в ряд Тейлора:

 (1.16)
(1.16)
Если предположить, что измерения достаточно точны, так что величины  малы по сравнению со значениями аргументов
малы по сравнению со значениями аргументов  , то в выражении (1.16) можно отбросить все члены, содержащие абсолютные погрешности аргументов во второй и высшей степенях. Тогда
, то в выражении (1.16) можно отбросить все члены, содержащие абсолютные погрешности аргументов во второй и высшей степенях. Тогда
 (1.17)
(1.17)
откуда с учетом (1.14) получаем
 (1.18)
(1.18)
Выражение для предельной абсолютной погрешности функции n переменных запишется в следующем виде:

т.е. предельная абсолютная погрешность функции независимых переменных равна сумме частных производных этой функции, умноженных на соответствующие абсолютные погрешности аргументов. В практических расчетах значения частных производных берутся в точках, соответствующих измеренным значениям  или средним арифметическим
или средним арифметическим  , если проводились серии измерений. В математической статистике также доказывается, что если абсолютные погрешности аргументов независимы и случайны, то наилучшей оценкой погрешности функции будет квадратичная сумма
, если проводились серии измерений. В математической статистике также доказывается, что если абсолютные погрешности аргументов независимы и случайны, то наилучшей оценкой погрешности функции будет квадратичная сумма
ее частных производных, умноженных на соответствующие погрешности аргументов:
 (1.20)
(1.20)
Формулы (1.19) и (1.20) являются основными при практических расчетах. Из них можно вывести формулы для расчетов погрешностей косвенных измерений для некоторых частных случаев, использование которых на практике бывает более удобным:
1. Измеренная величина умножается на точное число. Если величина X измерена с погрешностью 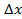 и используется для вычисления
и используется для вычисления

в котором 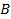 — точное число, то абсолютная погрешность в Z равна
— точное число, то абсолютная погрешность в Z равна

2. Погрешность в суммах и разностях. Если величины 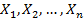 измерены с малыми погрешностями
измерены с малыми погрешностями  и измеренные значения используются для вычисления функции
и измеренные значения используются для вычисления функции

а погрешности аргументов независимы и случайны, то погрешность в  равна квадратичной сумме исходных погрешностей:
равна квадратичной сумме исходных погрешностей:
 (1.22)
(1.22)
в любом случае она никогда не больше, чем их обычная сумма

3. Погрешности в произведениях и частных. Если величины  измерены с малыми погрешностями
измерены с малыми погрешностями  и измеренные значения используются для вычисления функции
и измеренные значения используются для вычисления функции

а погрешности аргументов независимы и случайны, то относительная погрешность в Z равна квадратичной сумме исходных относительных погрешностей:
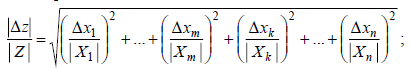 (1.24)
(1.24)
в любом случае она никогда не больше, чем их обычная сумма
 (1.25)
(1.25)
4. Погрешность в произвольной функции одной переменной. Если величина  измерена с погрешностью
измерена с погрешностью  и используется для вычисления функции
и используется для вычисления функции  , то абсолютная погрешность в
, то абсолютная погрешность в  равна
равна
 (1.26)
(1.26)
5. Погрешность в степенной функции. Если величина X измерена с погрешностью  и используется для вычисления степенной функции
и используется для вычисления степенной функции 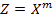 (где
(где 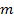 — фиксированное известное число), относительная погрешность в
— фиксированное известное число), относительная погрешность в  в
в 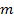 раз больше, чем в
раз больше, чем в  :
:

Пользуясь формулами (1.21) - (1.27), можно справиться практически с любой задачей вычисления ошибок в случае косвенных измерений. Любой расчет может быть представлен как последовательность определенных шагов, каждый из которых включает один из следующих видов операций: 1) нахождение сумм и разностей, 2) расчет произведений и частных, 3) вычисление функции одного переменного
(данный метод называют «шаг за шагом»). Однако в случае когда выражение для вычисления функции Z включает одну и ту же величину более чем один раз (например, дважды  ), то некоторые из ошибок могут взаимно компенсироваться и в результате расчет ошибки методом «шаг за шагом» может привести к переоценке конечной погрешности. Поэтому в подобных случаях рекомендуется пользоваться общими формулами (1.19) и (1.20).
), то некоторые из ошибок могут взаимно компенсироваться и в результате расчет ошибки методом «шаг за шагом» может привести к переоценке конечной погрешности. Поэтому в подобных случаях рекомендуется пользоваться общими формулами (1.19) и (1.20).
|
из
5.00
|
Обсуждение в статье: Приближенных аргументов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

