 |
Главная |
Порядок перевода целых двоичных чисел в десятичную систему счисления
|
из
5.00
|
0 1 2 3 4 5 6 7 8 9
Приведенное в качестве примера число 272,12 представляет собой краткую запись многочлена
272,12=2·102+7·101+2·100+1·10–1+2·10–2
Место, которое цифра занимает в числе, называют разрядом. Разрядам принято присваивать номера. Номер разряда равен показателю степени, в которую в приведенном примере возводится число 10. Разряд с большим номером принято называть старшим, разряд с меньшим номером – младшим. Номера разрядов дробной части числа записываются отрицательными числами.
Число 10 следует за числом 9 и, чтобы его получить, надо к числу 9 добавить еще одну единицу. В принятой системе нет специальной цифры для записи такого числа, но есть правила, позволяющие записать это число с помощью имеющихся цифр. При его записи появляется единица старшего разряда, а в младшем записывается 0. В данной системе счисления число 10 является ее основанием. Часть разрядов в этой системе имеют свои названия: разряд единиц, десятков, сотен и т.д.
Основанием системы счисленияназывают минимальное число, при записи которого появляется цифра в 1-м разряде.
Основанием определяется название системы счисления. Поэтому рассматриваемая система называют десятичной позиционной системой счисления.
Все позиционные системы сходны по правилам записи чисел.
Выбор в пользу той или иной системы счисления – выбор исторический. Принципиально основанием системы счисления может являться любое натуральное число.
Вернемся к понятию «число» и сделаем несколько некоторых общих замечаний:
- любое число имеет значение (обозначает определенное количество);
- любое число имеет форму представления (записывается по определенным правилам).
Значение числа задает его отношение к значениям других чисел (больше, меньше, равно) и, следовательно, порядок его расположения в ряду чисел (на числовой оси).
Форма представления определяет порядок записи чисел с помощью предназначенных для этого знаков.
При этом значение числа является инвариантом, т.е. не зависит от способа представления. Это означает, что число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие между представлением числа и его значением
Двоичная система счисления.
Это позиционная система счисления с основанием 2. Любое число в двоичной системе записывается с помощью всего двух знаков: «0» и «1».
Начало двоичной системе счисления было положено в 1666 году работой выпускника университета Готфрида Вильгельма Лейбница, впоследствии гениального немецкого ученого. Работа называлась «Искусство составления комбинаций» и была посвящена проблеме трансформации человеческих мыслей в точные формальные высказывания.
Идея Лейбница оказалась невостребованной при его жизни, однако почти два века спустя англи йский математик-самоучка Джордж Буль продолжил исследования Лейбница. В 1847 году он публикует статью «Математический анализ логики», а в 1854 году выходит его работа «Исследование законов мышления». Эти работы положили начало новой науки: алгебры логики. Ее языком была двоичная система счисления.
Порядок перевода целых десятичных чисел в двоичную систему счисления.
Алгоритм перевода целого десятичного числа в новую позиционную систему счисления одинаков при любом основании этой новой системы. Его словесное описание приведено ниже.
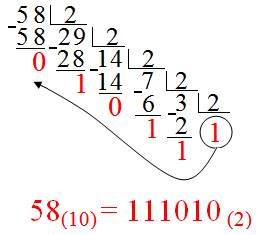 Перевод целых десятичных чисел в новую позиционную систему счисления осуществляется методом последовательного целочисленного деления исходного числа на основание новой системы счисления. Деление продолжается до тех пор, пока полученное частное не окажется меньше делителя (основания новой системы счисления). Цифрами нового кода являются полученные в процессе деления остатки и последнее частное. Цифрой старшего разряда нового кода является последнее частное. К ней последовательно дописываются остатки от последнего до первого. Все действия выполняются по законам десятичной арифметики.
Перевод целых десятичных чисел в новую позиционную систему счисления осуществляется методом последовательного целочисленного деления исходного числа на основание новой системы счисления. Деление продолжается до тех пор, пока полученное частное не окажется меньше делителя (основания новой системы счисления). Цифрами нового кода являются полученные в процессе деления остатки и последнее частное. Цифрой старшего разряда нового кода является последнее частное. К ней последовательно дописываются остатки от последнего до первого. Все действия выполняются по законам десятичной арифметики.
Пример использования алгоритма
Порядок перевода целых двоичных чисел в десятичную систему счисления.
Перевод выполняется по правилам десятичной арифметики. Предварительно двоичное число представляется в виде многочлена, каждый элемент которого – произведение двух сомножителей. Первый сомножитель – соответствующая цифра двоичного числа. Второй – степень двойки, показатель которой соответствует номеру разряда рассаматриваемой цифры.
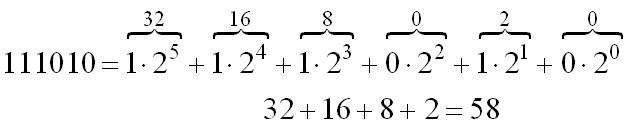

|
из
5.00
|
Обсуждение в статье: Порядок перевода целых двоичных чисел в десятичную систему счисления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

