 |
Главная |
Классическое определение вероятности
|
из
5.00
|
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие.
Вероятность события А обозначается 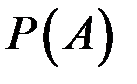 . В соответствии с определением
. В соответствии с определением
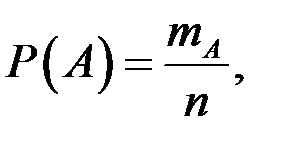
где 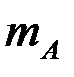 – число элементарных исходов, благоприятствующих событию А, n – число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
– число элементарных исходов, благоприятствующих событию А, n – число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Это определение вероятности называют классическим. При вычислении вероятностей событий с использованием классического определения, могут быть использованы формулы комбинаторики.
Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов.
Число возможных перестановок из n элементов обозначают через 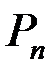 , это число равно n!:
, это число равно n!:
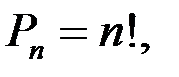
где 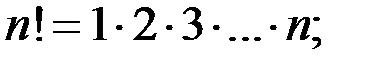 по определению полагают, что
по определению полагают, что 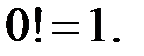
Размещенияминазывают множества, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число всевозможных размещений определяется формулой
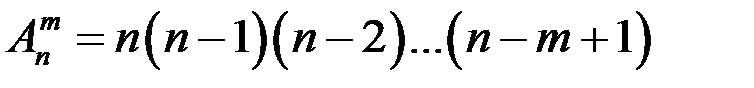 ,
,
или
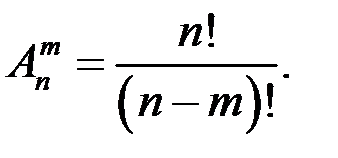
Сочетаниями из n различных элементов по m называются множества, содержащие m элементов из числа n заданных, и которые отличаются хотя бы одним элементом.
Число сочетаний из n элементов по m определяется формулой
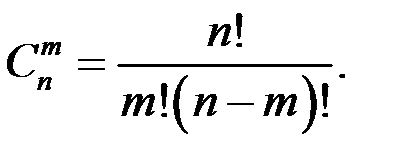
Число перестановок, размещений и сочетаний связаны равенством
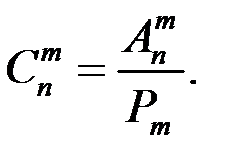
В приведенных формулах предполагалось, что все n элементов различны.
При решении задач комбинаторики используют следующие правила.
Правило суммы.Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно 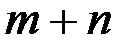 способами.
способами.
Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана 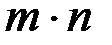 способами.
способами.
Пример 1
В ящике находятся 15 красных, 9 синих и 6 зеленых шаров. Наудачу выбирают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 синих и 3 красных шара (событие А)?
Решение
В ящике всего 30 шаров. При данном испытании число всех равновозможных элементарных исходов будет 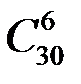 . Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать
. Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать 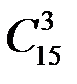 способами, два синих шара из 9 можно выбрать
способами, два синих шара из 9 можно выбрать 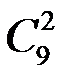 способами, один зеленый из 6 –
способами, один зеленый из 6 – 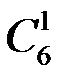 способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет
способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет 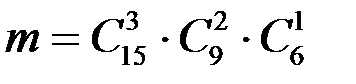 .
.
По формуле 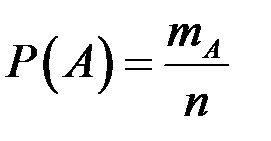 находим искомую вероятность
находим искомую вероятность
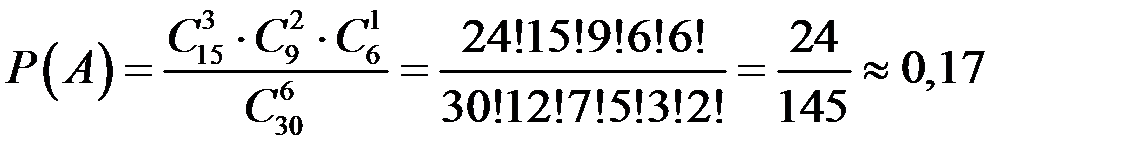 .
.
Пример 2
На пяти одинаковых карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?
Решение
Из пяти различных элементов можно составить 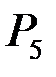 перестановок
перестановок
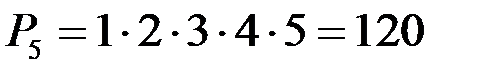 .
.
Значит, всего равновозможных исходов будет 120, а благоприятствующих данному событию – только один. Следовательно,
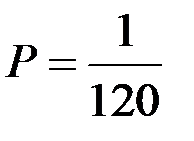 .
.
Пример 3
Набирая номер телефона, абонент забыл последние три цифры и помнил лишь, что эти цифры различные. Найти вероятность того, что набраны нужные цифры.
Решение
Событие А – набраны три нужные цифры. Вероятность 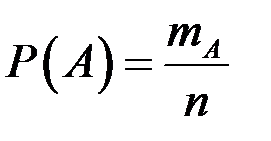 ,
, 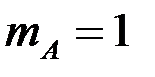 – число исходов, благоприятствующих событию А,
– число исходов, благоприятствующих событию А, 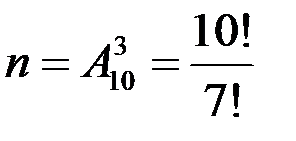 – число всех возможных вариантов набора, поэтому искомая вероятность
– число всех возможных вариантов набора, поэтому искомая вероятность
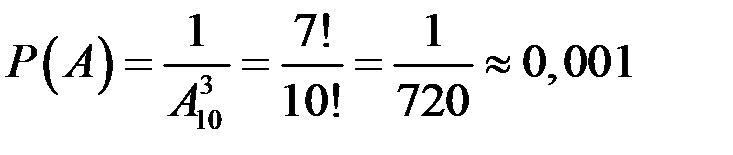 .
.
|
из
5.00
|
Обсуждение в статье: Классическое определение вероятности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

