Метод Драгилева А. В. нахождения решений систем нелинейных уравнений

 

Будем считать, что все переменные определены и действуют в вещественной области, и все действия, выполняемые над ними, допустимы. Рассмотрим систему из n уравнений, в которой количество переменных равно n+1. Такая система описывает некую кривую в пространстве размерности n+1:

 

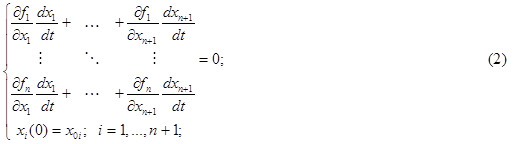Построим кривую (1), предположив, что в качестве независимой переменной выступает длина дуги самой кривой. Координаты точек кривой получим как решение задачи Коши для системы обыкновенных дифференциальных уравнений, начальными данными для которой будут координаты заранее известной точки, принадлежащей этой кривой. Систему дифференциальных уравнений получаем дифференцированием (1) по формальному параметру t и, выбрав начальную точку, заведомо принадлежащую (1), будем решать задачу Коши для координат точек этой кривой:

 

Чтобы применить к (2) численный метод решения дифференциальных уравнений, сначала разрешим её относительно производных. Сделаем это с помощью правила Крамера, приняв за свободную переменную, например, n+1 производную. Зададим её равной главному определителю системы, чтобы избавиться от знаменателей. И вместо (2) получим следующую систему уравнений:

 

 

Из курса математического анализа мы знаем, что длина дуги не зависит от выбора параметра t, и она возрастает вместе с t. Значение t=0 соответствует выбранной начальной точке, от которой кривая будет строиться в обоих направлениях, в “положительном” направлении шаг интегрирования будет положительным, а в “отрицательном” – отрицательным. Для решения (2а) можем применить стандартный алгоритм численного решения задачи Коши, чтобы построить кривую (1).

 

Перейдём теперь к методу Драгилева. Метод развивает идею метода продолжения по параметру. Продолжение по параметру предполагает использование в качестве независимой переменной сам параметр, искусственно введённый в систему или назначенный из числа переменных, находящихся в системе изначально. Возьмём за основу один из самых простых вариантов метода продолжения по параметру. Пусть (3) система уравнений относительно Y:

 

Выберем точку

 

Значение, которое в этой точке примет система (3), будет

 

И рассмотрим новую систему уравнений:

 

В этой системе – параметр, который в случае = 0 обращает (3a) в (3), а в случае, когда равен 1, то в точке

левая часть (3а) обращается в 0. Таким образом, если в (3а) предположить, что:

 

то, изменяя параметр от 1 до 0, можно от решения (3а) прийти к решению (3). Участок кривой, который описывает при этом (3а), должен соответствовать монотонному изменению всех координат. Это более слабое условие, чем для метода Ньютона, но если речь идёт о поиске решения почти “вслепую”, метод продолжения по параметру имеет мало преимуществ перед методами типа метода Ньютона.

Сравним (1) и (3а). Если в (3а) рассматривать в качестве n+1 координаты, то по предложенному выше алгоритму можно построить кривую. Начальным значением для будет 1, а значения остальных координат выбираются как начальная точка для нахождения решения системы нелинейных уравнений (3). В процессе построения кривой может менять знак, это будет означать, что кривая пересекает пространство размерности n, и в этом месте будет область, содержащая решение (3). Количество найденных решений будет соответствовать числу перемен знака параметра. Кривая может проходить точки экстремума. Это позволяет находить решения весьма удалённые от начальной точки и находить более одного решения для одной начальной точки. Можно сказать, метод имеет слабую зависимость от начального приближения.

Оценка точности приближения связана с погрешностью конкретного численного метода решения задачи Коши. Область проекции того участка кривой на пространство размерности n, внутри которого параметр меняет знак от шага m к шагу m+1, содержит решение уравнения. Какую-либо из двух граничных точек, соответствующих шагу m и шагу m+1, можно принимать за приближённое решение. Возможность метода находить более одного решения позволяет организовывать поиск решений по двум направлениям кривой от начальной точки и фиксировать найденные приближения.

 

---------------------------------------------------------------------------------------------

Этот метод был разработан в 1979 году КФМН Драгилевым Анатолием Владимировичем (1923 –1997) г.

---------------------------------------------------------------------------------------------