 |
Главная |
Абсолютная сходимость рядов
|
из
5.00
|
Пример 2.
Исследовать, сходится ли ряд 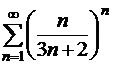 .
.
Поскольку
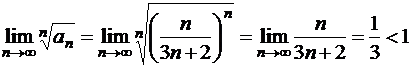 ,
,
 то ряд сходится.
то ряд сходится.
Интегральный признак сходимости
Интегральный признак сходимости выражается следующей теоремой
Теорема 1.8.
Дан ряд с положительными членами
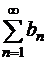
| (1.23) |
и несобственный интеграл
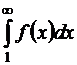 . .
| (1.24) |
Если при 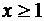 функция
функция 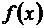 непрерывна, положительна и не возрастает, а в точках
непрерывна, положительна и не возрастает, а в точках 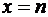 принимает значения
принимает значения 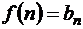 , то ряд (1.23) и несобственный интеграл (1.24) одновременно сходятся или расходятся.
, то ряд (1.23) и несобственный интеграл (1.24) одновременно сходятся или расходятся.
Доказательство.
Если 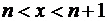 , то
, то 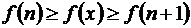 , откуда
, откуда
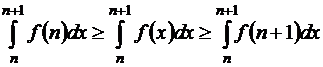 ;
;
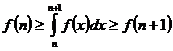 ; ;
| (1.25) |
Суммируя члены неравенства (1.25) от 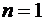 до
до 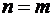 , получаем
, получаем
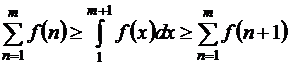 ;
;
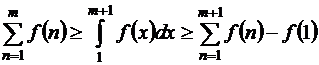
т.е.
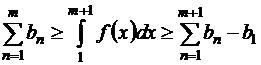
или
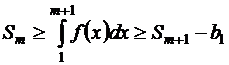 . .
| (1.26) |
Если интеграл (1.24) сходится и 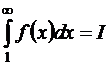 , то
, то 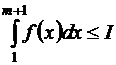 при любом натуральном
при любом натуральном 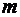 . Следовательно,
. Следовательно,
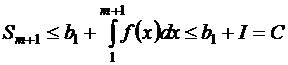
или
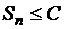
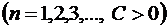 .
.
Так как 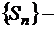 монотонно возрастающая и ограниченная последовательность, то существует
монотонно возрастающая и ограниченная последовательность, то существует 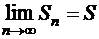 , т.е. ряд (1.23) также сходится. Если ряд (1.23) сходится и
, т.е. ряд (1.23) также сходится. Если ряд (1.23) сходится и 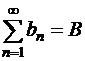 , то
, то 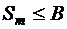 при любом
при любом 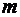 .
.
Из равенства (1.26) следует, что 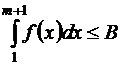 при любом
при любом 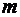 . Несобственный интеграл также сходится.
. Несобственный интеграл также сходится.
С помощью интегрального признака можно доказать, что ряд
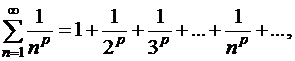
| (1.27) |
где 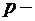 любое вещественное число, сходится при
любое вещественное число, сходится при 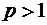 и расходится при
и расходится при 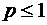 .
.
Действительно, 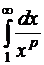 сходится при
сходится при 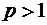 и расходится при
и расходится при 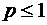 .
.
Знакочередующиеся ряды. Признак Лейбница
Знакочередующимся рядом называется ряд, у которого любые два члена с номерами 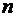 и
и 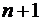
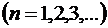 имеют противоположные знаки, т.е. ряд вида
имеют противоположные знаки, т.е. ряд вида
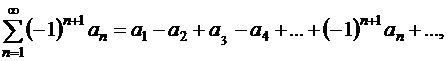
| (1.28) |
где 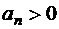
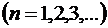 .
.
Теорема 1.9 (признак Лейбница).
Знакочередующийся ряд (1.28) сходится, если модули его членов убывают с возрастанием 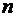 и общий член стремится к нулю, т.е.
и общий член стремится к нулю, т.е.
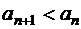 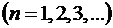
| (1.29) |
и
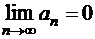
| (1.30) |
Доказательство.
Рассмотрим частичные суммы ряда (1.28) с четными и нечетными номерами:
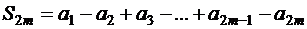 ,
,
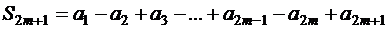 .
.
Преобразуем первую из этих сумм:
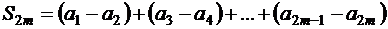
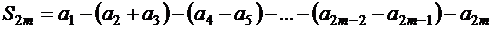 .
.
В силу условия (1.29) разность в каждой скобке положительна, поэтому сумма 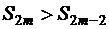 и
и 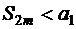 для всех
для всех 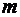 . Итак, последовательность четных частичных сумм
. Итак, последовательность четных частичных сумм 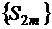 является монотонно возрастающей и ограниченной. Она имеет предел, который обозначим через
является монотонно возрастающей и ограниченной. Она имеет предел, который обозначим через 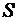 , т.е.
, т.е. 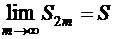 . Поскольку
. Поскольку 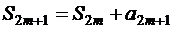 , то, принимая во внимание предыдущее равенство и условие (1.30), получаем
, то, принимая во внимание предыдущее равенство и условие (1.30), получаем
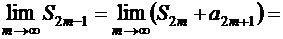
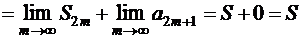 .
.
 Итак, последовательность частичных сумм данного ряда соответственно с четными и нечетными номерами имеют один и тот же предел
Итак, последовательность частичных сумм данного ряда соответственно с четными и нечетными номерами имеют один и тот же предел 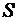 . Отсюда следует, что последовательность всех частичных сумм ряда имеет предел
. Отсюда следует, что последовательность всех частичных сумм ряда имеет предел 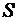 ;
; 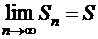 т.е. ряд сходится.
т.е. ряд сходится.
Пример.
Исследовать, сходится ли ряд
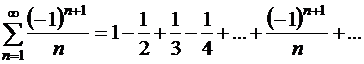
| (1.31) |
Этот ряд является знакочередующимся. Он сходится, поскольку удовлетворяет условиям теоремы

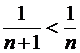

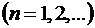 ,
, 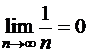 .
.
Оценка остатка знакочередующегося ряда определяется с помощью следующей теоремы.
Теорема 1.10.
Сумма остатка знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, имеет знак первого оставшегося члена и не превосходит его по модулю.
Доказательство.
Рассмотрим остаток ряда (1.28) после 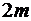 членов. Пусть
членов. Пусть 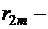 его сумма,
его сумма, 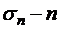 -я частичная сумма, тогда
-я частичная сумма, тогда
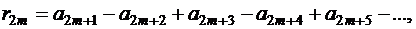
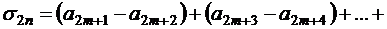
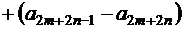 ,
,
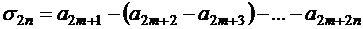
Так как выполнены условия теоремы 1.9, то 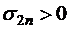 и
и 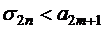 при всех
при всех 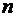 , т.е.
, т.е. 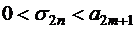
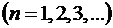 , откуда
, откуда
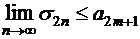 или
или 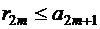
Аналогично доказывается, что сумма 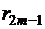 остатка ряда после
остатка ряда после 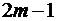 членов
членов 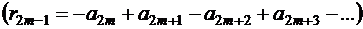 удовлетворяет условиям
удовлетворяет условиям 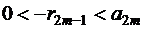 , т.е.
, т.е. 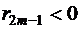 и
и 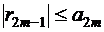 .
.
Следовательно, независимо от четности или нечетности 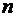
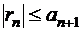
| (1.32) |
Абсолютная сходимость рядов
В этом параграфе будем изучать ряды, члены которых являются действительными числами любого знака. Пусть дан такой ряд
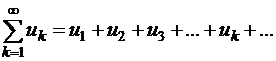 . .
| (1.33) |
Рассмотрим ряд, составленный из модулей членов данного ряда:
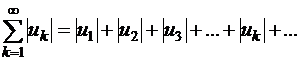
| (1.34) |
Теорема 1.11.
Если ряд (1.34) сходится, то сходится и ряд (1.33).
Доказательство.
Поскольку ряд (1.34) сходится, то в силу критерия Коши (теорема 1.1) для любого 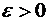 существует такой номер
существует такой номер 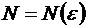 , то при всех
, то при всех 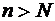 и любом целом
и любом целом 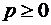 выполняется неравенство
выполняется неравенство
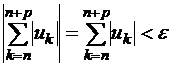
Так как
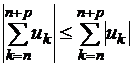 .
.
 то
то 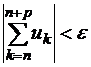 . Это означает, что ряд (1.33) также сходится.
. Это означает, что ряд (1.33) также сходится.
Замечание.
 Из сходимости ряда (1.33) не следует сходимость ряда (1.34). Например, ряд
Из сходимости ряда (1.33) не следует сходимость ряда (1.34). Например, ряд 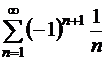 сходится (см. п. 1.6), а ряд из модулей его членов расходится (гармонический ряд, см. п. 1.2).
сходится (см. п. 1.6), а ряд из модулей его членов расходится (гармонический ряд, см. п. 1.2).
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из модулей его членов. Например, ряд
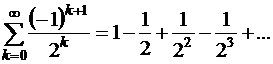
является абсолютно сходящимся, поскольку сходится ряд из модулей его членов, т.е. ряд 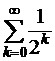 (геометрическая прогрессия со знаменателем
(геометрическая прогрессия со знаменателем 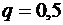 ,
, 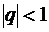 ).
).
Знакопеременный ряд называется неабсолютно сходящимся (условно сходящимся), если он сходится, а ряд из модулей его членов расходится. Например, ряд 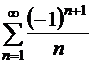 является неабсолютно сходящимся (см. замечание).
является неабсолютно сходящимся (см. замечание).
Действия над рядами.
Произведением ряда
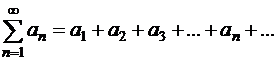
| (1.35) |
на число с называется ряд
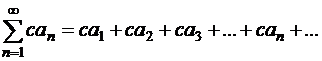
| (1.36) |
Теорема 1.12.
Если ряд (1.35) сходится, то ряд (1.36) также сходится, причем
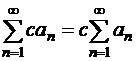
| (1.37) |
Доказательство.
Обозначим через 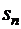 и
и 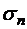
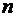 - е частичные суммы рядов (1.35) и (1.36), т.е.
- е частичные суммы рядов (1.35) и (1.36), т.е.
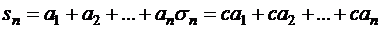
Очевидно, 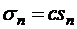 . Если ряд (1.35) сходится и его сумма равна
. Если ряд (1.35) сходится и его сумма равна 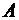 , т.е.
, т.е. 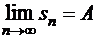 ,
, 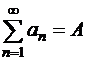 , то
, то
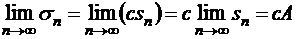
т.е.
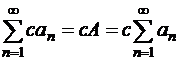
Кроме ряда (1.35) рассмотрим ряд
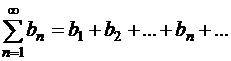
| (1.38) |
Суммой двух рядов (1.35) и (1.38) называется ряд
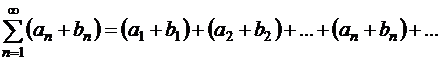 . .
| (1.39) |
Аналогично определяется разность рядов (1.35) и (1.38):
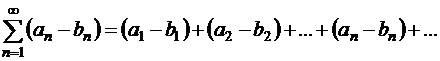 . .
| (1.40) |
Теорема 1.13.
Если сходятся ряды (1.35) и (1.38) , то сходится их сумма и разность, причем
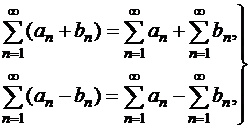
| (1.41) |
Доказательство.
Обозначим соответственно через 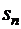 ,
, 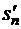 ,
, 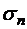
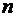 - е частичные суммы рядов (1.35), (1.38), (1.39):
- е частичные суммы рядов (1.35), (1.38), (1.39):

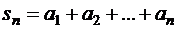 ,
, 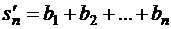 ,
,
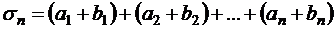 .
.
Очевидно, 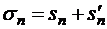 . Если ряды (1.35) и (1.38) сходятся, т.е.
. Если ряды (1.35) и (1.38) сходятся, т.е.
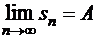 ,
, 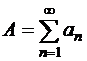 ,
, 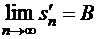 ,
, 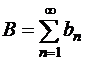
то
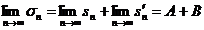 ,
, 
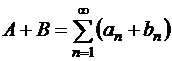 ,
,
или
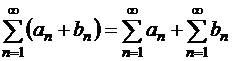 .
.
Аналогично доказывается второе из равенств (1.41).
Произведением двух рядов (1.35) и (1.38) называется ряд
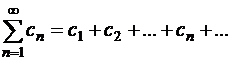 , ,
| (1.42) |
где
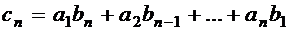 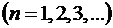 . .
| (1.43) |
Отметим без доказательства, что если ряды (1.35) и (1.38) сходятся абсолютно, то их произведение, т.е. ряд
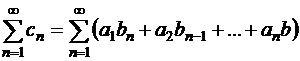
| (1.44) |
также сходится абсолютно и его сумма равна 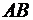
Замечание.
Правила действия над рядами не всегда совпадают с правилами действий над конечными суммами. В частности, в конечных суммах можно произвольно менять порядок слагаемых, как угодно группировать члены, сумма от этого не изменится. Слагаемые конечной суммы можно складывать в обратном порядке, для ряда такой возможности нет, ибо у него не существует последнего члена.
В ряде не всегда можно группировать члены. Например, ряд
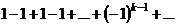
является расходящимся, так как
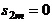
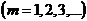 ,
, 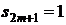
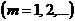
и нет предела его частичных сумм. После группировки членов
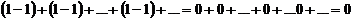
получаем сходящийся ряд, его сумма равна нулю. При другой группировке членов
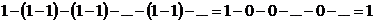
получаем сходящийся ряд, сумма которого равна единице.
Приведем без доказательства две теоремы.

Теорема 1.14.
Перестановка членов абсолютно сходящегося ряда не нарушает его сходимости, сумма ряда при этом остается прежней.
Теорема 1.15.
Если ряд сходится неабсолютно, то путём надлежащей перестановки его членов всегда можно придать сумме ряда произвольное значение и даже сделать ряд расходящимся.
|
из
5.00
|
Обсуждение в статье: Абсолютная сходимость рядов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

