 |
Главная |
Бинарные отношения и их свойства.
|
из
5.00
|
Рзадел 1. Вопрос 13.
Понятие соответствия. Способы задания соответствия. Взаимно однозначное соответствие. Функциональное соответствие.
Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.

В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.
Что общее имеют эти соответствия?
Видим, что во всех случаях мы имеем два множества: в первом - это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений), во втором - это множество из трех геометрических фигур и множество N натуральных чисел; в третьем - это множество из трех уравнений и множество N натуральных чисел.
Выполняя предложенные задания, мы устанавливаем связь (соответствие) между элементами этих множеств. Ее можно представить наглядно, при помощи графов (рис. 1).

Можно задать эти соответствия, перечислив все пары элементов, находящихся в заданном соответствии:
I. {(в1, 4), (в3, 20)};
II. {( F1, 4), (F2, 10), (F3, 10)};
III. {(у1, 4), (у2, 11), (у3, 4)}.
Полученные множества показывают, что любое соответствие между двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары - это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
Определение. Соответствием между элементами множество X и Y называется всякое подмножество декартова произведения этих множеств.
Соответствия принято обозначать буквами Р, S, T, R и др. Если S - соответствие между элементами множеств X и Y, то, согласно определению, S 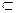 Х х Y.
Х х Y.
Выясним теперь, как задают соответствия между двумя множествами. Поскольку соответствие - это подмножество, то его можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества. Так, соответствие между множествами X = {1, 2, 4, 6} и Y = {3, 5} можно задать:
1) при помощи предложения с двумя переменными: а < b при условии, что а  X, b
X, b  Y;
Y;
2) перечислив пары чисел, принадлежащих подмножеству декартова произведения XxY: {(1, 3), (1, 5), (2, 3), (2, 5), (4, 5)}. К этому способу задания относят также задание соответствия при помощи графа (рис. 2) и графика (рис. 3)

Определение. Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при котором каждому элементу множества X сопоставляется единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.
Рассмотрим примеры взаимно однозначных соответствий.
Пример 1. Пусть Х - множество кружков, У- множество квадратов и соответствие между ними задано при помощи стрелок (рис. 6).

Рис.6
Это соответствие взаимно однозначное, так как каждому кружку из множества X сопоставляется единственный квадрат из множества Y и каждый квадрат из Y соответствует только одному кружку из множества X.
Пример 2. Пусть Х- множество действительных чисел, Y- множество точек координатной прямой. Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Это соответствие взаимно однозначное, так как каждому действительному числу сопоставляется единственная точка координатной прямой и каждая точка на" прямой соответствует только одному числу.
В математике взаимно однозначное соответствие между элементами множеств X и Y часто называют взаимно однозначным отображением множества X на множество Y.
Понятие взаимно однозначного соответствия позволяет определить отношение равномощности множеств.
Определение. Множества X и Y называются равномощными, если между элементами можно установить взаимно однозначное соответствие.
Если множества Х и Y равномощны, то пишут X ~ Y.
Нетрудно увидеть, что множества, которые были рассмотрены в примерах 1 и 2, равномощны.
Равномощными могут быть как конечные, так и бесконечные множества. Равномощные конечные множества называют ещё равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими другими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие.
Функциональным соответствием между множествами X и Y называют такое соответствие, при котором каждому элементу из множества X сопоставляется не более одного элемента из множества Y. Примером функциональных соответствий могут служить соответствия, графы которых изображены на рисунке.

Частным случаем функционального соответствия междумножествами X и Y является соответствие, при котором каждому элементу из множества X сопоставляется точно один элемент из множества Y. Такое соответствие называется отображением множества X во множество Y.
Раздел 1. Вопрос 14.
Понятие функции. Способы задания функций. Прямая и обратная пропорциональность, их свойства и графики.
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут  , при этом x называют аргументом функции, y называют значением функции.
, при этом x называют аргументом функции, y называют значением функции.
Существуют разные способы задания функций.
1. Аналитический способ.
Аналитический способ - это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например 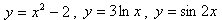 .
.
Рассмотрим первый пример -  . Здесь значению x = 1 соответствует
. Здесь значению x = 1 соответствует  , значению x = 3 соответствует
, значению x = 3 соответствует  и т. д.
и т. д.
Функция может быть задана на разных частях множества X разными функциями.
Например:

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например  . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
. Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
 . То есть, значение функции при х = 3 равно -4/3.
. То есть, значение функции при х = 3 равно -4/3.
При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом  . Пример:
. Пример:

3. Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
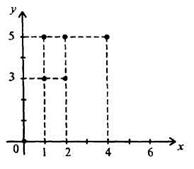
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком
Определение. Прямой пропорциональностью называется функция, которая может быть задана при помощи формулы у = kx, где k не равное нулю действительное число.
Название функции у = kх связано с тем, что в формуле у = kх есть переменные х и у, которые могут быть значениями величин. А если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае  .
.
Это число называют коэффициентом пропорциональности.
Функция у = kх является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана выше. пример: если в одном пакете муки 2 кг, а куплено х таких пакетов, то всю массу купленной муки (обозначим ее через у) можно представить в виде формулы у = 2х, т. е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k = 2.
Напомним некоторые свойства прямой пропорциональности:
1. Областью определения функции у = kх и областью ее значений является множество действительных чисел.
2. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Поэтому для построения графика прямой пропорциональности достаточно найти лишь одну точку, принадлежащую ему и не совпадающую с началом координат, а затем через эту точку и начало координат провести прямую.
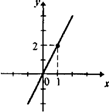
Например, чтобы построить график функции у = kх, достаточно иметь точку с координатами (1,2), а затем через нее и начало координат провести прямую (рис. 7).
3. При k > 0 функция у = kх возрастает на всей области определения, при k < 0 — убывает на всей области определения.
4. Если функцияf - прямая пропорциональность и (х1, у1), (х2, у2) -пары соответственных значений переменных х и у, причем х2¹0, то 
Действительно, если функция f - прямая пропорциональность, то она может быть задана формулой у = kх, и тогда у1 = kх1, у2 = kх2 . Так как х2 ¹ 0 и k¹0, то у2¹0. Поэтому 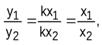 и значит
и значит 
Определение. Обратной пропорциональностью называется функция, которая может быть задана при помощи формулы  гдеk - не равное нулю действительное число.
гдеk - не равное нулю действительное число.
Название данной функции связано с тем, что в  есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности.
есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности.
Функция  является математической моделью многих реальных ситуации, рассматриваемых уже в начальном курсе математики.
является математической моделью многих реальных ситуации, рассматриваемых уже в начальном курсе математики.
Одна из них описана перед определением обратной пропорциональности.
пример: если купили 12 кг муки и разложили ее в х пакетов по у кг в каждую, то зависимость между данными величинами можно представить в виде х×у = 12, т.е. она является обратной пропорциональностью с коэффициентом k = 12. Напомним некоторые свойства обратной пропорциональности, известные из школьного курса математики.
1. Областью определения функции  областью ее значений х является множество действительных чисел, отличных от нуля.
областью ее значений х является множество действительных чисел, отличных от нуля.
2. Графиком обратной пропорциональности является гипербола.
3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция  является убывающей на всей области определения х (рис.8). При k < 0 ветви гиперболы расположены во 2-й и 4-й четверти функция
является убывающей на всей области определения х (рис.8). При k < 0 ветви гиперболы расположены во 2-й и 4-й четверти функция  является возрастающей на всей области определения х (рис. 9).
является возрастающей на всей области определения х (рис. 9).
 у у
у у
k > 0 k < 0
х х
Рис. 8 Рис. 9
4. Если функция f – обратная пропорциональность и (х1, у1), (х2, у2) – пары соответствующих значений переменных х и у, то 
Действительно, если функция f - обратная пропорциональность, она может быть задана формулой  и тогда
и тогда  ,
,  . Так как х1¹0, х2¹0, то
. Так как х1¹0, х2¹0, то  .
.
Раздел 1. Вопрос 15.
Понятие бинарного отношения; способы задания отношений. Свойства бинарных отношений.
Бинарные отношения и их свойства.
Пусть А и В это множества производной природы, рассмотрим упорядоченную пару элементов (а, в) а ϵ А, в ϵ В можно рассматривать упорядоченные «энки».
(а1, а2, а3,…аn), где а1 ϵ А1; а2 ϵ А2; …; аn ϵ Аn ;
Декартовым (прямым) произведением множеств А1, А2, …, Аn , называется мн-во, которое состоит из упорядоченных nk вида  .
.
Н-р: М = {1,2,3}
М× М= М2 = {(1,1);(1,2);(1,3); (2,1);(2,2);(2,3); (3,1);(3,2);(3,3)}.
Подмножества декартова произведения  называется отношением степени nили энарным отношением. Если n=2, то рассматривают бинарные отношения. При чем говорят, что а1, а2 находятся в бинарном отношении R, когда а1 R а2.
называется отношением степени nили энарным отношением. Если n=2, то рассматривают бинарные отношения. При чем говорят, что а1, а2 находятся в бинарном отношении R, когда а1 R а2.
Бинарным отношением на множестве M называется подмножество прямого произведения множества n самого на себя.
М× М= М2 = {(a, b)| a, b ϵ M} в предыдущем примере отношение меньше на множестве Мпорождает следующее множество: {(1,2);(1,3); (2,3)}
Бинарные отношения обладают различными свойствами в том числе:
· Рефлексивность: 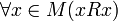 .
.
· Антирефлексивность (иррефлексивность):  .
.
· Симметричность: 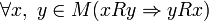 .
.
· Антисимметричность:  .
.
· Транзитивность:  .
.
· Асимметричность: 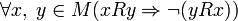 .
.
|
из
5.00
|
Обсуждение в статье: Бинарные отношения и их свойства. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

