Распределение Вейбулла

Содержание

Задание 1

 

Определить основные свойства и характеристики потоков вызовов со следующими законами распределения интервалов между вызовами (интенсивность простейшего потока 6 вызовов/час).

 

· Простейший поток

· Распределение Эрланга

· Распределение Вейбулла

· Гамма распределение

· Распределение Парето

 

Построить графики распределений. Сравнить свойства потоков.

 

Решение:

Простейший поток

Простейшим потоком называется стационарный (параметр потока, а также вероятности состояний не зависят от времени), однородный (свойства всех вызовов одинаковы), ординарный (одновременно не может поступить более одного вызова), без последействия (вероятности состояний не зависят от предыстории) поток от бесконечного числа источников с експоненцальным распределением вероятности интервалов между вызовами.

Функция плотности вероятности интервалов между вызовами:

 

Рисунок 1- Функция плотности распределения вероятности интервалов между вызовами для простейшего потока

Функция вероятности интервалов между вызовами:

 

Рисунок 2 - Функция распределения вероятности интервалов между вызовами

для простейшего потока

 

Из данного распределения видно, что вероятность нулевого интервала между вызовами равна нулю, что говорит об ординарности простейшего потока.

Математическое ожидание интервалов между вызовами:

 

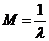
ч

 

Вероятность поступления k вызовов за отрезок времени t:

 

 

Рисунок 3- Вероятности поступления k вызовов за интервалы времени 0,5М, М и lМ.

 

Как видно из графика на рисунке 3, за время равное математическому ожидания наиболее вероятно поступление одного вызова А за время равное

- наиболее вероятно поступление 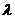вызовов. Данные вероятности не зависят от начала отсчета времени, а зависят лишь от промежутка рассматриваемого времени (это доказывает свойство стационарности данного потока).

 

 

Поток Эрланга

Потоком Эрланга порядка r называется поток, полученный следующим образом: простейший поток, в котором (r-1) вызовов потока теряются, r - ый вызов просеивается и т. д.

В общем виде функция плотности распределения вероятности интервалов между вызовами имеет следующий вид:

 

 

Рисунок 4 – Графики функций плотности распределения вероятности интервалов между вызовами для потока Эрланга для различных r (1,10,100)

 

Графики на рисунке 4 показывают последовательный переход распределения Эрланга из показательного (r=1), в детерминированное (при стремлении r в бесконечность). Данный переход можно увидеть и при рассмотрении функции распределения вероятности между вызовами потока Эрланга, которая описывается по следующей формуле:

 

Рисунок 5 – Графики функций распределения вероятности интервалов между вызовами для потока Эрланга для различных r (1,10,100)

 

Из вышеописанного следует, что математическое ожидание интервала между вызовами для потока Эрланга совпадает с математическим ожиданием для простейшего потока и всегда равно 1/λ, следовательно поток Эрланга – ординарный.

 

Гамма распределение

 

Функция плотности вероятности имеет вид:

 

,

где , - Гамма функция.

Для гамма распределения параметр k лежит в пределах от нуля до бесконечности.

Построим графики функции плотности вероятности для различных значений k:

 

Рисунок 6 – Функции плотности распределения вероятности интервалов между вызовами для потока c Гамма - распределением для различных k (0.8,1,10,100)

 

Из графиков на рисунке 6 видно что при стремлении r к бесконечности Гамма распределение вырождается в детерминированное.

 

Рисунок 7 –Функции плотности распределения вероятности интервалов между вызовами для потока c Гамма - распределением для различных k (0.8,1) построенные в логарифмическом масштабе

 

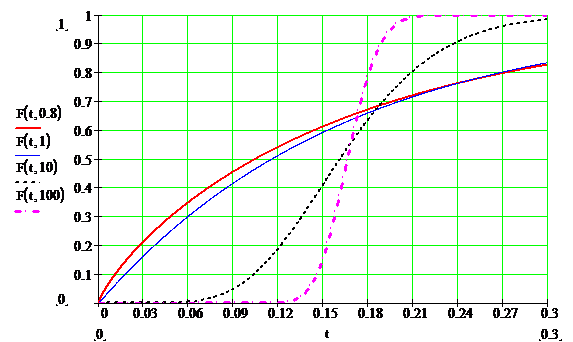
Рисунок 8 –Функции распределения вероятности интервалов между вызовами для потока c Гамма - распределением для различных k (0.8,1,10,100)

 

Из графиков видно что при k<1 гамма распределение обладает, так называемым, «тяжелым хвостом», поток с Гамма-распределением промежутков между вызовами – ординарный, математическое ожидание постоянно при любом k.

 

Распределение Вейбулла

 

Функция плотности вероятности:

 

Рисунок 9 –Функции плотности распределения вероятности интервалов между вызовами для потока c распределением Вейбулла для различных k (0.8,1,10,20)

 

Из рисунков отчетливо видно что при k=1 распределение Вейбулла переходит в показательное и при увеличении k стремится перейти в детерминированное, при k<1 распределение имеет «тяжелый хвост».

 

Рисунок 10 –Функции плотности распределения вероятности интервалов между вызовами для потока c распределением Вейбулла для различных k (0.8,1), построенные в логарифмическом масштабе.

 

Рисунок 11 – Функции распределения вероятности интервалов между вызовами для потока c распределением Вейбулла для различных k (0.8,1,10,20)

 

Как видно из этих графиков, распределение Вейбулла при k=1 переходит в показательное, а при - в детерминированное. При k<1 распределение имеет т. н. «тяжелый хвост».

Математическое ожидание распределения Вейбулла:

 

.

 

При k=1 как и при показательном распределении. При больших k математическое ожидание также равно , а закон распределения переходит в детерминированный.

 

 

Распределение Парето

 

Функция плотности вероятности имеет вид:

 

 

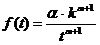
Построим графики функции плотности вероятности при k=2 в зависимости от коэффициента самоподобия H, учитывая, что и .

Функция :

 

Рисунок 12- Функции плотности вероятности для распределения Парето, при k==2, в зависимости от коэффициента подобия.

 

Математическое ожидание:

 

.

 

 

Задание 2

Определить среднюю и расчетную интенсивность поступающей нагрузки на АТС двумя методами (точным и приближенным). Сравнить результаты.

 

Исходные данные:

Население города: до 20 тыс. чел.

Число абонентов квартирного сектора: чел.

Число абонентов производственно-коммерческого сектора: чел.

Число таксофонов: шт.

Среднее число вызовов для квартирного сектора: выз/ч

Среднее число вызовов для производственно-коммерческого сектора: выз/ч

Среднее число вызовов для таксофонов: выз/ч

Средняя длительность разговора для квартирного сектора: сек.

Средняя длительность разговора для производственно-коммерческого сектора: сек.

Средняя длительность разговора для таксофонов: сек

Вероятность разговора: .

 

Решение:

 

Средняя нагрузка, поступающая на АТС от k категорий источников нагрузки, определяется как:

,

где - число источников нагрузки i–ой категории, - интенсивность поступления вызовов от источников i–ой категории, - среднее время обслуживания одного источника i–ой категории.

Среднее время обслуживания складывается из нескольких составляющих в зависимости от того, чем окончилось установление соединения и определяется как:

 

,

 

где , , , , - среднее время обслуживания одного источника вызова при состоявшемся разговоре, занятости вызываемого абонента, неответе вызываемого абонента, ошибки вызывающего абонента, технических неполадках на АТС соответственно и , , , , - вероятности этих событий.

Данные параметры различны для разных групп абонентов.

Найдем составляющие, входящие в формулу для среднего времени обслуживания вызова.

1. Если соединение окончилось разговором, то

 

,

где - время слушания сигнала «ответ станции», - время установления соединения, - время посылки вызова вызываемому абоненту, - время разговора.

с

,

где m – нумерация, принятая на ГТС. Так как емкость АТС до 10 000 абонентов и таких АТС в городе одна, то нумерацию возьмем четырехзначную, т.е. m=4.

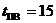с

с

Время разговора зависит от группы источников.

Рассчитаем для различных групп источников.

- для квартирного сектора

с

- для производственно-коммерческого сектора

с

- для таксофонов

с

 

2. Если соединение окончилось тем, что вызываемый абонент оказался занятым или заняты промежуточные линии.

 

,

 

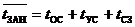Данная составляющая будет одной и той же для разных групп абонентов

 

с

 

3. Соединение не состоялось по причине неответа вызываемого абонента

Для этого случая среднее время обслуживания принимается равным

с.

 

4. Разговор не состоялся из-за ошибки вызывающего абонента.

 

Для этого случая среднее время обслуживания принимается равным

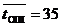с.

 

5. Разговор не состоялся из-за неисправностей на АТС.

 

Для этого случая среднее время обслуживания принимается равным

 

с.

 

В итоге:

 

,

 

- для квартирного сектора

 

с

 

- для производственно-коммерческого сектора

с

- для таксофонов

с

Общие параметры для всех групп:

 

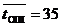с

с

с

с

 

Вероятности данных исходов:

 

 

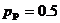
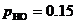
В сумме данные вероятности дают 1.

 

Найдем среднее время обслуживания абонентов различных групп:

 

- для квартирного сектора

с

- для производственно-коммерческого сектора

с

- для таксофонов

с

Определяем среднюю интенсивность нагрузки:

 

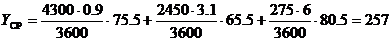Эрл.

Рассчитанная интенсивность нагрузки:

Подставляем значение и получаем:

Эрл.

Рассчитаем нагрузку приближенным способом

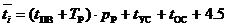
- для квартирного сектора

с

- для производственно-коммерческого сектора

с

- для таксофонов

с

Определяем среднюю интенсивность нагрузки:

Эрл.

Рассчитанная интенсивность нагрузки:

Эрл.

 

Как видно из полученных результатов точный и приближенный метод имеют небольшие расхождения. По затратам сил и времени, занимаемым на вычисления, приближенный метод более предпочтительней.

 

 

Задание 3

 

На полнодоступный пучок линий емкостью V линий поступает поток вызовов от N источников со средним числом вызовов поступающих в ЧНН c. Средняя продолжительность обслуживания одного вызова равна t. Система с явными потерями.

Определить в случае простейшего и примитивного потоков вызовов:

 

· Вероятность потерь по вызовам

· Вероятность потерь по времени

· Вероятность потерь по нагрузке

 

Построить зависимость pi как функцию от i.

Сравнить полученные результаты.

 

Исходные данные:

 

линий

абонентов

выз/ч

с

 

Решение:

 

При поступлении простейшего потока на коммутационную систему вероятность занятия i выходов определяется по первой формуле Эрланга:

,

где y – интенсивность поступающей нагрузки, ν– число линий на выходе коммутационной системы.

Для определения данных вероятностей необходимо найти нагрузку, поступающую на коммутационную систему.

Поступающую нагрузку находим по теореме о поступающей нагрузке:

 

Эрл.

 

Подставляем значение нагрузки в формулу Эрланга и определяем вероятности:

 

Вероятности потерь по времени, вызовам и нагрузке для простейшего потока равны и равны вероятности занятия всех линий в пучке.

 

 

График зависимостей Pi от i:

 

 

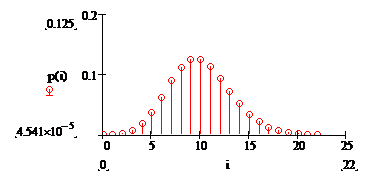
Рисунок 13 - Функция распределения плотности вероятности

 

Из графика видно, что наиболее вероятные состояния системы находятся в области значений i равным интенсивности поступающей нагрузки.

 

При обслуживании примитивного потока вызовов вероятности состояний системы определяются формулой Энгсета:

 

,

 

где N – число источников нагрузки, - удельная нагрузка, приходящаяся на один источник.

 

.

Определим удельную нагрузку:

Эрл.

Потери по времени равны вероятности того, что все линии заняты:

.

Потери по времени:

 

 

 

Потери по нагрузке:

 

 

 

 

Функция распределения плотности вероятности:

Рисунок 14 - Функция распределения плотности вероятности

 

Из графика видно, что наиболее вероятное состояние системы находится в области значений i равным интенсивности поступающей нагрузки, так же как и для случая обслуживания простейшего потока. Однако, сравнивая вероятности потерь для простейшего и примитивного потоков, видим, что потери во втором случае меньше. Таким образом, примитивный поток считается «предпочтительней» простейшего.

 

 

Задание №4

Дано:

· Полнодоступный пучок линий

· Простейший поток вызовов

· Закон распределения длительности обслуживания – показательный

· Система с условными потерями

 

Определить вероятностно-временные характеристики: вероятность потерь по времени, среднюю длительность начала обслуживания, среднюю длину очереди

Построить распределение вероятностей состояний системы и функцию распределения времени ожидания.

Сравнить системы с явными и условными потерями по пропускной способности.

 

Исходные данные такие же, как и в 3 задаче.

Вероятности состояний такой системы находятся по формуле:

 

 

Рисунок 15 - Функция распределения плотности вероятности

 

 

Определим вероятность потерь по времени:

 

- вероятность потерь по времени для системы с явными потерями.

- интенсивность поступающей нагрузки.

- число линий.

 

.

 

Среднее время ожидания:

 

,

где - вероятность потерь по времени, с – среднее время обслуживания вызова, - число линий, - интенсивность поступающей нагрузки.

 

с.

 

Средняя очередь:

Функция распределения времени ожидания:

 

Получаем:

 

 

 

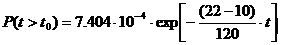
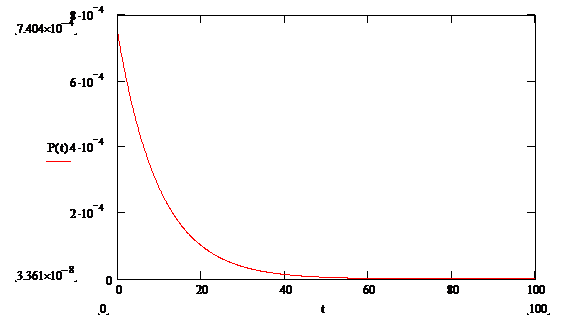
Рисунок 16 - Функция распределения плотности вероятности времени задержки

 

Поскольку вероятность нахождения системы в состоянии, когда мгновенно обслуживаются все вызовы в системе с ожиданием меньше, чем в системе с потерями, то первая обладает меньшей пропускной способностью, чем вторая.

Таким образом, систему с явными потерями рационально использовать в условиях, когда снижение качество обслуживания не критично для абонентов, а систему с условными потерями – при большем количестве заявок.

 

 

Задание №5

Оптимизировать структуру неполнодоступного включения по пропускной способности методом О’Делла и методом оптимизирующих коэффициентов. Построить схему неполнодоступного включения. Привести матрицу связностей. Сделать вывод о ее оптимальности и в случае необходимости провести выравнивание перехватами.

 

Исходные данные:

 

- доступность

- число нагрузочных групп

- общее число линий

 

Решение:

 

Метод О’Дела:

 

Сущность метода заключается в решении системы линейных уравнений:

 

 

Где - число шагов искания, в которых каждый выход объединяет по линий.

Из всех решений выбирается то, для которого выполняется условие:

 

 

То есть

 

Решая систему и проверяя данное условие, определяем, что для приведенного случая:

- 1 шаг искания с 4-мя линиями

- 3 шага искания с 2-мя линиями

- 8 шагов искания с 1-ой линией

 

Метод оптимизирующих коэффициентов:

 

- число линий на j-ом шаге искания.

 

Таблица №1

 

	0,1603	0,1205	0,1042	0,0956	0,0886	0,0818
	2,885	2,169	1,876	1,721	1,595	1,472
округленное

 

	0,0751	0,0683	0,0616	0,0548	0,0481	0,0413
	1,352	1,229	1,109	0,986	0,866	0,743
округленное

 

 

Из сравнения полученных результатов, видно, что решения абсолютно одинаковы.

 

Схема неполнодоступного включения:

Рисунок 16 – Ступенчатая схема объединения выходов

 

Определим матрицу связности для такого включения линий:

 

Из матрицы видно, что связность между различными группами отличается максимум на 3 единицы, что говорит о неоптимальности построенной схемы.

 

Произведем выравнивание.

 

 

Рисунок 17 – Объединение выходов перехватами (выравненная схема)

Матрица связности для такой схемы:

 

В этой матрице все связности равны, суммы всех связностей одной строки равны, поэтому данную матрицу можно считать оптимальной. Схему, которой соответствует данная матрица, также можно считать оптимальной.

 

 

Задание №6

Рассчитать методом Якобеуса и методом эффективной доступности требуемое число линий в направлении двухзвенной ступени группового искания, состоящей из g блоков типа 80х120х400.

В рассматриваемом направлении интенсивность поступающей нагрузки равна . Нагрузка на всю ступень ГИ составляет . Доступность в направлении равна . Вероятность потерь .

Сравнить полученные результаты.

Определить способ включения линий.

Построить схему ступени ГИ и схему равномерного неполнодоступного включения линий.

 

Исходные данные:

 

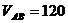линий

линий

линий

линий

блоков

Эрл

Эрл

Решение:

 

Количество выходов коммутатора звена A:

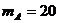
Тогда количество коммутаторов звена А:

.

При связности равной 1:

.

Количество входов в каждом коммутаторе звена B:

.

Количество выходов из каждого коммутатора звена В:

.

Количество коммутаторов звена В:

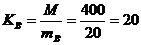
Количество линий из каждого коммутатора в заданном направлении:

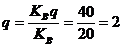
Количество входов в коммутатор звена А:

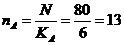, т. е. 4 коммутатора имеют по 13 входов и 2 – по 14.

При построении данной ступени ГИ в каждом направлении в каждом блоке отводится по 40 линий. Всего блоков 10. Если оставить выходы ступени всех блоков незапараллеленными, то всего в каждом направлении получится 10х40=400 линий, а вся ступень распадется на 10 отдельных полнодоступных схем. Если все выходы всех блоков в данном направлении запараллелить, то получим всего одну полнодоступную схему с 40 линиями на направление. В первом случае возрастает расход на оборудование последующих ступеней, причем неоправданно, т. к. нагрузка в направлении существенно меньше количества отведенных линий, во втором случае возрастают потери, т. к. линий слишком мало. Значит необходимо выбрать количество линий в направлении из диапазона 40 – 400, исходя из заданных интенсивности поступающей нагрузки и вероятности потерь.

Найдем требуемое количество линий методом Якобеуса.

Решаем систему уравнений относительно 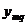и .

 

,

 

где m, n, q, f – параметры ступени.

 

- нагрузка, поступающая на один вход ступени.

- нагрузка, поступающая на всю ступень ГИ.

- количество входов в одном блоке ступени.

- количество блоков.

 

Получаем, что

Эрл.

получаем систему:

 

Решая данную систему, получаем для и следующие значения:

 

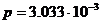
Эрл при вероятности потерь

Эрл при вероятности потерь

 

Далее находим коэффициенты и :

 

 

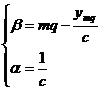
Подставляем найденные значения для интенсивностей нагрузки:

 

.

 

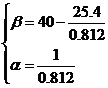
Определяем требующееся количество линий:

 

, где - нагрузка в рассматриваемом направлении ( Эрл).

 

линии.

 

Решим эту же задачу другим методом – методом эффективной доступности.

 

Эффективная доступность определяется из выражения:

 

, где

Эрл.

 

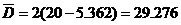
Получаем:

.

По таблице для доступности 27 и вероятности потерь 0.003 определяем коэффициенты и :

 

 

Определяем требующееся количество линий:

 

линии.

 

Из сравнения решений, полученных двумя различными способами, видно, что они отличаются незначительно. Возьмем количество требуемых линий равным 53 линии.

Построим схему неполнодоступного включения линий:

Запараллеливание будем производить цилиндрами.

Учитываем, что при запараллеливании цилиндрами из каждого цилиндра выходит g линий (10 линий). Всего линий требуется 53, но для создания запаса и для удобства построения, возьмем число линий, равным 60.

 

 

Первая строка матрицы связности для первого цилиндра: d 1 1 2 2 0 1 2 1

Первая строка матрицы связности для 2-го и 3-го цилиндров:

D 1 1 1 1 2 1 1 1 1

Первая строка матрицы связности для трех цилиндров: d 3 3 4 4 4 3 4 3 3

Первая строка матрицы связности для всей системы:

d 33 33 34 34 34 33 34 33 33

Значения связностей не отличаются больше, чем на единицу, следовательно, такую систему можно считать оптимальной.

 

Общая матрица связности:

d 33 33 34 34 34 33 34 33 33

33 d 33 33 34 34 34 33 34 33

33 33 d 33 33 34 34 34 33 34

34 33 33 d 33 33 34 34 34 33

33 34 33 33 d 33 33 34 34 34

34 33 34 33 33 d 33 33 34 34

34 34 33 34 33 33 d 33 33 34

34 34 34 33 34 33 33 d 33 33

33 34 34 34 33 34 33 33 d 33

33 33 34 34 34 33 34 33 33 d

Рисунок 18- Схема объединения выходов

 

Задание №7

 

Для четырехзвенной коммутационной системы блочной структуры, работающей в режиме ГИ, определить вероятность потерь методом вероятностных графов.

 

Исходные данные:

 

- число входов в один коммутатор звена А.

- число коммутаторов звена А.

- число коммутаторов звена B.

- количество блоков коммутаторов.

Эрл – интенсивность поступающей нагрузки на один вход коммутатора.

 

Рисунок 19 – Схема коммутатора ступени ГИ

Решение:

 

Построим граф для данной коммутационной схемы:

 

 

Вероятности p1, p2, p3 – вероятности занятия соответствующих ребер графа (п