Лабораторная работа 2.

К. М. Зубрилин

Эконометрика

Лабораторный практикум

Феодосия 2017

 

Содержание

 

 

 

Лабораторная работа 1.

Модель парной регрессии

 

Задание 1. Предприятие имеет большое количество филиалов, и руководство этого предприятия хотело бы знать, как годовой товарооборот одного филиала зависит от торговой площади. Данные приведены в таблице 1.

Необходимо построить линейную регрессионную модель. Для построенной модели определить коэффициент корреляции. Охарактеризуйте тесноту линейной зависимости. Определить коэффициент эластичности.

Таблица 1.

номер филиала	торговая площадь, тыс. кв. м.	годовой товарооборот одного филиала, млн. руб.
	15,72	35,66
	15,75	35,63
	15,76	35,7
	15,78	35,63
	15,81	35,72
	15,82	35,63
	15,84	35,64
	15,87	35,7
	15,88	35,76
	15,9	35,85
	15,93	35,72
	15,94	35,83
	15,96	35,88
	15,99	35,9
		35,87
	16,02	35,88
	16,05	35,84
	16,06	36,01
	16,08	36,03

, .

 

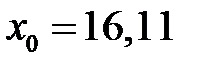Решение

1) Объясняющим фактором 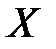будет торговая площадь, тыс. кв. м., а объясняемым фактором – годовой товарооборот одного филиала, млн. руб. Зависимость от ищем как парную линейную регрессионную модель

,

где

,

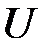– случайная величина (случайный член), характеризующая отклонение от функции регрессии. Эту переменную будем называть возмущением, либо ошибкой,

, ,

, .

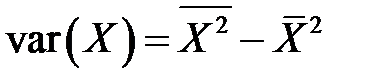Подставляя данные, получаем

, ,

,

.

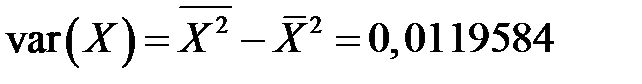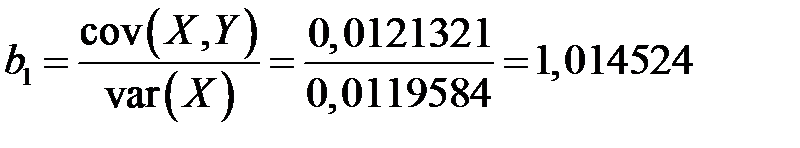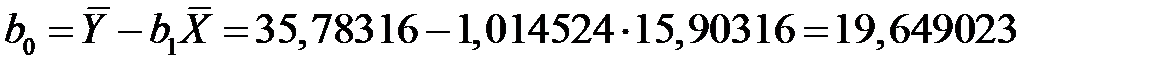Таким образом, уравнение парной линейной регрессии имеет вид

.

 

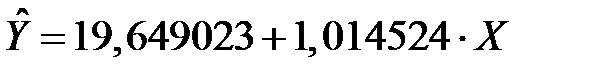2) Коэффициент корреляции находим по формуле

,

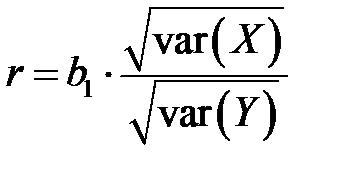где .

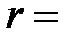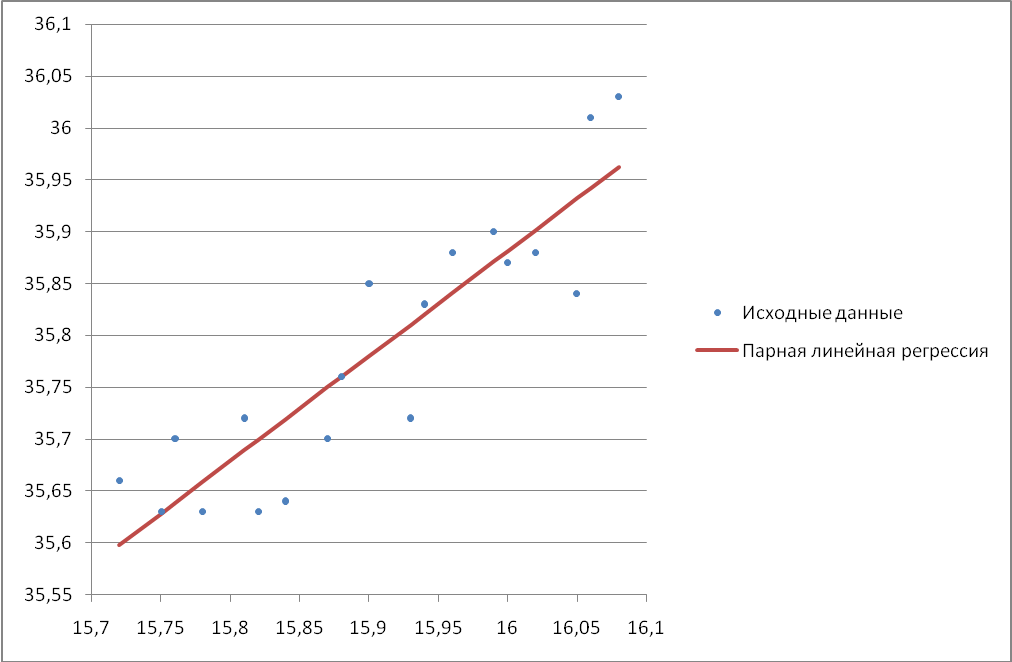
Получили 0,897059. Значит между и 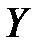сильная корреляционная связь. При этом все наблюдаемые значения вытянуты вдоль прямой линии.

 

 

3) Коэффициент эластичности находим из равенства

.

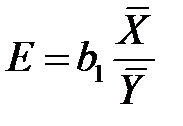Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем зависимая переменная 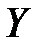при увеличении объясняющей переменной 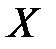на один процент.

0,45.

Таким образом, при увеличении объясняющей переменной 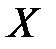на один процент зависимая переменная 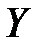в среднем увеличится на 0,45.

 

Вопросы для самопроверки

1. Какая зависимость называется функциональной, статистической и корреляционно?

2. Что называется уравнением регрессии?

3. Что называется функцией регрессии?

4. Когда уравнение регрессии становится выборочным?

5. В чем суть метода наименьших квадратов?

6. Приведите построение линейной парной регрессии?

7. Что является мерой корреляционной связи?

 

 

 

Лабораторная работа 2.

Оценка значимости и адекватности парной регрессионной модели

 

Задание 2. Для доверительной вероятности 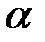найти доверительные интервалы параметров уравнения регрессии. Сделать вывод о значимости коэффициентов линейной регрессии.

Найти коэффициент детерминации. Сделать вывод об адекватности построенной модели априорным данным.

Определить доверительный интервал для дисперсии ошибок.

Для значения 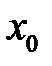признака 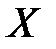найти прогнозное значение зависимого признака . Определить доверительный интервал полученного значения зависимой переменной.

 

Решение

1. Для доверительной вероятности 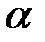найти доверительные интервалы параметров уравнения регрессии. Сделать вывод о значимости коэффициентов линейной регрессии.

Доверительный интервал для параметра имеет вид

,

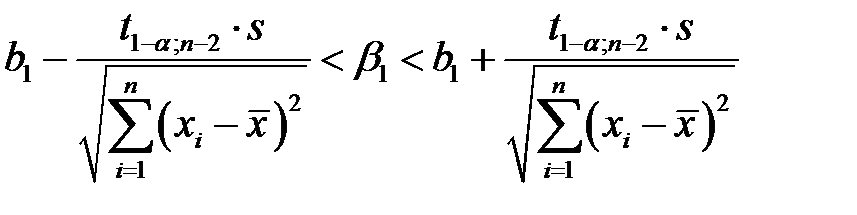где , , 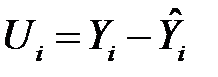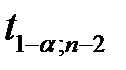– критическое значение распределения Стьюдента для уровня значимост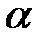и и 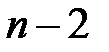степеней свободы (находим по таблице критических точек или с помощью функции EXCEL: СТЬЮДРАСПОБР[1]).

.

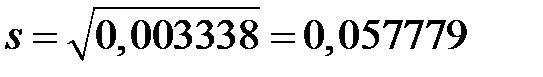С помощью функции СТЬЮДРАСПОБР находим

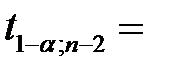СТЬЮДРАСПОБР .

.

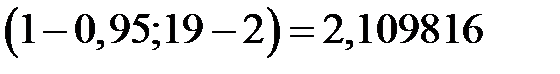Отсюда получаем радиус доверительного интервала

Таким образом, получаем доверительный интервал

.

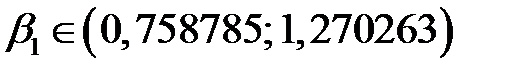Так как 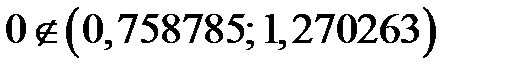, то коэффициент 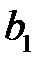является значимым.

Доверительный интервал для параметра имеет вид

.

Находим

,

.

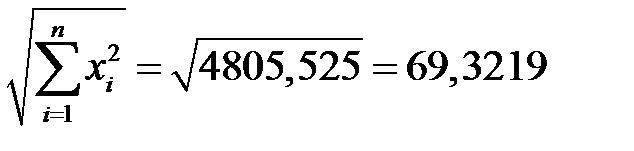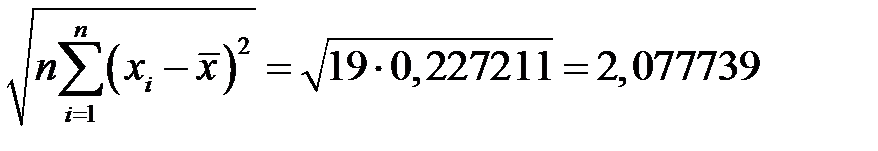Отсюда получаем радиус доверительного интервала

.

Таким образом, получаем доверительный интервал

.

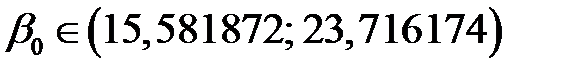Так как , то коэффициент 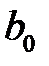является значимым.

 

2. Найти коэффициент детерминации. Сделать вывод об адекватности построенной модели априорным данным.

Коэффициент детерминации определяем по формуле

,

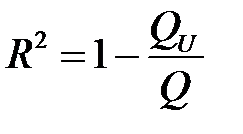где 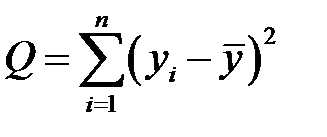, . Подставляя исходные значения, обнаруживаем

, , .

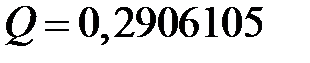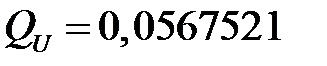Для проверки адекватности построенной модели априорным данным применяем критерий Фишера – Снедекора. Для этого находим наблюдаемое значение 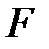-критерия по формуле

,

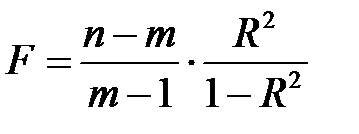где 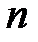– объем выборки, – число параметров уравнения регрессии (в нашем случае ).

По таблице критических точек распределения Фишера – Снедекора или с помощью функции EXCEL: FРАСПОБР[2], определяем критическое значение .

Неравенство 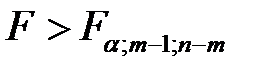является критерием соответствия математической модели, выражающей зависимость между переменными, экспериментальным данным и достаточности включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Подставляя данные, получим

,

.

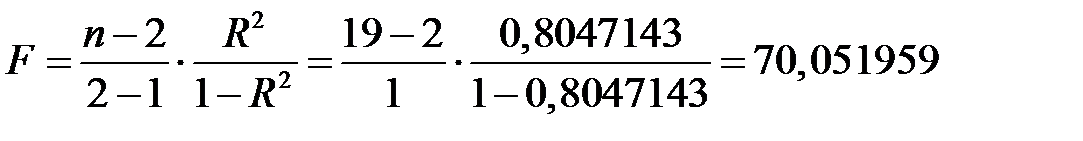Поскольку

,

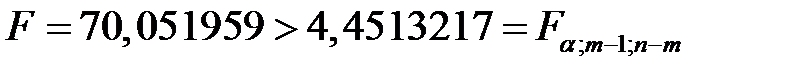то согласно критерию Фишера – Снедекора построенная модель адекватна исходным данным.

 

3. Определить доверительный интервал для дисперсии ошибок.

Доверительный интервал для дисперсии ошибок имеет вид

,

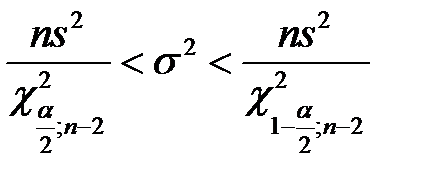где и .

Подставляя данные, получим

.

 

4. Для значения 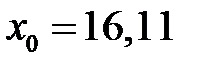признака 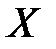найти прогнозное значение зависимого признака . Определить доверительный интервал полученного значения зависимой переменной.

Для нахождения прогнозного значения зависимого признака в уравнение регрессии вместо признака подставляем 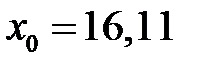, то есть . Получим

.

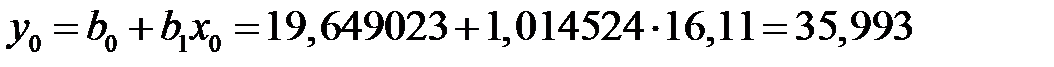Доверительный интервал полученного значения 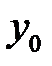имеет вид

.

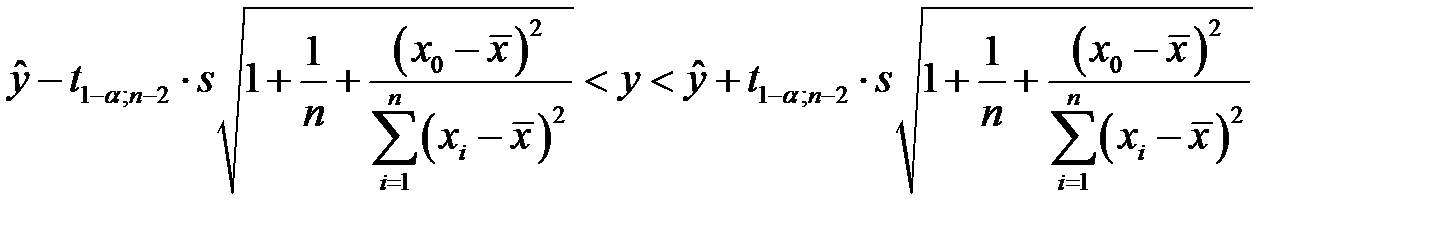Подставляя полученные данные, находим

,

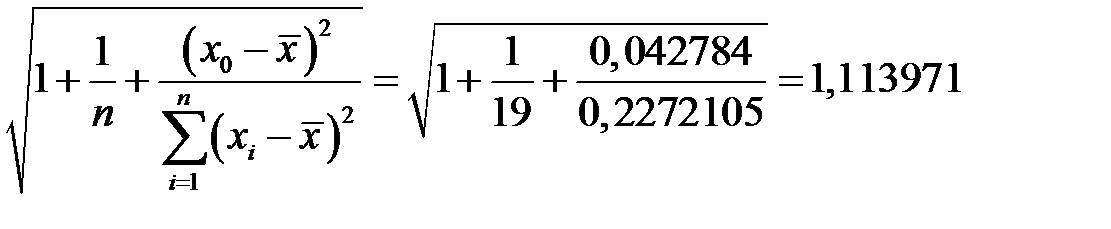Радиус доверительного интервала

.

Отсюда уже получаем доверительный интервал

.

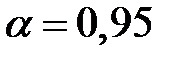Таким образом, интервал с вероятностью накрывает точное значение зависимой переменной .

 

Вопросы для самопроверки

1. Приведите основные положения регрессионного анализа.

2. Как определяются доверительные интервалы для параметров, условного математического ожидания, индивидуальных значений зависимой переменной и дисперсии ошибок?

3. Приведите несмещенные оценки факторной и остаточной дисперсий.

4. Объясните гипотезу о равенстве факторной и остаточной дисперсий.

5. Что называется коэффициентом детерминации?

6. Сформулируйте критерий Фишера – Снедекора.