Алгоритм нахождения корня нелинейного уравнения по методу Ньютона для уравнения с одной переменной

Математическое обоснование

 

Пусть дана вещественная функцияƒ(x) , которая определена и непрерывна на рассматриваемом участке.

Вывод уравнения основано на методе простых итераций, в соответствии с которым уравнениеƒ(x)=0 приводят к эквивалентному уравнению:

(1.10)

при любой функцииλ(x)≠0. Введем понятие сжимающего отображения, которое определяется соотношением:

(1.11)

Для наилучшей сходимости метода в точке очередного приближенияx^ψдолжно выполняться условие:

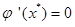(1.12)

Данное требование означает, что корень функции ƒ(x)=0 должен соответствовать экстремуму функции φ(x).

Производная сжимающего отображенияφ(x)определяется в следующем виде:

(1.13)

Выразим из данного выражение переменнуюα(x) при условии принятого ранее утверждения о том, что при ƒ(x)=0 необходимо обеспечить условиеφ`(x^ψ) = 0. В результате получим выражение для определения переменнойα(x):

(1.14)

С учетом этого сжимающая функция прием следующий вид:

(1.15)

Таким образом, алгоритм нахождения численного решения уравненияƒ(x)=0 сводится к итерационной процедуре вычисления:

(1.16)

Алгоритм нахождения корня нелинейного уравнения по методу Ньютона для уравнения с одной переменной

 

1. Задать начальную точку приближенного значения корня функцииx₀ , а также погрешность расчета (малое положительное число ζ ) и начальный шаг итерации (k=0).

2. Выполнить расчет приближенного значения корня функции в соответствии с формулой:

(1.17)

3. Проверяем приближенное значение корня на предмет заданной точности, в случае:

- если разность двух последовательных приближений станет меньше заданной точности

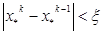(1.18)

то итерационный процесс заканчивается.

- если разность двух последовательных приближений не достигает необходимой точности

(1.19)

то необходимо продолжить итерационный процесс (k=k+1) и перейти к пункту2 рассматриваемого алгоритма.

 

1.3 Метод прямоугольников

 

Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f(x) на интервале интегрирования заменяем полиномом нулевой степени, т.е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая -аппроксимирующая константа. Отсюда происходит и название методов. Как будет показано ниже, из методов прямоугольников наименьшую по­грешность имеет метод средних прямоугольников, когда константу берем равной значению f(x) в средней точке интервала интегрирования [x_j-1, х_j].

 

Рис.1.5 Метод средних прямоуголь­ников

 

 

Рис.1.6 Метод левых прямоугольников

 

Рис.1.7 Метод правых прямоугольников

 

Формула интегрирования для i-го участка для метода левых прямоугольников:

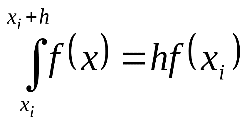(1.20)

Формула интегрирования для метода левых прямоугольников:

(1.21)

Формула интегрирования для i-го участка для метода правых прямоугольников:

(1.22)

Формула интегрирования для метода правых прямоугольников:

(1.23)

Формула интегрирования для i-го участка для метода средних прямоугольников:

(1.25)

Формула интегрирования для метода средних прямоугольников:

(1.26)

Методы левых (рис.1.6) и правых прямоугольников (рис.1.7), заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно высокую погрешность.

Запишем выражение для интеграла на интервале [х_j,х_j+h], полученное методом средних прямоугольников:

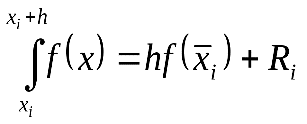(1.27)

Где R_i=J_точн– J_прибл, и оценим погрешность R_i. Для этого разложим подынтегральную функцию f (х) в ряд Тейлора около средней точки :

(1.28) В малой окрестности точки х этот ряд с высокой точностью представляет функцию f(x)при небольшом количестве членов разложения. Поэтому, подставляя под интеграл вместо функции f(x) ее тейлоровское разложение и, интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью:

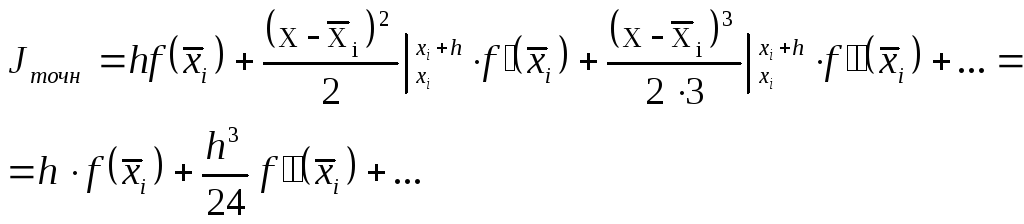(1.29)

При интегрировании и подстановке пределов получаем, что все интегралы от членов ряда, содержащих нечетные степени , обращаются в нуль.

Сравнивая соотношения, можно записать выражение для погрешности R_i.При малой величине шага интегрирования h основной вклад в погрешность R_iбудет вносить первое слагаемое, которое называется главным членом погрешности R_0jвычисления интеграла на интервале [x_j,x_j+h]:

(1.30)

Главный член полной погрешности для интеграла на всем интервале [x₀,х_n] определится путем суммирования погрешностей на каждом частич­ном интервале [x_j,x_j+h]

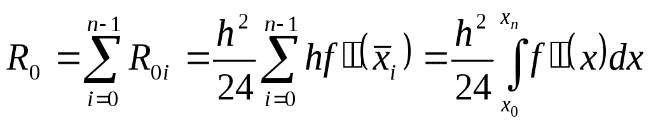(1.31)

К последнему интегралу мы перешли, используя метод левых прямоугольников для функции f"(х).

Формула представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, эта оценка является априорной, так как не требует знания значения вычисляемого интеграла. Степень шага h, которой пропорциональна величина R₀, называется поряд­ком метода интегрирования. Метод средних прямоугольников имеет второй порядок.

Аналогично проведем априорную оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора около точки х=х_j:

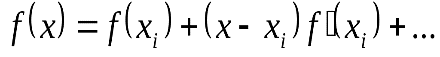(1.32)

Интегрируя разложение почленно на интервале [х_j, х_j+ h], получим:

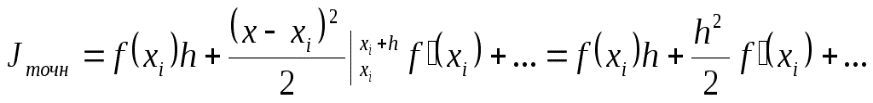(1.33)

где первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников, второе слагаемое является главным членом погрешности:

(1.34)

На интервале [х₀,х_n] главный член погрешности интегрирования полу­чим суммированием частичных погрешностей:

(1.35)

Таким образом, метод левых прямоугольников имеет первый порядок; кроме того, погрешность будет больше по сравнению с методом средних и за счет интеграла от производной f'(x),и коэффициента в знаменателе. Обычно для большинства функций выполняется неравенство:

(1.36)

 

1.4 Метод трапеций

 

В этом методе отрезок [a; b] так же разбивается на n равных частей. На каждом отрезке [x_i; x_i+1] кривая y = f(x) заменяется прямой, проходящей через две известные точки с координатами 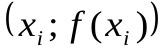и , где и строится прямоугольная трапеция с высотойh(рис. 1.8).

 

 

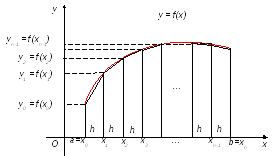
Рис. 1.8 Геометрическая интерпретация метода трапеций

 

В итоге искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических трапеций. Площадь трапеции с высотой h и основаниями a, b вычисляется по формуле:

(1.37)

Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.

Тогда:

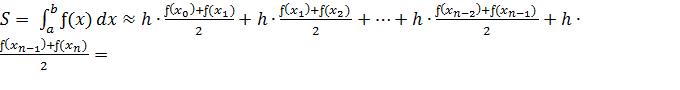(1.38)

вынесем h за скобку, получим:

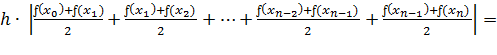(1.39)

разобьем каждую дробь на две дроби:

(1.40)

приведем подобные слагаемые, получим:

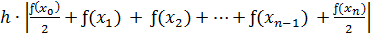(1.41)

Итак :

(1.42)

Коротко полученную формулу можно записать в виде (1.43):

(1.43)

Заметим, что в данном методе получаем ступенчатую фигуру, составленную из трапеций, которая «плотнее» прилегает к заданной криволинейной трапеции, нежели фигура, составленная из прямоугольников в предыдущем методе.

 

 

1.5 Метод Симпсона

 

Значительное повышение точности приближенных формул численного интегрирования дает метод парабол (Симпсона). Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = ƒ(x),чем хорда, соединяющая концы дуги этой кривой (метод трапеций).

 

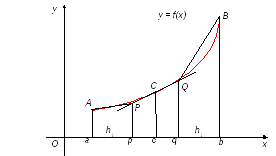
Рис. 1.9 Геометрическая интерпретация метода парабол

 

Поэтому значения площадей соответствующих элементарных трапеций,ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривойy = ƒ(x), чем значения площадей соответствующих прямолинейных трапеций.

Рассмотрим функцию y = f(x). Будем считать, что на отрезке [a; b] она положительна и непрерывна. Найдем площадь криволинейной трапеции aABb (рис 1.9).

Для этого разделим отрезок [a, b] точкой c пополам и в точкеC(c,ƒ(c))проведем касательную к линии y = f(x). После этого разделим [a, b] точками p и q на три равные части и проведем через них прямые x = p и x = q. Пусть P и Q – точки пересечения этих прямых с касательной. Соединив A с P и B с Q, получим три прямолинейные трапеции aAPp, pPQq, qQBb. Тогда площадь трапеции aABb можно приближенно посчитать по следующей формуле:

(1.43)

Где:

(1.44)

Откуда получаем:

(1.45)

Заметим, что aA = ƒ(a), bB = ƒ(b), а pP + qQ = 2ƒ(c) (как средняя линия трапеции), в итоге получаем малую формулу Симпсона

(1.46)

В данном случае дуга ACB заменяется параболой, проходящей через точки A, P, Q, B.

Малая формула Симпсона дает интеграл с хорошей точностью, когда график подынтегральной функции мало изогнут, в случаях же, когда дана более сложная функция, малая формула Симпсона непригодна. Тогда, чтобы посчитать интеграл заданной функции нужно разбить отрезок [a, b] на n частей и к каждому из отрезков применить формулу (1.46).

Обязательным требованием, вытекающим из геометрического смысла метода парабол, является то, что n должно быть четным. Пустьh ,точки деления будут х₀=а, x₁, x₂, …x_n-2, x_n-1, x_n=b; а y₀, y₁, …y_n – соответствующие значения подынтегральной функции на отрезке [a, b].

Тогда, применяя малую формулу Симпсона к каждой паре получившихся отрезков, имеем:

(1.47)

Тогда:

(1.48)

Заметим, что во всех выраженияхI₁,I₂,I_n/2 первый множитель равен h/3:

(1.49)

Сделав замену по формулам (1.49), вынося общий множитель h/3 за скобку, в (1.48) получаем:

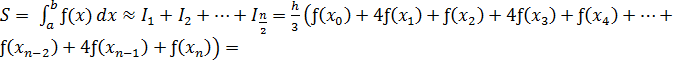(1.50)

Группируем слагаемые:

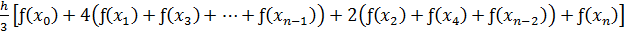(1.51)

Таким образом, получаем «большую» формулу Симпсона, которая имеет вид:

(1.52)

Или по другому можно записать:

(1.52’)

 

2 Блок схемы

Ввод a,b,e

Начало

 

Вычисление F(a)

 

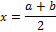
Вычисление F(x)

b=x

 

 

 

F(a) F(x) > 0

Да Нет

 

Нет Да

Выводx

a=x

Конец

 

 

 

Рис. 2.1 Блок-схема метода деления отрезка пополам

 

Началоо

x0,ƒ(x), ƒ’(x)

x=x0

h =

|h|>e

x = x - h

 

Да

_Нет

x

Конец

 

Рис. 2.2 Блок-схема метода Ньютона

Начало

Ввод a,b,n

h = (a-b)/2 s=0

i<n

 

 

Нет

 

Конец

Вывод I

I=h*s

xi=a+i*h s=s+f(xi)

Да

 

Рис. 2.3 Блок-схема метод прямоугольников

 

 

Конец

Вывод I

I = (h/2)*(f(0) + 2*s + f(xn))

xi= a + i*h s = s + f(xi)

i=1; i<n; i++

h=(a-b)/2 s=0

Ввод a, b, n

Начало

 

_Нет

_Да

 

Рис.2.4 Блок-схема метода трапеций

 

 

 

Начало

Ввод a, b, n

h=(a-b)/2 s=0

i=1; i<2*n; i = i+2

j=2; j<2*n; j=j+2

 

^{Нет Нет}

Конец

Вывод I

I = (h/3)*(f(0)+4*s+2*c+f(xn)

xj = a+j*h s = s+f(xj)

xi= a+i*h s = s+f(xi)

Да Да

 

 

Рис. 2.5 Блок-схема метода Симпсона

 

 

3 Используемые программы

 

3.1 Метод деления отрезка пополам

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(const float x){

return 6*x*x-10*x+4;

}

int main()

{

setlocale(LC_ALL,"Russian");

float a, b, x, e1=0.0001, e2=0.001, e3=0.01, e4=0.1;

printf("Введите a=");

scanf("%f", &a);

printf("Введите b=");

scanf("%f", &b);

for(float i=e1; i<=e4; i=i*10)

{

do

{

x=(b+a)/2;

if (f(x)*f(a)>0) a = x;

else b=x;

}

while (b-a>i);

printf("x=%f с погрешностью %f\n", x, i);

}

getch();

}

3.2 МетодНьютона

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(float x)

{

return 6*x*x-10*x+4;

}

floatdf(float x)

{

return12*x-10;

}

 

int main()

setlocale(LC_ALL”Russian”);

{

float e1=0.0001, e2=0.001, e3=0.01, e4=0.1, x, a, b, x0;

printf("Введите a, b и x0 ");

scanf("%f%f%f", &a, &b, &x0);

x=x0-f(x0)/df(x0);

for(float i=e1; i<=e4; i=i*10)

{

while(fabs(x-x0)>i)

{

x0 = x;

x = x - f(x)/df(x);

}

printf("xспогрешностью%f =%f\n", i, x);

}

getch ();

}

 

3.3 Метод прямоугольников

 

Метод левых прямоугольников

 

#include<conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(float x)

{

returnx/(x*x*x*x+3*x*x+2);

}

int main()

{

setlocale(LC_ALL”Russian”);

int n;

float a=1, b=5, h, x1, x, s=0;

printf("Введите n ");

scanf("%d", &n);

h=(b-a)/n;

for (int i=0; i<n; i++)

{

x1=a+i*h;

s=s+f(x1);

}

x=h*s;

printf("Значение интеграла приn = %d = %f\n", n, x);

getch ();

}

 

 

Метод правых прямоугольников

 

#include<conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(float x)

{

returnx/(x*x*x*x+3*x*x+2);

}

int main()

{

setlocale(LC_ALL”Russian”);

int n;

floata=1, b=5, h, x1, x, s=0;

printf("Введите n ");

scanf("%d", &n);

h=(b-a)/n;

for (int i=1; i<=n; i++)

{

x1=a+i*h;

s=s+f(x1);

}

x=h*s;

printf("Значение интегралаn = %d = %f\n", n, x);

getch ();

}

 

 

3.4 Методтрапеций

 

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(float x){

returnx/(x*x*x*x+3*x*x+2);

}

int main()

{

setlocale(LC_ALL”Russian”);

int n;

floata=0, b=1.57, h, x1, s=0, xn, x0, x;

printf("Vvedite n ");

scanf("%d", &n);

h=(b-a)/n;

xn=a+n*h;

x0=a+0*h;

for (int i=1; i<n; i++)

{

x1=a+i*h;

s=s+f(x1);

}

x=(h/2)*(f(x0)+2*s+f(xn));

printf("Znachenieintegralapri n = %d = %f\n", n, x);

getch ();

}

 

3.5 МетодСимпсона

 

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include<clocale>

float f(float x)

{

returnx/(x*x*x*x+3*x*x+2);

}

int main()

{

setlocale(LC_ALL”Russian”);

int n;

floata=0, b=1.57, h, x1, x, s=0, xn, x2, c=0, x0;

printf("Введите n ");

scanf("%d", &n);

h=(b-a)/(2*n);

x0=a+0*h;

xn=a+n*h;

for (int i=1; i<2*n; i=i+2)

{

x1=a+i*h;

s=s+f(x1);

}

for (int j=2; j<2*n; j=j+2)

{

x2=a+j*h;

c=c+f(x2);

}

x=(h/3)*(f(x0)+4*s+2*c+f(xn));

printf("Значениеинтегралапри n = %d = %f\n", n, x);

getch ();

}

 

 

4 Результаты работы

а)

b)

Рис. 4.1 Метод деления отрезка пополам (а – х₁, b – х₂)

а)

 

b)

 

 

Рис. 4.2 Метод Ньютона (а – х₁, b – х₂)

Точные значения корней уравнения 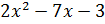равны х₁=-0,386 ;х₂= 3,886.

Таблица 4.1 Вычисленные значения данной функции

	Погрешность для числа разбиения по отношению к точному значению
0,1	0,01	0,001	0,0001
Метод деления отрезка пополам	х1=-0,00008; х2= 0,666664	х1=-0,000015; х2=0,666672	х1=-0,000031; х2=0,666656	х1=-0,000061; х2=0,666687
Метод Ньютона	х1=-0,4; х2=3,9	х1=-0,39; х2=3,88	х1=-0,386; х2=3,886	х1=-0,3860; х2=3,8860

 

 

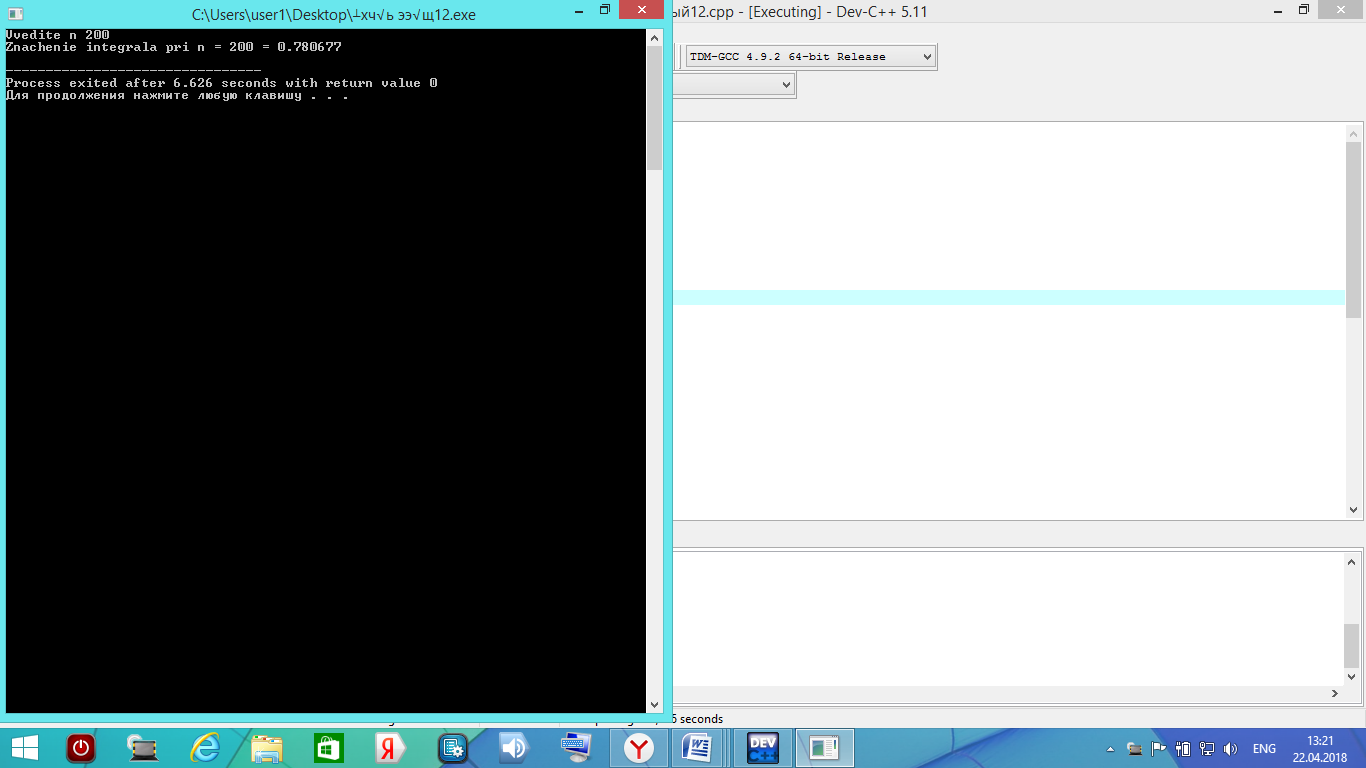
Рис. 4.3 Метод левых прямоугольников

 

Рис. 4.4 Метод правых прямоугольников

 

 

 

Рис. 4.5 Метод трапеции

 

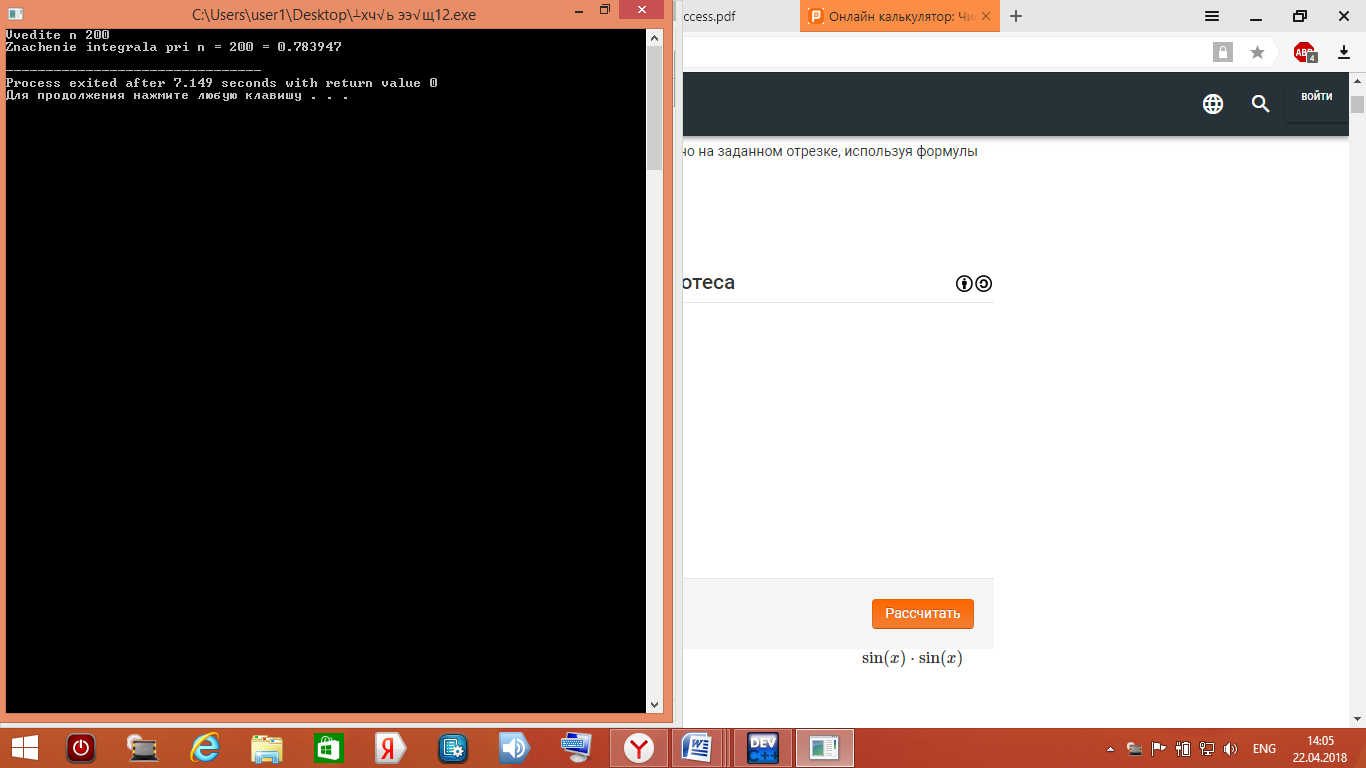
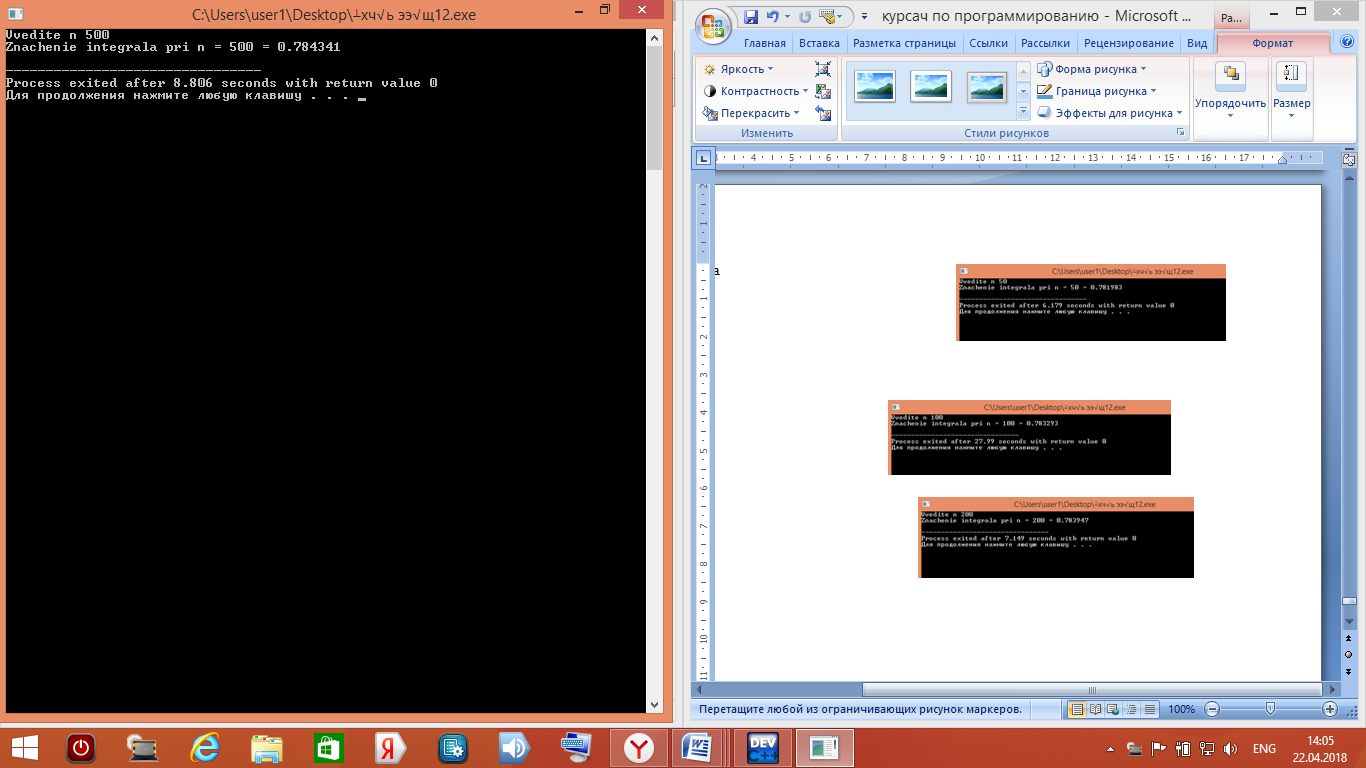
Рис. 4.6 Метод Симпсона

 

Точное значение интеграла sin²(x)равен 0,784

 

Таблица 4.2 Вычисленные значения данного интеграла

	Погрешность для числа разбиения по отношению к точному значению
Метод левых прямоугольников	0,768	0,776	0,780	0,783
Метод правых прямоугольников	0,800	0,792	0,788	0,786
Метод трапеции	0,784	0,784	0,784	0,784
Метод Симпсона	0,781	0,783	0,783	0,784

 

 

ЗАКЛЮЧЕНИЕ

 

Выполняя задание данной курсовой работы, были рассмотрены 2 метода решения уравнений и четыре метода вычисления определённых интегралов. Для рассмотрения этих методов были написаны 6 программ, в каждой из которых были применены знания о языке программирования С++, полученные в процессе прохождения курса информатики.

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1 Пискунов Н.С. Дифференциальное и интегральное исчисление, т. 1: учеб.пособие для вузов / М.: «Наука», 1985. – 432 с.

2 Волков Е. А.. Численные методы: учеб.пособие для вузов. / М.: «Физмалит», 1987. – 248 с.

3 Самарин А.ВОптимизация программ на С++. Проверенные методы повышения производительности: учебное пособие / А.В.Самарин. - Самара : СОЛОН-Р, 2002. - 304 с.

4 Пахомов С. С++ базовый курс: учебник / С.Пахомов. - СПб. : СПбЛТА, 2008. – 244 с.