Пузырьковая сортировка

Алгоритм пузырьковой сортировки [7], общая схема которого представлена в начале данного раздела, в прямом виде достаточно сложен для распараллеливания – сравнение пар значений упорядочиваемого набора данных происходит строго последовательно. В связи с этим для параллельного применения используется не сам этот алгоритм, а его модификация, известная в литературе как метод чет-нечетной перестановки (odd-even transposition) [23]. Суть модификации состоит в том, что в алгоритм сортировки вводятся два разных правила выполнения итераций метода – в зависимости от четности или нечетности номера итерации сортировки для обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется с их правыми соседними элементами. Т.е., на всех нечетных итерациях сравниваются пары

, ,…, (при четном ),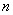

на четных итерациях обрабатываются элементы

, ,…, .

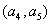После 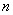-кратного повторения подобных итераций сортировки исходный набор данных оказывается упорядоченным.

Получение параллельного варианта для метода чет-нечетной перестановки уже не представляет каких-либо затруднений – сравнение пар значений на итерациях сортировки любого типа являются независимыми и могут быть выполнены параллельно. Для пояснений такого параллельного способа сортировки в табл. 7.1 приведен пример упорядочения данных при , (т.е. блок значений на каждом процессоре содержит элементов). В первом столбце таблицы приводится номер и тип итерации метода, перечисляются пары процессоров, для которых параллельно выполняются операция "сравнить и разделить"; взаимодействующие пары процессоров выделены в таблице двойной рамкой. Для каждого шага сортировки показано состояние упорядочиваемого набора данных до и после выполнения итерации.

Таблица 7.1. Пример сортировки данных параллельным методом чет-нечетной перестановки

Следует отметить, что в приведенном примере последняя итерация сортировки является избыточной – упорядоченный набор данных был получен уже на третьей итерации алгоритма. В общем случае выполнение параллельного метода может быть прекращено, если в течение каких-либо двух последовательных итераций сортировки состояние упорядочиваемого набора данных не было изменено. Как результат, общее количество итераций может быть сокращено и для фиксации таких моментов необходимо введение некоторого управляющего процессора, который определял бы состояние системы после выполнения каждой итерации сортировки. Однако трудоемкость такой коммуникационной операции (сборка на одном процессоре сообщений от всех процессоров) может оказаться столь значительной, что весь эффект от возможного сокращения итераций сортировки будет поглощен затратами на реализацию операций межпроцессорной передачи данных.

Оценим трудоемкость рассмотренного параллельного метода. Длительность операций передач данных между процессорами полностью определяется физической топологией вычислительной сети. Если логически-соседние процессоры, участвующие в выполнении операций "сравнить и разделить", являются близкими фактически (например, для линейки или кольца эти процессоры имеют прямые линии связи), общая коммуникационная сложность алгоритма пропорциональна количеству упорядочиваемых данных, т.е. . Вычислительная трудоемкость алгоритма определяется выражением

,

где первая часть соотношения учитывает сложность первоначальной сортировки блоков, а вторая величина задает общее количество операций для слияния блоков в ходе исполнения операций "сравнить и разделить" (слияние двух блоков требует операций, всего выполняется 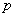итераций сортировки). С учетом данной оценки показатели эффективности параллельного алгоритма имеют вид:

,

(в приведенных соотношениях для величины использовалась оценка трудоемкости для наиболее эффективных последовательных алгоритмов сортировки). Анализ выражений показывает, что если количество процессоров совпадает с числом сортируемых данных (т.е. ), эффективность использования процессоров падает с ростом 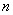; получение асимптотически ненулевого значения показателя 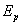может быть обеспечено при количестве процессоров, пропорциональ­ных величине .

Сортировка Шелла

Детальное описание алгоритма Шелла может быть получено, например, в [7]; здесь же отметим только, что общая идея метода состоит в сравнении на начальных стадиях сортировки пар значений, располагаемых достаточно далеко друг от друга в упорядочиваемом наборе данных. Такая модификация метода сортировки позволяет быстро переставлять далекие неупорядоченные пары значений (сортировка таких пар обычно требует большого количества перестановок, если используется сравнение только соседних элементов).

Для алгоритма Шелла может быть предложен параллельный аналог метода, если топология коммуникационный сети имеет структуру -мерного гиперкуба (т.е. количество процессоров равно ). Выполнение сортировки в таком случае может быть разделено на два последовательных этапа. На первом этапе ( итераций) осуществляется взаимодействие процессоров, являющихся соседними в структуре гиперкуба (но эти процессоры могут оказаться далекими при линейной нумерации; для установления соответствия двух систем нумерации процессоров может быть использован, как и ранее, код Грея). Второй этап состоит в реализации обычных итераций параллельного алгоритма чет-нечетной перестановки. Итерации данного этапа выполняются до прекращения фактического изменения сортируемого набора и, тем самым, общее количество таких итераций может быть различным - от 2 до 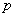. Трудоемкость параллельного варианта алгоритма Шелла определяется выражением:

,

где вторая и третья части соотношения фиксируют вычислительную сложность первого и второго этапов сортировки соответственно. Как можно заметить, эффективность данного параллельного способа сортировки оказывается лучше показателей обычного алгоритма чет-нечетной перестановки при .

Быстрая сортировка

При кратком изложении алгоритм быстрой сортировки (полное описание метода содержится, например, в [23]) основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков существует блок, все значения которого будут меньше значений другого блока). На первой итерации метода осуществляется деление исходного набора данных на первые две части – для организации такого деления выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента, переносятся в первый формируемый блок, все остальные значения образуют второй блок набора. На второй итерации сортировки описанные правила применяются последовательно для обоих сформированных блоков и т.д. После выполнения итераций исходный массив данных оказывается упорядоченным.

Эффективность быстрой сортировки в значительной степени определяется успешностью выбора ведущих элементов при формировании блоков. В худшем случае трудоемкость метода имеет тот же порядок сложности, что и пузырьковая сортировка (т.е. 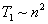). При оптимальном выборе ведущих элементов, когда разделение каждого блока происходит на равные по размеру части, трудоемкость алгоритма совпадает с быстродействием наиболее эффективных способов сортировки ( ). В среднем случае количество операций, выполняемых алгоритмом быстрой сортировки, определяется выражением [7]:

.

Параллельное обобщение алгоритма быстрой сортировки наиболее простым способом может быть получено для вычислительной системы с топологией в виде -мерного гиперкуба (т.е. ). Пусть, как и ранее, исходный набор данных распределен между процессорами блоками одинакового размера 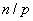; результирующее расположение блоков должно соответствовать нумерации процессоров гиперкуба. Возможный способ выполнения первой итерации параллельного метода при таких условиях может состоять в следующем:

- выбрать каким-либо образом ведущий элемент и разослать его по всем процессорам системы;

- разделить на каждом процессоре имеющийся блок данных на две части с использованием полученного ведущего элемента;

- образовать пары процессоров, для которых битовое представление номеров отличается только в позиции , и осуществить взаимообмен данными между этими процессорами; в результате таких пересылок данных на процессорах, для которых в битовом представлении номера бит позиции равен 0, должны оказаться части блоков со значениями, меньшими ведущего элемента; процессоры с номерами, в которых бит равен 1, должны собрать, соответственно, все значения данных, превышающие значение ведущего элемента.

В результате выполнения такой итерации сортировки исходный набор оказывается разделенным на две части, одна из которых (со значениями меньшими, чем значение ведущего элемента) располагается на процессорах, в битовом представлении номеров которых бит равен 0. Таких процессоров всего и, таким образом, исходный -мерный гиперкуб также оказывается разделенным на два гиперкуба размерности . К этим подгиперкубам, в свою очередь, может быть параллельно применена описанная выше процедура. После -кратного повторения подобных итераций для завершения сортировки достаточно упорядочить блоки данных, получившиеся на каждом отдельном процессоре вычислительной системы. Для пояснения на рис. 7.1 представлен пример упорядочивания данных при 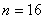, (т.е. блок каждого процессора содержит 4 элемента). На этом рисунке процессоры изображены в виде прямоугольников, внутри которых показано содержимое упорядочиваемых блоков данных; значения блоков приводятся в начале и при завершении каждой итерации сортировки. Взаимодействующие пары процессоров соединены двунаправленными стрелками. Для разделения данных выбирались наилучшие значения ведущих элементов: на первой итерации для всех процессоров использовалось значение 0, на второй итерации для пары процессоров 0, 1 ведущий элемент равен 4, для пары процессоров 2, 3 это значение было принято равным –5.

Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от успешности выбора значений ведущих элементов. Определение общего правила для выбора этих значений не представляется возможным; сложность такого выбора может быть снижена, если выполнить упорядочение локальных блоков процессоров перед началом сортировки и обеспечить однородное распределение сортируемых данных между процессорами вычислительной системы.

Длительность выполняемых операций передачи данных определя­ется операцией рассылки ведущего элемента на каждой итерации сортировки - общее количество межпроцессорных обменов для этой операции на -мерном гиперкубе может быть ограничено оценкой

,

и взаимообменом частей блоков между соседними парами процессоров – общее количество таких передач совпадает с количеством итераций сортировки, т.е. равно 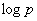, объем передаваемых данных не превышает удвоенного объема процессорного блока, т.е. ограничен величиной .

Вычислительная трудоемкость метода обуславливается сложностью локальной сортировки процессорных блоков, временем выбора ведущих элементов и сложностью разделения блоков, что в целом может быть выражено при помощи соотношения:

(при построении данной оценки предполагалось, что для выбора значения ведущего элемента при упорядоченности процессорных блоков данных достаточно одной операции).

Рис. 7.1. Пример упорядочивания данных параллельным методом быстрой сортировки (без результатов локальной сортировки блоков)

Обработка графов

Математические модели в виде графов широко используются при моделировании разнообразных явлений, процессов и систем. Как результат, многие теоретические и реальные прикладные задачи могут быть решены при помощи тех или иных процедур анализа графовых моделей. Среди множества этих процедур может быть выделен некоторый определенный набортиповых алгоритмов обработки графов. Рассмотрению вопросов теории графов, алгоритмов моделирования, анализа и решения задач на графах посвящено достаточно много различных изданий, в качестве возможного руководства по данной тематике может быть рекомендована работа [8].

Пусть, как и ранее во 2 разделе пособия, 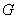есть граф

,

для которого набор вершин 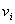, , 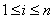задается множеством , а список дуг графа

, ,

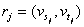определяется множеством 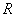. В общем случае дугам графа могут приписываться некоторые числовые характеристики , (взвешенный граф).

Для описания графов известны различные способы задания. При малом количестве дуг в графе (т.е. ) целесообразно использовать для определения графов списки, перечисляющие имеющиеся в графах дуги. Представление достаточно плотных графов, для которых почти все вершины соединены между собой дугами (т.е. ), может быть эффективно обеспечено при помощи матрицы инцидентности

, ,

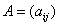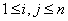ненулевые значения элементов которой соответствуют дугам графа

Использование матрицы инцидентности позволяет использовать также при реализации вычислительных процедур для графов матричные алгоритмы обработки данных.

Далее в пособии обсуждаются параллельные способы решения двух типовых задач на графах – нахождение минимально охватывающих деревьев и поиск кратчайших путей. Для представления графов используется способ задания при помощи матриц инцидентности.