Основные положения расчета оболочек

Основная масса листовых конструкций по расчетной схеме относится к оболочкам и лишь небольшая часть их, например, стенки плоских бункеров, относится к пластинкам. Большинство листовых конструкций имеют те или иные элементы жесткости, ребра, которые с точки зрения расчета представляют собой стержневые системы.

В листовых конструкциях используются тонкостенные осессимметричные сплошные оболочки (оболочки вращения) и пластинки, т.е. их толщина s мала по сравнению с радиусом кривизны r (s/r≤1/30). В основе их расчета лежат гипотезы Кирхгофа и Лява, из которых следует, что напряженное состояние тех и других является двухосным, так как изменения напряжений по толщине малы и ими пренебрегают.

Оболочки отличаются от пластинок наличием кривизны поверхности, определяе­мой гауссовой кривизной I" в каждой точке поверхности (рис.10.1):

I" = (1/r₁)·(1/r₂) , (10.1)

где r₁ и r₂ - главные радиусы кривизны соответственно в меридиональном и кольцевом направлениях для осесимметричных оболочек.

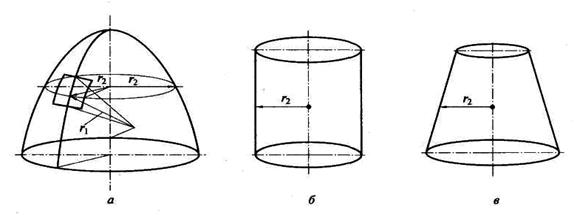
Рис. 10.1. Оболочки вращения: а - эллипсоидальная; б- цилиндрическая; в – коническая

Для листовых конструкций используются оболочки вращения положительной гаycсовой кривизны - сферические и эллипсоидальные (рис. 10.1 а), а также нулевой гауссовой кривизны - цилиндрические и конические, у которых образующей оболочки является прямая линия, т.е. r₁ = ∞ (рис. 10.1 б и в).

В общем случае под действием внешних нагрузок Р воболочках возникают нормаль­ные усилия N₁ и N₂, сдвигающие усилия S₁ и S₂ в плоскостях, касательных к срединной поверхности, изгибающие моменты М₁ и М₂, крутящие моменты М₁₂ и М₂₁ попереч­ные силы Q₁ и Q₂ (рис. 10.2 а). Такое напряженное состояние называется моментным, и ему соответствует моментная теория расчета оболочек, в уравнения которой входят все указанные усилия.

Рис. 10.2. Усилия в элементе оболочки: а - моментное состояние;

б - безмоментное состояние

Если внешняя нагрузка осесимметрична, и оболочка также является осссимметричной и тонкостенной, то в большей ее части имеются только нормальные усилия, а остальными параметрами напряженного состояния ввиду их малости можно пренебречь. При этом напряженное состояние стенки оказывается безмоментным (рис. 10.2 б), и все уравнения существенно упрощаются. Такой подход соответствует безмоментной теории расчета оболочек и может быть применен практически ко всей их поверхности, т.е. там, где отсутствует стеснение свободных радиальных перемещений. В тех местах, где такое стеснение имеет место, необходимо применять моментную теорию расчета; эти зоны называются зонами краевого эффекта. Такие зоны возникают в местах крепления ребер или колец жесткости, в узлах сопряжения оболочек разной гауссовой кривизны, в ме­стах перепада толщины стенки, в зонах краевых закреплений, в местах сосредоточен­ных локальных воздействий (рис. 10.3).

Рис.10.3. Зоны появления краевого эффекта (показаны пунктирной линией)

Таким образом, при расчете тонкостенных оболочек листовых конструкций рас­сматривается как основное безмоментное напряженное состояние, при этом определя­ющими их несущую способность являются нормальные меридиональные и кольцевые напряжения.

То обстоятельство, что оболочки как емкостные конструкции преимущественно работают на осевое растяжение, позволяет наиболее полно использовать несущую спо­собность стали.

Применяя безмоментную теорию расчета оболочек, рассмотрим осесимметричную оболочку двоякой кривизны, нагруженную давлением Р, нормальным к ее срединной поверхности. Для нее после ряда упрощений получено уравнение равновесия Лапласа:

(σ₁/r₁) + (σ₂/r₂) = P/s, (10.2)

где σ₁ и σ₂ - соответственно меридиональные и кольцевые напряжения в оболочке.

Рассмотрим наиболее часто встречающиеся конструктивные формы оболочек.

Для цилиндрической оболочки (рис. 10.4, а) r₁= ∞ и r₂ = const = r, поэтому из уравнения (10.2) можно получить величину кольцевых напряжений:

σ₂ = . (10.3)

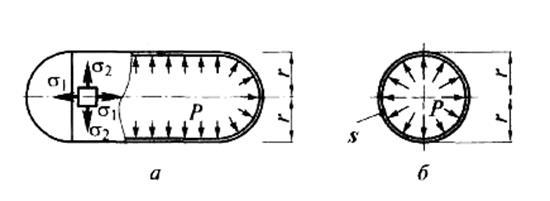
Рис. 10.4. Расчетная схема осесимметричных оболочек,

нагруженных давле­нием Р; а - цилиндрическая оболочка; б - сфе­рическая оболочка

Меридиональные напряжения в ней определяются давлением Р наторцы оболочки. Уравнение равновесия на продольную ось:

Р·π·r² =σ₁2 π·r·s,

откуда

(10.4)

В бесконечно длинных оболочках (при отсутствии днищ) σ₁ = 0. Для сферической оболочки (рис. 10.4 б) имеем r₁ = r₂ = r, поэтому

(10.5)

т.е. меридиональные и кольцевые напряжения в оболочке одинаковы.

При двухосном напряженном состоянии надо проверить приведенное напряжение по четвертой энергетической теории прочности, которое может быть больше, чем каж­дое из значений σ₁ и σ₂: σ_пр = (10.6)

Тонкостенные оболочки всех типов и пластинки при возникновении в них сжимаю­щих напряжений могут потерять устойчивость, т.е. получить мгновенное скачкообраз­ное изменение начальной формы поперечного сечения, или выпучивание. Напряже­ния, при которых это происходит, называются критическими. Напряжения от внешних нагрузок не должны превосходить критические: σ ≤ σ_кр (10.7)

Величина критических напряжений σ_кр зависит от формы оболочки, ее размеров и толщины, от направления действия нагрузок и определяется в каждом конкретном случае для листовых конструкций по СНиП II-23-81 . Формулы, приведенные там, дают относитель­но небольшие значения критических напряжений, потому что в них учтена большая чувствительность тонкостенных крупногабаритных листовых конструкций к начальным дефектам и отступлениям от правильной геометрической формы, а также возможные начальные напряжения и прогибы.