 |
Главная |
Свойства преобразования Лапласа
|
из
5.00
|
Преобразование Лапласа
Оригинал. Показатель роста. Изображение. Свойства преобразования Лапласа. Дифференцирование и интегрирование оригинала. Дифференцирование и интегрирование изображения. Теоремы запаздывания и смещения. Свертка функций. Теорема Бореля. Формула Дюамеля. Операционный метод решения дифференциальных уравнений
Операционное исчисление – это раздел функционального анализа, в котором рассматривается специальный операционный метод решения различных математических задач. Основу этого метода составляет идея интегрального преобразования, переводящего функцию  действительного переменного t в функцию
действительного переменного t в функцию  комплексного переменного р.
комплексного переменного р.
Пусть функция  обладает следующими свойствами:
обладает следующими свойствами:
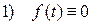 при t <0
при t <0
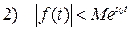 при t >0, где M >0 и
при t >0, где M >0 и  - некоторые действительные постоянные.
- некоторые действительные постоянные.
3) На любом конечном отрезке [а, b] положительной полуоси Ot функция f(t) удовлетворяет условиям Дирихле, т. е.:
а) ограничена;
б) либо непрерывна, либо имеет лишь конечное число точек конечного разрыва
в) имеет конечное число экстремумов.
Такие функции в операционном исчислении называются оригиналами.
Пусть  — комплексный параметр, причем
— комплексный параметр, причем  . При сформулированных условиях интеграл
. При сформулированных условиях интеграл

сходится и является функцией от р:

Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента р называется преобразованием Лапласа от функции  , лапласовым изображением
, лапласовым изображением  ,или просто, изображением
,или просто, изображением  . Тот факт, что функция
. Тот факт, что функция  является изображением оригинала
является изображением оригинала  , обозначают так:
, обозначают так:

В дальнейшем изложении запись 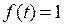 будет означать, что
будет означать, что

Пример 1. Найти изображение оригинала 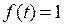
Решение.
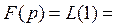
 ~
~ 
 ~
~  ~
~ 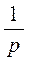
Свойства преобразования Лапласа
1. Однородность. При умножении оригинала на комплексное число изображение также умножается на это число:

Пример 2 . Найти изображение оригинала 
Решение. Используя результат примера 1 и свойство однородности, получаем:

Пример 3. Найти изображение оригинала 
Решение. По определению

 ~
~
~  ~
~
~  ~
~  ~
~
~  ~
~
~  ~
~ 
Пример 4. Найти изображение оригинала 
Решение. По определению

 ~
~ 
2. Аддитивность. Изображение суммы оригиналов равно сумме изображений этих оригиналов:

Пример 5. Найти изображение оригинала 
Решение. Из теории функций комплексного переменного известно, что
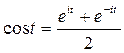
где  - мнимая единица. Следовательно, в силу свойств однородности и аддитивности, а также с учетом примера 4, получаем
- мнимая единица. Следовательно, в силу свойств однородности и аддитивности, а также с учетом примера 4, получаем

3. Подобие. Если  , то справедлива формула:
, то справедлива формула:
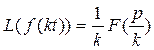
Пример 6. Найти изображение оригинала 
Решение. Воспользуемся результатом примера 5 и свойством подобия:

4. Дифференцирование оригинала. Если  и
и  является оригиналом, то справедлива формула дифференцирования оригинала:
является оригиналом, то справедлива формула дифференцирования оригинала:

где 
Пример 7. Найти изображение оригинала 
Решение. Воспользуемся результатом примера 5 и свойством формулой дифференцирования оригинала:

В общем случае, если  и
и  являются оригиналами, то справедлива формула:
являются оригиналами, то справедлива формула:

где 
5. Интегрирование оригинала. Если  , то справедлива формула:
, то справедлива формула:

Пример 8. Найти изображение оригинала 
Решение. Воспользуемся примером 1 и свойством интегрирования оригинала:

6. Дифференцирование изображения. Если  , то справедлива формула:
, то справедлива формула:

Пример 9. Найти изображение оригинала 
Решение. Воспользуемся примером 8 и свойством дифференцирования изображения:

Таким образом,

7. Интегрирование изображения. Если  и
и  является оригиналом, то справедлива формула:
является оригиналом, то справедлива формула:
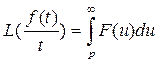
Пример 10. Найти изображение оригинала 
Решение. Из примеров 1, 4 следует, что

Значит, по свойству интегрирования изображения
 ~
~  ~
~
~ 
Итак, 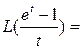

8. Запаздывание. Если  , то справедлива формула:
, то справедлива формула:

Пример 11. Найти изображение оригинала 
Решение. Из примеров 1, 4 следует, что
9. Смещение. Если  , то справедлива формула:
, то справедлива формула:

Пример 12. Найти изображение оригинала 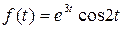
Решение. Из примера 6 следует, что

По условию задачи 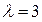 . Следовательно, используя свойство смещения, получаем:
. Следовательно, используя свойство смещения, получаем:
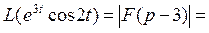

10. Предельные соотношения. Если  и
и 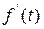 является оригиналом, то справедливы формулы:
является оригиналом, то справедливы формулы:


Свертка функций
Сверткой функций  и
и  называется функция
называется функция

Свойства операции свертывания:
1. коммутативность 
2. ассоциативность 
3. дистрибутивность 
Теорема Бореля. Если  и
и  , то
, то

Другими словами, произведение изображений является изображением свертки их оригиналов
Пример 13. Найти свертку оригиналов 
Решение. Изображения данных оригиналов таковы:

На основании теоремы Бореля получаем


Теорема Дюамеля. Если оригиналы  и
и  непрерывно дифференцируемы на полупрямой [0, ∞), то справедлива формула:
непрерывно дифференцируемы на полупрямой [0, ∞), то справедлива формула:
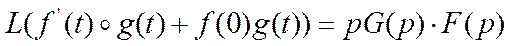
Пример 14. Найти оригинал по изображению 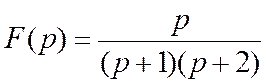
Решение. Из примера 4 следует, что


Пусть  ,
,  ,
,  . Тогда по формуле Дюамеля
. Тогда по формуле Дюамеля



Из примера 13 вытекает, что
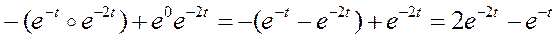
Таблица основных изображений 
| f (t) | F(p) | f (t) | F(p) | ||
| 1 | 1 | 
| 7 | 
| 
|
| 2 | 
| 
| 8 | 
| 
|
| 3 | 
| 
| 9 | 
| 
|
| 4 | 
| 
| 10 | 
| 
|
| 5 | 
| 
| 11 | 
| 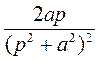
|
| 6 | 
| 
| 12 | 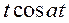
| 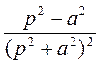
|
|
из
5.00
|
Обсуждение в статье: Свойства преобразования Лапласа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

