Условия независимости криволинейного интеграла 2-го рода от пути интегрирования .

Формула Грина .

Пусть в плоскости 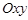 задана замкнутая элементарная относительно оси  или  область , ограниченная замкнутым контуром .

Теорема 2 (формула Грина). Если функции  и  непрерывны вместе со своими частными производными  и  в области , то имеет место формула

,                      (1)

где контур  обходится в положительном направлении.

► Рассмотрим область .

Рис.4.

 

Преобразуем двойной интеграл  к криволинейному интегралу. Имеем

.

Каждый из полученных интегралов равен криволинейному интегралу второго рода, взятому по соответствующей кривой:

,

.

Тогда

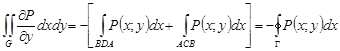. (2)

Аналогично доказывается формула:

.           (3)

При этом область  удобно задать в виде:

.

Вычитая почленно из равенства (3) равенство (2), получим формулу Грина

. ◄

Следствие. Площадь  области , ограниченной контуром , можно вычислить по одной из следующих формул

,          ,            .

► Положим  и . Тогда

.

Аналогично, полагая  и 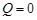, получим .◄

Замечание. 1. Формула Грина справедлива для произвольной области, которую можно разбить на конечное число элементарных областей.

2. Формула Грина связывает интеграл по границе области с интегралом по самой области.

Пример. Вычислить интеграл , где .

Решение. Вычислим интеграл с помощью формулы Грина.

Имеем

, , , .

Тогда

.

 

Условия независимости криволинейного интеграла 2-го рода от пути интегрирования .

Определение 1. Плоская область  называется односвязной, если каков бы ни был замкнутый контур , лежащий внутри этой области, ограниченная этим контуром часть плоскости целиком принадлежит области .

Пример. Односвязными являются круг, эллипс, многоугольник и так далее. Кольцо не является односвязной областью, так как любая окружность, лежащая внутри этой области содержит точки, не принадлежащие этой области.

Теорема 3. Пусть функции  и  определены и непрерывны вместе со своими частными производными  и  в замкнутой односвязной области . Тогда следующие четыре условия эквивалентны:

1) для любой замкнутой кусочно-гладкой кривой , расположенной в , верно

;

2) для любых двух точек  и  области  значение интеграла

не зависит от выбора пути интегрирования , целиком лежащего в ;

3) выражение  представляет собой полный дифференциал некоторой функции, определенной в области :

;

4) в области  всюду .

► Доказательство теоремы проведем по схеме .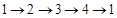

Шаг 1. . Рассмотрим в области  два произвольных пути, соединяющих точки  и , которые в сумме составляют замкнутую кривую , расположенную в .

 

Рис.5.

Рис.6

 

Согласно условию 1 имеем

.

С другой стороны

.

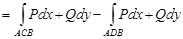Сравнивая, получаем

.

Шаг 2. . Пусть интеграл  не зависит от пути интегрирования, а зависит только от выбора точек  и . Зафиксируем точку .

Тогда интеграл  является некоторой функцией координат  и  точки

.

Покажем, что  дифференцируема в области .

Рассмотрим частное приращение функции  по  в точке

,

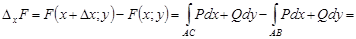
где точка .

Так как интеграл не зависит от вида кривой, то возьмем путь от  до  прямолинейный.

.

Применяя к последнему интегралу теорему о среднем, получаем

, .

Отсюда

, .

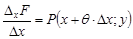Учитывая, что функция  непрерывна, получим

.

Аналогично доказывается, что .

Это означает, что функция  дифференцируема и справедливо равенство .

Шаг 3. . Пусть в области  определена функция  такая, что

.

Тогда

 и .

По теореме о равенстве смешанных производных, имеем:

.

Шаг 4. . Пусть выполнено условие 4) и пусть  – кусочно-гладкая кривая, лежащая в области  и ограничивающая некоторую область . Тогда применяя формулу Грина к области 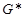, получаем

.

В силу условия 4) интеграл справа равен .

Следовательно, .◄

Замечание. Из эквивалентности условий 1-4 теоремы 2 следует, что условие 4) является необходимым и достаточным условием независимости криволинейного интеграла 1-го рода  от пути интегрирования.

Пример. Вычислить интеграл .

Решение. Здесь 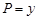, , . Согласно теореме 3, интеграл не зависит от пути интегрирования. Из выполнения условия 4) следует справедливость условия 3). Так как , то

.