 |
Главная |
Лабораторная работа № 3. Парная линейная регрессия
|
из
5.00
|
Цель работы. Освоение построения по выборочным данным модели парной линейной регрессии, оценки точности и надежности параметров и всей модели, построения прогнозов значений зависимой переменной в MS Excel 2010. Интерпретация модели.
Краткие сведения. Модель парной линейной регрессии описывает зависимость условного среднего 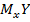 зависимой случайной величины
зависимой случайной величины 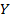 в виде линейной функции значений
в виде линейной функции значений  объясняющей переменной (фактора)
объясняющей переменной (фактора) 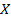 :
:  . Наблюдаемые в выборке
. Наблюдаемые в выборке  значения
значения 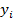 зависимой переменной
зависимой переменной 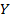 описываются в виде суммы детерминированной
описываются в виде суммы детерминированной  и случайной
и случайной  составляющих:
составляющих:
 . (4)
. (4)
Случайная величина  , называемая ошибкой регрессии, отражает влияние пропущенных объясняющих переменных, неправильной структуры и функциональной спецификации модели, агрегирования переменных, ошибки измерений.
, называемая ошибкой регрессии, отражает влияние пропущенных объясняющих переменных, неправильной структуры и функциональной спецификации модели, агрегирования переменных, ошибки измерений.
Основные предпосылки парной линейной регрессии.
1. Связь значений зависимой величины от значений фактора задается соотношением (4). (Эта зависимость называется спецификацией модели).
2.  – детерминированные величины, линейно не связанные между собой, т.е. векторы
– детерминированные величины, линейно не связанные между собой, т.е. векторы  и (1, 1, …, 1) не коллинеарные.
и (1, 1, …, 1) не коллинеарные.
3. Ошибки регрессии  – случайные величины с
– случайные величины с  для всех
для всех  .
.
4. Ошибки регрессии  и
и  (или переменные
(или переменные 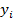 и
и  ) не коррелированы в разных наблюдениях, т.е.
) не коррелированы в разных наблюдениях, т.е.  .
.
5. Ошибки регрессии  распределены по нормальному закону с нулевой средней и дисперсией
распределены по нормальному закону с нулевой средней и дисперсией 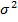 , т.е.
, т.е.  , соответственно
, соответственно  .
.
Модель парной линейной регрессии содержит три неизвестных параметра: коэффициенты 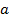 и
и  уравнения регрессии и дисперсию
уравнения регрессии и дисперсию 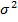 ошибок регрессии
ошибок регрессии  . Оценки коэффициентов
. Оценки коэффициентов 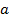 и
и  находятся из условия минимизации по
находятся из условия минимизации по 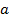 и
и  суммы квадратов
суммы квадратов

отклонений наблюдаемых значений 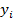 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии  . Эти оценки называются оценками метода наименьших квадратов и определяются соотношениями
. Эти оценки называются оценками метода наименьших квадратов и определяются соотношениями
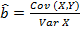 ,
,  ,
,
где  – выборочная ковариация величин
– выборочная ковариация величин 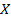 и
и 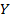 ,
,  – выборочная дисперсия
– выборочная дисперсия 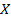 ,
,  и
и  – выборочные средние
– выборочные средние 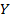 и
и 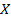 . Согласно теоремы Гаусса-Маркова, при выполнении предпосылок 1 – 4, эти оценки обладают наименьшей дисперсией в классе всех линейных несмещенных оценок. Величины
. Согласно теоремы Гаусса-Маркова, при выполнении предпосылок 1 – 4, эти оценки обладают наименьшей дисперсией в классе всех линейных несмещенных оценок. Величины 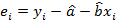 называются остатками регрессии. Несмещенной оценкой дисперсии
называются остатками регрессии. Несмещенной оценкой дисперсии 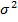 ошибок регрессии
ошибок регрессии  является величина
является величина
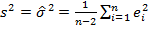 .
.
Оценки дисперсий оценок 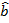 и
и  определяются как
определяются как
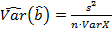 ,
,  .
.
Стандартные отклонения коэффициентов уравнения регрессии определяются соотношениями 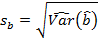 и
и  .
.
Интервальные оценки параметров уравнения регрессии надежности 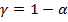 :
:
 ,
,
 ,
,
 (5)
(5)
где  заданный уровень значимости,
заданный уровень значимости,  – квантиль уровня
– квантиль уровня  распределения Стьюдента (
распределения Стьюдента ( 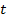 -распределения) с числом степеней свободы
-распределения) с числом степеней свободы  ,
,  и
и  - квантили соответственно уровней
- квантили соответственно уровней  и
и  распределения
распределения 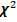 с числом степеней свободы
с числом степеней свободы  .
.
Оцененное уравнение регрессии 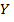 на
на 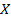 имеет вид
имеет вид 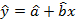 . Статистическая значимость параметров уравнения регрессии (их значимое отличие от нуля) определяется путем проверки принадлежности нулевых значений доверительным интервалам. Если доверительный интервал надежности
. Статистическая значимость параметров уравнения регрессии (их значимое отличие от нуля) определяется путем проверки принадлежности нулевых значений доверительным интервалам. Если доверительный интервал надежности 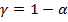 содержит ноль, то нулевая гипотеза о равенстве параметра нулю принимается с уровнем значимости
содержит ноль, то нулевая гипотеза о равенстве параметра нулю принимается с уровнем значимости  . Проверка значимого отличия от нуля параметров
. Проверка значимого отличия от нуля параметров 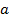 и
и  уравнения регрессии также осуществляется путем проверки нулевых гипотез
уравнения регрессии также осуществляется путем проверки нулевых гипотез  и
и  против альтернативных гипотез
против альтернативных гипотез  и
и 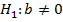 . Для проверки этих гипотез используются
. Для проверки этих гипотез используются 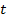 - статистики
- статистики 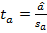 и
и  , распределенные по закону Стьюдента с
, распределенные по закону Стьюдента с 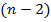 степенями свободы. Если вычисленное значения
степенями свободы. Если вычисленное значения 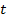 - статистик
- статистик 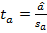 или
или  превышают по модулю критическое значение
превышают по модулю критическое значение  , то нулевая гипотеза отвергается и принимается альтернативная гипотеза (параметр значимо отличается от нуля). Если вычисленное значения
, то нулевая гипотеза отвергается и принимается альтернативная гипотеза (параметр значимо отличается от нуля). Если вычисленное значения 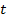 - статистики по модулю меньше критического значения
- статистики по модулю меньше критического значения  , то нулевая гипотеза принимается (параметр незначимо отличается от нуля) при заданном уровне
, то нулевая гипотеза принимается (параметр незначимо отличается от нуля) при заданном уровне  . Критическое значение
. Критическое значение  определяется как квантиль уровня
определяется как квантиль уровня 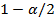 распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  .
.
Верификация и оценка качества модели. Верификация модели парной линейной регрессии означает проверку соответствие модели эмпирическим данным и заключается в установлении значимости уравнения регрессии, т.е. в значимости влияния фактора 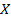 на условную среднюю зависимой величины
на условную среднюю зависимой величины 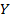 . Проверка значимости уравнения регрессии заключается в проверке нулевой гипотезы
. Проверка значимости уравнения регрессии заключается в проверке нулевой гипотезы  , об отсутствии влияния фактора
, об отсутствии влияния фактора 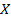 на зависимую величину
на зависимую величину 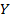 , против альтернативной гипотезы
, против альтернативной гипотезы 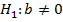 , о значимом влиянии фактора
, о значимом влиянии фактора 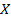 на
на 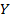 . Значимость уравнения регрессии может быть проверена двумя равноценными способами: с использованием дисперсионного анализа; с использование теории корреляции.
. Значимость уравнения регрессии может быть проверена двумя равноценными способами: с использованием дисперсионного анализа; с использование теории корреляции.
Дисперсионный анализ в линейной регрессии основывается на том, что общая сумма квадратов отклонений 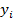 от их общего среднего
от их общего среднего  ,
,  , разлагается на сумму квадратов отклонений объясняемых регрессией,
, разлагается на сумму квадратов отклонений объясняемых регрессией,  , и остаточную сумму квадратов отклонений
, и остаточную сумму квадратов отклонений 
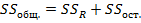 . При справедливости нулевой гипотезы
. При справедливости нулевой гипотезы  средние квадраты
средние квадраты  и
и  являются независимыми несмещенными оценками одной и той же генеральной дисперсии
являются независимыми несмещенными оценками одной и той же генеральной дисперсии 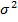 зависимой переменной
зависимой переменной 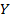 и их различие незначимо. Проверка нулевой гипотезы
и их различие незначимо. Проверка нулевой гипотезы  , при уровне значимости
, при уровне значимости  , сводится к проверке существенности различия несмещенных выборочных оценок
, сводится к проверке существенности различия несмещенных выборочных оценок  и
и  дисперсии
дисперсии 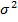 с помощью F- критерия
с помощью F- критерия 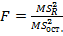 , который имеет F-распределение Фишера-Снедекора с
, который имеет F-распределение Фишера-Снедекора с 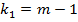 и
и  степенями свободы, где
степенями свободы, где  число коэффициентов в уравнении регрессии. Гипотеза
число коэффициентов в уравнении регрессии. Гипотеза 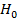 об отсутствии влияния фактора
об отсутствии влияния фактора 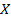 на исследуемый признак
на исследуемый признак 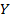 принимается, если вычисленное значение статистики
принимается, если вычисленное значение статистики 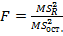 меньше критического
меньше критического 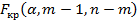 . Если
. Если  , то гипотеза
, то гипотеза  отвергается и принимается гипотеза
отвергается и принимается гипотеза 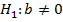 , т.е. фактор
, т.е. фактор 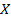 оказывает влияние на исследуемый признак
оказывает влияние на исследуемый признак 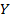 .
.  – квантиль уровня
– квантиль уровня 
 -распределения Фишера-Снедекора с
-распределения Фишера-Снедекора с 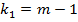 и
и  степенями свободы.
степенями свободы.
Мерой качества уравнения регрессии и характеристикой прогностической силы регрессионной модели является коэффициент детерминации
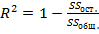 ,
,
который показывает, какая доля вариации зависимой переменной объясняется вариацией фактора.  . Значимое отличие от нуля коэффициента детерминации
. Значимое отличие от нуля коэффициента детерминации  устанавливается также с помощью приведенного выше F- критерия. F- критерий и коэффициент детерминации
устанавливается также с помощью приведенного выше F- критерия. F- критерий и коэффициент детерминации  связаны равенством
связаны равенством 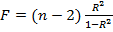 .
.
Использование элементов теории корреляции при проверке значимости уравнения регрессии основано на соотношении 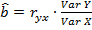 и заключается в проверке значимого отличия от нуля коэффициента корреляции, следовательно, и значимости коэффициента регрессии
и заключается в проверке значимого отличия от нуля коэффициента корреляции, следовательно, и значимости коэффициента регрессии  . Проверка нулевой гипотезы
. Проверка нулевой гипотезы  , т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X, производится с помощью
, т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X, производится с помощью 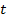 - статистики
- статистики 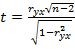 , которая при справедливости нулевой гипотезы имеет распределение Стьюдента (t-распределение) с числом степеней свободы
, которая при справедливости нулевой гипотезы имеет распределение Стьюдента (t-распределение) с числом степеней свободы  . Гипотеза
. Гипотеза  отвергается при уровне значимости
отвергается при уровне значимости  (т.е. уравнение регрессии значимо), если вычисленное по выборке объема
(т.е. уравнение регрессии значимо), если вычисленное по выборке объема  значение
значение 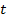 - статистики удовлетворяет неравенству
- статистики удовлетворяет неравенству
 , (6)
, (6)
где  – квантиль уровня
– квантиль уровня 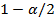 распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  . Если нулевая гипотеза
. Если нулевая гипотеза  принимается, то фактор
принимается, то фактор 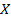 не оказывает влияние на исследуемый признак
не оказывает влияние на исследуемый признак 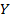 .
.
Для парной линейной регрессии коэффициент детерминации 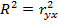 и оба способа проверки значимости уравнения регрессии равнозначны, а F- критерий и
и оба способа проверки значимости уравнения регрессии равнозначны, а F- критерий и 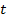 - критерий связаны равенством
- критерий связаны равенством 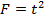 .
.
Прогнозирование по уравнению регрессии. Точечный прогноз 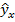 среднего зависимой величины
среднего зависимой величины 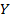 для заданного значения
для заданного значения  вычисляется по уравнению регрессии
вычисляется по уравнению регрессии  и является наилучшей несмещенной линейной оценкой теоретического условного среднего
и является наилучшей несмещенной линейной оценкой теоретического условного среднего  . Доверительный интервал надежности
. Доверительный интервал надежности  прогноза условного среднего для заданного значения
прогноза условного среднего для заданного значения  задается неравенством
задается неравенством
 (7)
(7)
Здесь  – квантиль уровня
– квантиль уровня  распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  ,
, 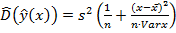 – оценка дисперсии прогноза условного среднего величины Y,
– оценка дисперсии прогноза условного среднего величины Y,  – выборочная дисперсия независимой переменной X. Графики нижней и верхней границ доверительного интервала называются доверительными кривыми надежности
– выборочная дисперсия независимой переменной X. Графики нижней и верхней границ доверительного интервала называются доверительными кривыми надежности  . Уравнение линейной регрессии может быть записано в виде
. Уравнение линейной регрессии может быть записано в виде  . Отсюда следует, что линия регрессии проходит через точку
. Отсюда следует, что линия регрессии проходит через точку 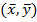 и при
и при 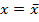 доверительные кривые наиболее близко подходят к линии регрессии.
доверительные кривые наиболее близко подходят к линии регрессии.
Содержание лабораторной работы.
1. Ввести выборочные данные и построить диаграмму рассеяния.
2. Оценить параметры уравнения парной линейной регрессии.
3. Проверить значимость коэффициента корреляции, параметров уравнения регрессии и самого уравнения регрессии при уровне значимости  .
.
4. Оценить точность построенной модели. Построить 95%-й доверительный интервал для дисперсии 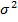 ошибки регрессии.
ошибки регрессии.
5. Построить точечные и интервальные, надежности  , прогнозы среднего зависимой переменной для выборочных значениях независимой переменной. Построить линию регрессии и 95%-е доверительные кривые.
, прогнозы среднего зависимой переменной для выборочных значениях независимой переменной. Построить линию регрессии и 95%-е доверительные кривые.
6. Дать общее заключение об оцененной модели и ее интерпретацию.
Выполнение работы в MS Excel. Выполнение работы в Excel рассмотрим на примере построения регрессионной зависимости  расходов на жилье (y, млрд.дол.) от располагаемого личного дохода (x, млрд.дол.) (функции спроса на жилье в зависимости от располагаемого дохода), используя данные для США за 1959 - 1970 г., приведенные в книге К. Доугерти «Введение в эконометрику». Данные приведены на рис. 4.
расходов на жилье (y, млрд.дол.) от располагаемого личного дохода (x, млрд.дол.) (функции спроса на жилье в зависимости от располагаемого дохода), используя данные для США за 1959 - 1970 г., приведенные в книге К. Доугерти «Введение в эконометрику». Данные приведены на рис. 4.
Ввод данных и построение диаграммы рассеяния . Выборочные данные по расходам на жилье и располагаемому личному доходу разместим по столбцам: в ячейке А1 имя независимой переменной  , в ячейках А2 – А13 ее наблюдаемые значения; в ячейке В1 имя зависимой переменной
, в ячейках А2 – А13 ее наблюдаемые значения; в ячейке В1 имя зависимой переменной  , в ячейках В2 – В13 ее наблюдаемые значения соответствующие значениям независимой переменной.
, в ячейках В2 – В13 ее наблюдаемые значения соответствующие значениям независимой переменной.
Для построения диаграммы рассеяния выберем вкладку «Вставка», в группе «Диаграммы» выберем «Точечная», в ее окне выберем тип диаграммы «Точечная с маркерами». Далее во вкладке «Работа с диаграммами» откроем вкладку «Конструктор» и в группе «Макеты диаграмм» выберем «Макет 1», а в группе «Данные» откроем «Выбрать данные». В открывшемся окне «Выбор источника данных» в поле «Диапазон данных для диаграммы» введем диапазон ячеек с данными для диаграммы, в рассматриваемом примере $A$1:$B$13. Внимание! В первом столбце (строке) должны находится значения независимой переменной. По «ОК» на открытом листе Excel получим диаграмму рассеяния, выделив на ней соответствующие поля введем необходимые названия осей координат и название диаграммы. Диаграмма рассеяния представлена на рис.4.
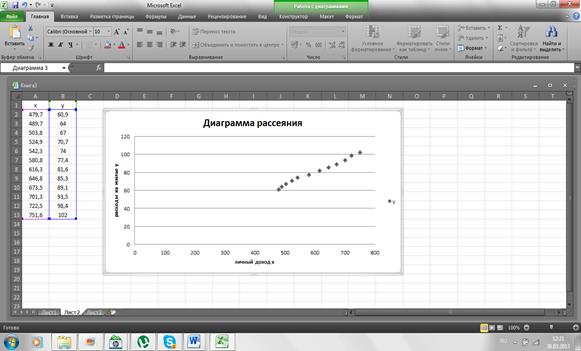
Рис. 4. Данные и диаграмма рассеяния
Оценка уравнения парной линейной регрессии . Откроем вкладку «Данные», в группе «Анализ» выберем надстройку «Анализ данных». В открывшемся окне «Инструменты анализа» выберем функцию «Регрессия». В появившемся окне "Регрессия" укажем входные данные для оценки параметров регрессии, выводимые результаты и их расположение. Заполнение окна "Регрессия" для рассматриваемого примера приведено на рис.5. В части "Входные данные" в поле ввода "Входной интервал Y" указываем диапазон ячеек, содержащий значения зависимой переменной, в нашем примере это B 1: B 13; в поле ввода "Входной интервал X" – диапазон ячеек, содержащий значения независимой переменной, в примере это A 1: A 13. В поле "Метки" устанавливаем флажок  , он указывает на то, что первые строки диапазонов данных содержат имена этих данных (заголовки). В "Константа-ноль" флажок не устанавливаем, в этом случае строится регрессия
, он указывает на то, что первые строки диапазонов данных содержат имена этих данных (заголовки). В "Константа-ноль" флажок не устанавливаем, в этом случае строится регрессия  ; при установке флажка строится регрессия
; при установке флажка строится регрессия  без постоянной
без постоянной 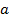 . При установке флажка
. При установке флажка  в левом поле "Уровень надежности", наряду с используемым по умолчанию стандартным уровнем надежности 95% (
в левом поле "Уровень надежности", наряду с используемым по умолчанию стандартным уровнем надежности 95% (  ), можно задать и другое его значение, в этом случае будут выведены интервальные оценки параметров регрессии для двух уровней надежности.
), можно задать и другое его значение, в этом случае будут выведены интервальные оценки параметров регрессии для двух уровней надежности.

Рис. 5. Заполнение окна регрессия
В части "Параметры вывода" указывается одно из мест расположения выводимых результатов:
· "Выходной интервал" – для помещения результатов на текущем рабочем листе, положение результатов указывается заданием верхней левой ячейки, начиная с которой располагаются результаты;
· "Новый рабочий лист" – для расположения результатов на новом рабочем листе;
· "Новая книга" – для помещения результатов в новой книге.
В нашем примере выбран "Выходной интервал" и ячейка А20. Далее, выставляя флажки, указываем какую дополнительную информацию, предлагаемую функцией "Регрессия", мы хотим иметь в результатах:
· "Остатки" – для выдачи прогнозов  и остатков регрессии
и остатков регрессии  ;
;
· "Стандартизованные остатки" – для вывода нормированных остатков  ;
;
· "График нормальной вероятности" – для вывода таблицы, в которой указывается какими персентилями являются наблюдаемые значения зависимой переменной  , и построения соответствующего графика;
, и построения соответствующего графика;
· "График остатков" – для вывода точечной диаграммы остатков  ;
;
· "График подбора" – для вывода наложенных на диаграмму рассеяния точек (  ) линии регрессии
) линии регрессии  .
.
В нашем примере выбраны "Остатки", "График остатков" и "График подбора".
По ОКполучаем результаты регрессии, которые включают в себя таблицу регрессионной статистики, таблицу дисперсионного анализа, таблицу коэффициентов регрессии, таблицу остатков и графики остатков и подбора. Результаты регрессии приведены на рис.6-7. В действительности на экране несколько иная картина, что обусловлено тем, что заголовки некоторых строк и столбцов таблиц не умещаются в ячейках и выводимые графики наложены друг на друга и расположены в правой верхней части экрана. Проведем коррекцию представления полученных результатов.

Рис. 6. Таблицы итогов регрессии.
Прежде всего, отформатируем ячейки содержащие заголовки для получения их полного текста. Для этого, выделив ячейку, щелкнем на ней правой клавишей мышки и в появившемся меню выберем Формат ячейки, затем в окне формата ячейки щелкнем Выравниваниеи в его окне установим флажок в позиции перенос по словам, щелкнув ОК получим полный текст заголовка. Разнесем графики подбора и остатков, разместив их рядом с таблицей остатков.
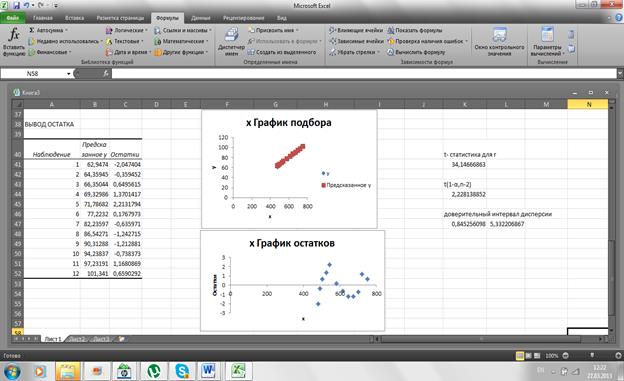
Рис. 7. Остатки и графики результатов регрессии
Пояснения к таблице "Регрессионная статистика":
· Множественный  – множественный коэффициент корреляции между
– множественный коэффициент корреляции между  и
и  ;
;
·  -квадрат – коэффициент детерминации
-квадрат – коэффициент детерминации  ;
;
· Нормированный  -квадрат – скорректированный коэффициент детерминации
-квадрат – скорректированный коэффициент детерминации  , где
, где  число коэффициентов в модели регрессии;
число коэффициентов в модели регрессии;
· Стандартная ошибка – оценка 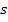 среднеквадратического отклонения
среднеквадратического отклонения 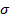 ошибок регрессии
ошибок регрессии  , т.е.
, т.е.  ;
;
· Наблюдений – объем выборки  .
.
Пояснения к таблице "Дисперсионный анализ":
· df – число степеней свободы.
· SS – сумма квадратов.
· MS – средние квадраты.
· F – вычисленное значение критерия Фишера (F-статистики).
· Значимость F – уровень значимости, при котором вычисленное значение критерия Фишера является критической точкой распределения Фишера. Нулевая гипотеза о незначимости уравнения регрессии  отклоняется, если это значение меньше заданного уровня значимости.
отклоняется, если это значение меньше заданного уровня значимости.
· В строке «Регрессия» приведены число степеней свободы равное  , сумма квадратов отклонений
, сумма квадратов отклонений 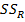 объясняемых регрессией, средний квадрат
объясняемых регрессией, средний квадрат  , значение F и значимость F.
, значение F и значимость F.
· В строке «Остаток» приведены число степеней свободы равное  , остаточная сумма квадратов отклонений
, остаточная сумма квадратов отклонений 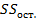 , остаточный средний квадрат
, остаточный средний квадрат 
· В строке «Итого» приведены число степеней свободы  и общая сумма квадратов отклонений
и общая сумма квадратов отклонений  .
.
Следующая таблица содержит МНК-оценки коэффициентов уравнения регрессии, их стандартные ошибки, значения t-статистик для проверки нулевых гипотез  и
и  , P-значения и границы доверительных интервалов для коэффициентов уравнения регрессии для заданных надежностей.
, P-значения и границы доверительных интервалов для коэффициентов уравнения регрессии для заданных надежностей.
В строке с именем "Y-пересечение" приводятся:
· оценка  коэффициента
коэффициента 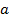 ;
;
· ее стандартная ошибка  ;
;
· вычисленное значение t-статистики, равное  ;
;
· P-значение – вероятность того, что случайная величина распределенная по закону t(n-2) примет значение по абсолютной величине больше, чем модуль вычисленного значения t-статистики, т.е. P-значение это уровень значимости, при котором вычисленное значение t-статистики является критической точкой, следовательно, нулевая гипотеза  отклоняется, если P-значение меньше заданного уровня значимости, и принимается в противном случае;
отклоняется, если P-значение меньше заданного уровня значимости, и принимается в противном случае;
· нижняя и верхняя границы 95%-о доверительного интервала для  .
.
В строке с именем "X" приводятся аналогичные данные для коэффициента  уравнения регрессии.
уравнения регрессии.
Таблица "Вывод остатка" содержит порядковые номера наблюдений  , предсказанные (прогнозные) значения среднего зависимой переменной
, предсказанные (прогнозные) значения среднего зависимой переменной  и остатки регрессии
и остатки регрессии  .
.
На графике подбора выводится диаграмма рассеяния и точки  линии регрессии
линии регрессии  . На графике остатков представлены остатки
. На графике остатков представлены остатки  для наблюдаемых значений
для наблюдаемых значений 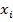 .
.
Таким образом, в рассматриваемом примере выполнив функцию "Регрессия" мы получили:
· уравнение регрессии 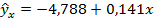 ;
;
· оценку среднеквадратического отклонения ошибок регрессии,  , и оценку дисперсии ошибок
, и оценку дисперсии ошибок  ;
;
· 95%-е доверительные интервалы для коэффициентов уравнения регрессии  и
и  ;
;
· значение t-статистики для коэффициента 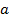 ,
, 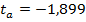 , и ее P-значение, равное
, и ее P-значение, равное  . P-значение больше заданного уровня значимости
. P-значение больше заданного уровня значимости  поэтому принимаем гипотезу
поэтому принимаем гипотезу  , коэффициент
, коэффициент 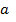 незначимо отличается от нуля.
незначимо отличается от нуля.
· значение t-статистики для коэффициента  ,
,  , и ее P-значение равное
, и ее P-значение равное  , что значительно меньше заданного уровня значимости 0,05, поэтому отклоняем гипотезу
, что значительно меньше заданного уровня значимости 0,05, поэтому отклоняем гипотезу  , следовательно, уравнение регрессии значимо;
, следовательно, уравнение регрессии значимо;
· коэффициент детерминации  вычисленное значение F-статистики,
вычисленное значение F-статистики,  и ее уровень значимости, равный
и ее уровень значимости, равный  , что значительно меньше заданного уровня значимости 0,05, это позволяет отклонить нулевую гипотезу о незначимости коэффициента детерминации
, что значительно меньше заданного уровня значимости 0,05, это позволяет отклонить нулевую гипотезу о незначимости коэффициента детерминации 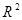 и сделать вывод о значимости уравнения регрессии;
и сделать вывод о значимости уравнения регрессии;
· выборочный коэффициент корреляции, совпадающий со значением "Множественный R" таблицы "Регрессионная статистика", т.е.  ;
;
· прогнозные значения 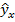 среднего зависимой переменной и остатки регрессии
среднего зависимой переменной и остатки регрессии  для наблюдаемых значений
для наблюдаемых значений  ;
;
· линию регрессии, наложенную на диаграмму рассеяния и график остатков.
Проверка значимости коэффициента корреляции. Проверка значимости коэффициента корреляции, гипотезы  , заключается в проверке неравенства (6). В ячейке В23 находится значение коэффициента корреляции, объем выборки
, заключается в проверке неравенства (6). В ячейке В23 находится значение коэффициента корреляции, объем выборки  . Для вычисления t- статистики
. Для вычисления t- статистики 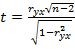 для коэффициента корреляции выделим, например, ячейку К41 и в строке формул введем =В23*(12-2)^0,5/(1-В23^2)^0,5. По «Enter» в ячейке F 10 получим значение t-статистики равное 34,147. Для нахождения критической точки
для коэффициента корреляции выделим, например, ячейку К41 и в строке формул введем =В23*(12-2)^0,5/(1-В23^2)^0,5. По «Enter» в ячейке F 10 получим значение t-статистики равное 34,147. Для нахождения критической точки  распределения Стьюдента при заданном уровне значимости
распределения Стьюдента при заданном уровне значимости  выделим, например, ячейку К44. В вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «СТЬЮДЕНТ.ОБР.2Х». В окне этой функции в поле «Вероятность» введем значение
выделим, например, ячейку К44. В вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «СТЬЮДЕНТ.ОБР.2Х». В окне этой функции в поле «Вероятность» введем значение  , равное 0,05, в поле «Степени свободы» зададим число степеней свободы n-2, равное 10. По «ОК» в ячейке К44 получим значение
, равное 0,05, в поле «Степени свободы» зададим число степеней свободы n-2, равное 10. По «ОК» в ячейке К44 получим значение  , в рассматриваемом примере оно равно 2,228 (см. рис. 7). Модуль t-статистики для коэффициента корреляции превышают критическое значение 2,228, следовательно, коэффициент корреляции значимо отличается от нуля.
, в рассматриваемом примере оно равно 2,228 (см. рис. 7). Модуль t-статистики для коэффициента корреляции превышают критическое значение 2,228, следовательно, коэффициент корреляции значимо отличается от нуля.
Построение 95%-о доверительного интервала для дисперсии  ошибки регрессии . Доверительный интервал надежности
ошибки регрессии . Доверительный интервал надежности 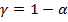 дисперсии
дисперсии 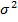 определяется неравенством (5). В примере величина
определяется неравенством (5). В примере величина 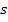 находится в ячейке В26, объем выборки равен 12,
находится в ячейке В26, объем выборки равен 12,  . Функция ХИ2.ОБР находит односторонние критические точки распределения
. Функция ХИ2.ОБР находит односторонние критические точки распределения  при заданном уровне значимости и числе степеней свободы. Для нахождения
при заданном уровне значимости и числе степеней свободы. Для нахождения  выделим ячейку К47 и в строке формул введем = B 26^2*(12-2)/ХИ2.ОБР(0,975;10). По Enter в этой ячейке получим 0,845. Для нахождения
выделим ячейку К47 и в строке формул введем = B 26^2*(12-2)/ХИ2.ОБР(0,975;10). По Enter в этой ячейке получим 0,845. Для нахождения  выделим ячейку L 47 и в строке формул введем = B 26^2*(12-2)/ХИ2.ОБР(0,025;10). По Enter в этой ячейке получим 5,33 (см. рис.7). Следовательно, 95%-й доверительный интервал для
выделим ячейку L 47 и в строке формул введем = B 26^2*(12-2)/ХИ2.ОБР(0,025;10). По Enter в этой ячейке получим 5,33 (см. рис.7). Следовательно, 95%-й доверительный интервал для 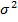 имеет вид
имеет вид  .
.
Построение интервальных прогнозов, надежности  , среднего зависимой переменной для выборочных значений независимой переменной и пос
, среднего зависимой переменной для выборочных значений независимой переменной и пос
|
из
5.00
|
Обсуждение в статье: Лабораторная работа № 3. Парная линейная регрессия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

