 |
Главная |
Образец выполнения кр1
|
из
5.00
|
Задача 1. Дана функция z = cos2(2x – y). Требуется:
1) найти частные производные  и
и  ;
;
2) найти полный дифференциал dz;
3) показать, что для данной функции справедливо равенство:  .
.
Решение.
1) При нахождении  считаем аргумент y постоянным:
считаем аргумент y постоянным:
 = (cos2(2x – y))
= (cos2(2x – y)) 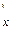 = 2cos(2x – y)(cos(2x – y))
= 2cos(2x – y)(cos(2x – y)) 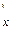 =
=
= 2cos(2x – y)(–sin(2x – y))(2x – y) 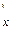 = –2cos(2x – y)sin(2x – y)((2x)
= –2cos(2x – y)sin(2x – y)((2x) 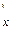 – (y)
– (y) 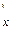 ) =
) =
= – 2cos(2x – y)sin(2x – y)(2 – 0) = –sin(2(2x – y))2 = –2sin(4x – 2y).
При нахождении  считаем аргумент x постоянным:
считаем аргумент x постоянным:
 = (cos2(2x – y))
= (cos2(2x – y))  = 2cos(2x – y)(cos(2x – y))
= 2cos(2x – y)(cos(2x – y))  =
=
=2cos(2x – y)(–sin(2x – y))(2x – y)  = –2cos(2x – y)sin(2x – y)((2x)
= –2cos(2x – y)sin(2x – y)((2x)  – (y)
– (y)  ) =
) =
= – sin(2(2x – y))(0 – 1) = = sin(4x – 2y).
2) По формуле (1) находим полный дифференциал функции:
dz =  = –2sin(4x – 2y)dx + sin(4x – 2y)dy.
= –2sin(4x – 2y)dx + sin(4x – 2y)dy.
3) Найдем смешанные частные производные второго порядка.
Для того чтобы найти  дифференцируем
дифференцируем  по у:
по у:
 =
=  = (–2sin(4x – 2y))
= (–2sin(4x – 2y))  = [считаем x постоянным] =
= [считаем x постоянным] =
= – 2cos(4x – 2y)(4x – 2y)  = – 2cos(4x – 2y)(0 – 2) = 4cos(4x – 2y).
= – 2cos(4x – 2y)(0 – 2) = 4cos(4x – 2y).
Для того чтобы найти 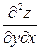 дифференцируем
дифференцируем  по x:
по x:
 =
=  = (sin(4x – 2y))
= (sin(4x – 2y)) 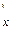 = [считаем y постоянным] =
= [считаем y постоянным] =
= cos(4x – 2y)(4x – 2y) 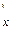 = cos(4x – 2y)(4 – 0) = 4cos(4x – 2y).
= cos(4x – 2y)(4 – 0) = 4cos(4x – 2y).
Получили:  = 4cos(4x – 2y),
= 4cos(4x – 2y),  = 4cos(4x – 2y)
= 4cos(4x – 2y) 
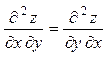 Ответы:
Ответы:
1)  = –2sin(4x – 2y);
= –2sin(4x – 2y);  = sin(4x – 2y);
= sin(4x – 2y);
2) dz = –2sin(4x – 2y)dx + sin(4x – 2y)dy;
3) равенство 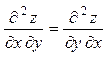 выполнено.
выполнено.
Задача 2. Найти частные производные  ,
,  и
и  , если переменные x, y, и z связаны равенством 4x2 y e z – cos(x3 – z) + 2y2 + 3x = 0.
, если переменные x, y, и z связаны равенством 4x2 y e z – cos(x3 – z) + 2y2 + 3x = 0.
Решение.
Для F(x, y, z ) = 4x2 y e z – cos(x3 – z) + 2y2 + 3x получаем:
F 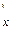 = (4x2 ye z – cos(x3 – z) + 2y2 + 3x)
= (4x2 ye z – cos(x3 – z) + 2y2 + 3x) 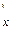 = [считаем y и z постоянными]=
= [считаем y и z постоянными]=
= 8x y e z + sin( x3 – z)3x2 + 3 = 8x y e z + 3x2sin( x3 – z) + 3;
F  = (4x2 y e z – cos(x3 – z) + 2y2 + 3x)
= (4x2 y e z – cos(x3 – z) + 2y2 + 3x)  = [считаем x и z постоянными] =
= [считаем x и z постоянными] =
= 4x2 e z + 4y;
F  = (4x2 y e z – cos(x3 – z) + 2y2 + 3x)
= (4x2 y e z – cos(x3 – z) + 2y2 + 3x)  = [считаем x и y постоянными] =
= [считаем x и y постоянными] =
= 4x2 y e z – sin (x3 – z).
По формулам (2) находим частные производные:
 ;
; 
и по формуле (3) получаем:  .
.
Ответы:  ;
; 
 .
.
Задача 3. Дана сложная функция z = ln(2t – x2y), где  ,
,  . Найти полную производную
. Найти полную производную  .
.
Решение. Используя формулу (4), получаем:

Подставив в полученный ответ  ,
,  , получим:
, получим:

Ответ:  .
.
Задача 4. Дана функция z = x2 – xy + y2 – 4x + 2y + 5 и уравнения границ замкнутой области D на плоскости X О Y: x = 0, y = –1, x + y = 2. Требуется:
1) найти наибольшее и наименьшее значения функции в области D;
2) сделать чертеж области D в системе координат, указав на нем точки, в которых функция имеет наибольшее и наименьшее значения.
Решение.
1) Для наглядности процесса решения построим областьD в системе координат. Область D представляет собой треугольник, ограниченный прямыми
x = 0, y = –1 и x + y = 2. Обозначим вершины треугольника: A, B, C (рис 1).
Чтобы найти наибольшее и наименьшее значения функции z сначала найдем все стационарные точки функции z = x2 – xy + y2 – 4x + 2y + 5, лежащие внутри области D (если они есть), и вычислим в них значения функции.
Стационарные точки – это точки, в которых все частные производные
1-го порядка равны нулю:

Решаем систему:

Стационарная точка М(2, 0)  (рис.1), но не является внутренней точкой области, поэтому значение функции в этой точке вычислим позже.
(рис.1), но не является внутренней точкой области, поэтому значение функции в этой точке вычислим позже.
Теперь найдем наибольшее и наименьшее значения функции на границе области D. Граница является кусочно-заданной, поэтому будем проводить исследование функции z (x, y) отдельно на каждом участке границы.
а) На границе АВ выполняется x = 0 и функция z является функцией одной переменной:  .
.
Исследуем поведение z (y) по правилам нахождения наибольшего и наименьшего значений функции одной переменной на замкнутом промежутке: 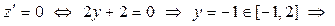 стационарная точка на границе АВ: А(0, – 1);
стационарная точка на границе АВ: А(0, – 1); 
б) На границе АС выполняется у = –1 и функция z является функцией переменной х:

 .
.
Исследуем поведение z (х):  стационарная точка на границе АС: N(1,5, –1);
стационарная точка на границе АС: N(1,5, –1);
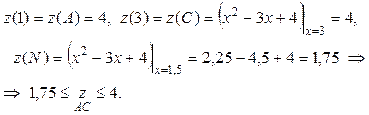
в) На границе ВС выполнено x + y = 2, т.е. y = 2 – х и функция z является функцией одной переменной:

Исследуем поведение z (х):  . Вычислим ординату стационарной точки: y = 2 – x = 0
. Вычислим ординату стационарной точки: y = 2 – x = 0  стационарная точка М(2,0);
стационарная точка М(2,0);
 .
.
Сравнивая все найденные значения функции, выбираем среди них наибольшее и наименьшее значения функции в области D:
 .
.
2) Отметим на построенном ранее чертеже области D (рис. 1) точки, в которых функция имеет наибольшее и наименьшее значения: В(0,2) и М(2,0).
Ответы: 1)  ;
;
2) рисунок 1.
Задача 5. Поверхность σ задана уравнением z =  + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
+ xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Решение.
Найдем частные производные функции z = f (x, y) =  + xy – 5x3:
+ xy – 5x3:
 (x, y) = (
(x, y) = (  + xy – 5x3)
+ xy – 5x3) 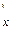 = –
= –  + y – 15x2;
+ y – 15x2;
 (x, y) = (
(x, y) = (  + xy – 5x3)
+ xy – 5x3)  =
=  + x.
+ x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z =  + xy – 5x3
+ xy – 5x3  z0 =
z0 =  + (–1) 2 – 5 (–1)3 = 1.
+ (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
 (М0) = –
(М0) = –  + 2 – 15(–1)2 = –15;
+ 2 – 15(–1)2 = –15;  (М0) =
(М0) =  – 1 = –2.
– 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2)  z – 1= –15x – 15 – 2y +4
z – 1= –15x – 15 – 2y +4  15x + 2y + z + 10 = 0.
15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0:  =
=  =
=  .
.
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали:  =
=  =
=  .
.
|
из
5.00
|
Обсуждение в статье: Образец выполнения кр1 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

