Приведём решение пункта б) без использования пункта а).

Решение.

Чтобы сварить 16 кг вишни, нужно купить 16 1,5 = 24 кг сахара. Значит, нужно купить 24 упаковки сахара.

 

Ответ: 24.

2.На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.

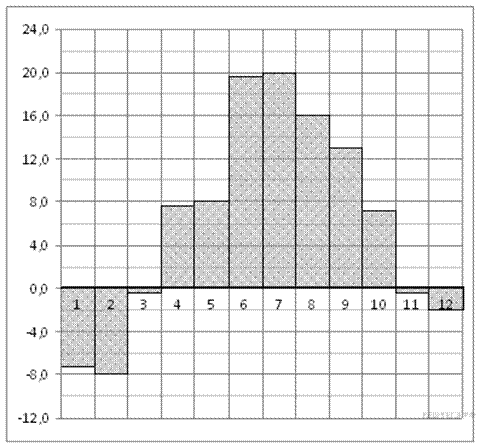
Решение.

Из диаграммы видно, что наименьшая среднемесячная температура во второй половине года составляла −2 °C (см. рисунок).

 

Ответ: −2.

3. На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

Решение.

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Выберем за основание вертикальную сторону, длиной 3 клетки. Тогда проведенная к ней из левой вершины треугольника высота равна 5 клеткам. Поэтому

см².

 

Ответ: 7,5.

4.В слу­чай­ном эксперименте сим­мет­рич­ную монету бро­са­ют трижды. Най­ди­те вероятность того, что вы­па­дет хотя бы две решки.

Решение.

Всего возможных исходов — 8: орел-орел-орел, орел-орел-решка, орел-решка-решка, орел-решка-орел, решка-решка-решка, решка-решка-орел, решка-орел-орел, решка-орел-решка. Благоприятными являются четыре: решка-решка-решка, решка-решка-орел, решка-орел-решка, орел-решка-решка. Следовательно, искомая вероятность равна 4 : 8 = 0,5.

 

Ответ: 0,5.

5.Найдите решение уравнения:

Решение.

Перейдем к одному основанию степени:

 

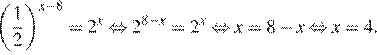
Ответ: 4.

6. В треугольнике ABC угол C равен 90°, , Найдите высоту CH.

Решение.

Поскольку , имеем:

Ответ: 2,4.

7.На рисунке изображен график производной функции определенной на интервале (−4; 13). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −2x − 10 или совпадает с ней.

Решение.

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −2x − 10 или совпадает с ней, их угловые коэффициенты равны –3. Найдем количество точек, в которых y'(x₀) = −2, это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.

 

Ответ: 5.

8.Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.

Решение.

Образующая конуса по теореме Пифагора равна

 

Ответ: 17.

9.Найдите значение выражения

Решение.

Используя свойство степени, имеем:

 

Ответ: 9.

10.Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому , где — мощность излучения звезды (в Ваттах), — постоянная, м — площадь поверхности звезды (в квадратных метрах), а 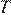— температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна 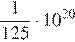м , а мощность её излучения равна Вт. Найдите температуру этой звезды в Кельвинах.

Решение.

Задача сводится к нахождению наименьшего решения неравенства при известном значениях постоянной и заданной площади звезды :

 

 

Ответ: 5000.

11.Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон — 42000 рублей, Гоша — 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.

Решение.

Антон внес уставного капитала. Тогда Борис внес 100 − 12 − 14 − 21 = 53% уставного капитала. Таким образом, от прибыли 1000000 рублей Борису причитается 0,53 · 1 000 000 = 530 000 рублей.

 

Ответ: 530 000.

12.Найдите наименьшее значение функции 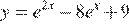на отрезке

Решение.

Найдем производную заданной функции:

Найдем нули производной:

Отметим на рисунке нули производной и поведение функции на заданном отрезке:

Следовательно, наименьшим значением функции на заданном отрезке является ее значение в точке минимума. Найдем его:

 

Ответ: −7.

13.а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Решение.

а) Левая часть уравнения определена, если и При этом

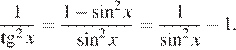
Поэтому уравнение можно переписать в виде

Решив последнее уравнение как квадратное относительно получим или Значит, либо откуда либо что невозможно в силу условия

б) Отберем с помощью единичной окружности отберём корни, принадлежащие промежутку (см. рис.) Получим число

 

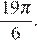
Ответ: а) б)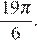

14.В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 6. Найдите расстояние от вершины A до плоскости SBC.

Решение.

Пусть – высота пирамиды. Тогда, так как треугольник равносторонний,

 

Пусть – объём пирамиды, тогда

С другой стороны, где h – искомое расстояние.

В треугольнике 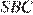высота равна

Площадь треугольник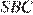а равна Получаем, что

 

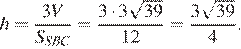
Ответ:

15.Решите неравенство:

Решение.

Решим неравенство системы методом инетервалов:

 

Ответ: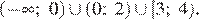

16.В треугольнике ABC точки A₁, B₁ и C₁ — середины сторон BC, AC и AB соответственно, AH — высота,

а) Докажите, что A_1, B₁, C₁ и H лежат на одной окружности.

б) Найдите A₁H, если

Решение.

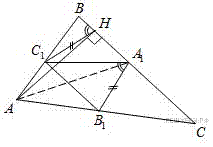
a) Заметим, что — медиана прямоугольного треугольника ABH, значит, но и как средняя линия треугольника АВС. Поэтому четырёхугольник — равнобедренная трапеция, вокруг неё можно описать окружность, а значит, точки и H лежат на одной окружности. Что и требовалось доказать.

б) Середины сторон треугольника являются вершинами подобного ему треугольника. Поэтому верны равенства: Кроме того из п. а) Следовательно,

Пусть R — радиус окружности, описанной вокруг трапеции. Эта окружность одновременно описана вокруг треугольников и Тогда по теореме синусов для каждого из них, имеем:

откуда находим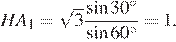

Приведем другое решение пункта а) Так как — медиана прямоугольного треугольника ABH, треугольник равнобедренный, тогда откуда Поскольку сумма противоположных углов четырехугольника равна 180°, а значит, он является вписанным.

Приведём решение пункта б) без использования пункта а).

Найдем сторону АВ треугольника ABC по теореме синусов:

Найдем катет прямоугольного треугольника AHB:

Тогда длина искомого отрезка A₁H:

Замечание. Покажем, что полученная длина равна 1. Действительно, поскольку

имеем:

 

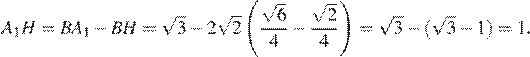
Ответ: б) 1.

17.В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

 

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019
Долг (в млн рублей)	S	0,7S	0,4S

 

Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.

Решение.

Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:

По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:

Следовательно, выплаты с февраля по июнь каждого года составляют:

По условию, разность между наибольшей и наименьшей выплатами должна быть меньше 1 млн рублей:

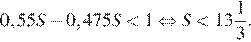
Наибольшее целое решение этого неравенства — число 13. Значит, искомый размер кредита — 13 млн рублей.

 

Ответ: 13.

18.Найдите все значения a, при каждом из которых уравнение имеет хотя бы один корень.

Решение.

Рассмотрим две функции: и Поскольку получаем:

Функция является кусочно-линейной, причём при угловой коэффициент равен либо 3, либо 9, а при угловой коэффициент равен либо –3, либо –9. Значит, функция возрастает при и убывает при поэтому

Исходное уравнение имеет хотя бы один корень тогда и только тогда, когда

Значит, либо

откуда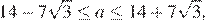

либо

откуда

Исходное уравнение имеет хотя бы один корень при и при и не имеет корней при других значениях

 

Ответ:

19.На доске написано 30 различных натуральных чисел, оканчивающихся на 4 или на 8. Сумма равна 2786.

а) Может ли на доске быть поровну чисел, оканчивающихся на 4 и на 8?

б) Может ли на доске быть ровно 4 числа, оканчивающихся на 8?

в) Каково наименьшее количество чисел, оканчивающихся на 8?

Решение.

а) Если на доске написано по 15 чисел, оканчивающихся на 4 и на 8, то их сумма оканчивается на 0. Это противоречит тому, что сумма 2786.

б) Пусть на доске ровно 4 числа, оканчивающихся на 8. Тогда на доске написано 26 чисел, оканчивающихся на 4. Их сумма не меньше, чем сумма: 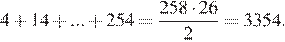Это противоречит тому, что сумма равна 2786.

в) Пусть на доске написано n чисел, оканчивающихся на 8, и 30 − n чисел, оканчивающихся на 4. Тогда сумма чисел, оканчивающихся на 4 не меньше суммы:

Сумма чисел оканчивающихся на 8, не меньше суммы:

Таким образом, откуда n ≤ 8, так как

Если на доске написано 8 чисел, оканчивающихся на 8, и 22 числа, оканчивающихся на 4, то их сумма оканчивается на 2. Значит, чисел, оканчивающихся на 8, больше 8.

Приведём пример 9 чисел, оканчивающихся на 8, и 21 число, оканчивающееся на 4, с суммой 2786: 8, 18, ..., 78, 258; 4, 14, ..., 204.

 

Ответ: а) нет; б) нет; в) 9.

Ключ