МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ

Исследование методов оптимизации

 

Харьков 2009

РЕФЕРАТ

 

Данная курсовая работа содержит : 41 страницу, 16 таблиц, 6 графиков.

В курсовой работе рассмотрены теоретические основы двух методов оптимизации математического программирования :

- метод Нелдера-Мида ;

- градиентный метод с дроблением шага.

Произведена минимизация исследуемой функции указанными методами. Выявлена зависимость числа итераций от заданной точности. Сопоставлена трудоемкость и эффективность оптимизации заданной функции различными методами (градиентным и методом Нелдера-Мида).

Ключевые термины:

Градиент – вектор первых частных производных функции.

Линии уровня – множества точек, в которых функция  принимает постоянные значения, т.е.

Методы нулевого порядка – методы, которые не предполагают вычисления производной для поиска оптимума.

Методы первого порядка – методы, в которых кроме вычисления функции в любой точке предлагается вычисление первых производных.

СОДЕРЖАНИЕ

 

1. Введение

2. Математическое описание методов оптимизации

2.1 Метод Нелдера-Мида

2.2 Градиентный метод с дроблением шага

3. Решение задачи минимизации для каждого из методов

3.1 Метод Нелдера-Мида

3.2 Градиентный метод с дроблением шага

4. Графическая интерпретация решения задачи

5. Аналитическое исследование методов

6. Заключение

7. Приложение

8. Список литературы

СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ

 

 - точка

 - длинна шага

- вектор градиент

E - точность

N – количество итераций

Д – матрица координат симплекса

t – длинна ребра симплекса

ВВЕДЕНИЕ

 

Объектом исследования предмета математическое программирование являются задачи оптимизации.

Оптимизация подразумевает нахождение наилучшего варианта среди всех существующих. В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура должна быть реализована на практике, что во многих реальных случаях вынуждает использовать ЭВМ для выполнения большого объема вычислений.

Универсальных методов, подходящих для поиска экстремума абсолютно любой функции не существует. Данная курсовая работа ставит себе целью исследовать метод оптимизации нулевого порядка – метод Нелдера-Мида, а также метод оптимизации первого порядка – градиентный метод с дроблением шага на примере конкретной функции. Таким образом, получив практические результаты, можно будет сравнить эффективность рассматриваемых методов, применяемых к исследуемой функции.

ПОСТАНОВКА ЗАДАЧИ ( Вариант задания 1)

Исследовать функцию типа :

 

 

Используемые методы минимизации  :

1. Метод: Нелдера-Мида.

2. Метод: Градиентный с дроблением шага.

Необходимо :

1. Решить задачу минимизации , начав итерации из выбранной начальной точки x0=(1;1) заданными по варианту методами, необходимая точность решения . Привести таблицу результатов расчета типа: Итерация: 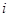 - точка: значение: критерий: .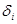

2. Рассчитать 3 линии уровня функции и изобразить их на графике.

3. Отобразить на графиках линий уровня для каждого из заданных методов траекторию движения по итерациям (траекторию спуска).

4. Выявить зависимость числа итераций N от заданной точности E, значения точности: , , , , , . Привести таблицу результатов как в п.1 для каждого значения E.

5. Сравнить эффективность рассмотренных в варианте методов по числу итераций N, построить графики N=F(E).

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ

Метод Нелдера-Мида

 

Вводится симплекс, координаты вершин которого заданы таблицей (одна из вершин в начале координат).

 

 

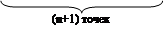
t – некоторое выбранное число.

Если n = 2, то при t = 1 имеем

 

 

Расположение симплекса показано на рисунке 2.1

 

 

Рисунок 2.1- Начальное расположение симплекса

Легко убедиться в том, что если координаты вершин симплекса задать в соответствии с матрицей Д₀ , то расстояние между двумя любыми вершинами симплекса всегда будет равно выбранной константе t независимо от размерности задачи n .

Действительно, расстояние между любой вершиной x_j , j= 2,3,.., n+1, и вершиной x₁ равно

 

 

С другой стороны, расстояние между любой парой вершин  ,  , , 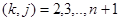равно  Зададим начальную точку процедуры поиска минимума вектором  Перенесем исходный симплекс таким образом, чтобы вершина, находившаяся в начале координат, оказалась в точке . Получим матрицу

 

 

Вычислим значения оптимизируемой функции в точках  и переномеруем точки так, чтобы выполнялись неравенства :

 

.

 

Найдем координаты центра тяжести фигуры , получающейся в результате удаления вершины  :

 

 

Осуществим отражение вершины  относительно центра тяжести. Получим точку

 

.

 

Если a=1 , то получим зеркальное отражение. В одномерном случае процедура отражения, обеспечивающая получение точки  , симметричной точке  относительно  иллюстрируется рис. 2.2

 

 

 

Рисунок 2.2 - Построение точки

 

Сравним теперь между собой значения

Возможны следующие варианты

а) . В этом случае выполняется растяжение симплекса и отыскивается точка

Параметр  обычно принимается равным 1,5.

Полученная точка  заменяет , если . В противном случае для замены  используется точка .

б) . При этом реализуется отражение. Точка  заменяет .

в) 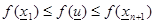. В этом случае осуществляется сжатие и отыскивается точка

Параметр  обычно принимается равным 0,5. Точка  заменяет .

г) . При этом осуществляется редукция (уменьшение размера симплекса путем приближения всех его вершин к вершине 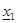). Координаты вершин нового симплекса рассчитываются по формулам

 

 

Критерий останова вычислительной процедуры имеет вид :

 

 

Критерий останова J является составным. При этом его компоненты имеют различный вес в зависимости от того, каков характер поведения оптимизируемой функции в окрестности экстремума. Если в районе экстремума оптимизируемая функция изменяется по типу «глубокая впадина», то больший вклад в численное значение критерия J вносит первое слагаемое, а второе при этом быстро уменьшается. Напротив, если оптимизируемая функция изменяется по типу «пологое плато», то первое слагаемое быстро становится малым и поэтому второе слагаемое вносит больший вклад в величину критерия J.

Модификация метода

Описанный «классический» вариант построения алгоритма метода Нелдера-Мида обладает конструктивным недостатком, который состоит в следующем. Предположим, что оптимизируемая функция, для простоты, двух переменных имеет вид глубокого оврага с очень пологим дном. Тогда может случиться так, что симплекс, который в рассматриваемом случае представляет собой треугольник, в какой-то момент двумя вершинами ляжет на дно оврага, а третья окажется на его склоне. При этом на очередном шаге произойдет переброс этой вершины на другой склон, а затем редукция или сжатие симплекса. Если склон оврага крутой, то эта процедура повторится много раз, в результате чего симплекс сожмется и может сработать критерий останова, хотя до точки минимума еще может быть очень далеко. Естественное усовершенствование алгоритма состоит в следующем. После срабатывания критерия останова целесообразно построить над центром тяжести сжавшегося симплекса новый, размеры которого соответствуют исходному симплексу. Пусть координаты центра тяжести сжавшегося симплекса образуют вектор

 

 .

 

Найдем теперь координаты точки  такой, что центр тяжести симплекса с длиной ребра, равной t , использующего вершину  в качестве начальной, совпадал бы с . Матрица координат указанного симплекса имеет вид

 

                   (2.1)

 

Координаты центра тяжести этого симплекса образуют вектор

 

 

Теперь координаты точки найдем из равенства = , откуда

 

где

 

Подставляя вычисленные значения  в выражение (2.1) , получим требуемый симплекс, используя который продолжим процедуру поиска минимума. С другой стороны, для продолжения процедуры в качестве начальной точки может быть использован центр тяжести «сжавшегося» симплекса. Возникающее при этом смещение нового симплекса относительно сжавшегося (точки предполагаемого останова) во многих случаях может даже оказаться полезным. Эту процедуру считаем законченной, если после очередного сжатия алгоритм приведет в точку, расстояние от которой до точки предыдущего сжатия  не превосходит некоторого достаточно малого .