ЗАДАЧИ КИНЕМАТИКИ, РЕШАЕМЫЕ ПОСРЕДСТВОМ ЯЗЫКА ПАСКАЛЬ

 

Скорости точек плоской фигуры могут быть определены аналитическими , графическими или же графоаналитическими методами.

Аналитический метод. При аналитическом методе должны быть заданы уравнения движения плоской фигуры (рис.2)

Хo ₁ =f ₁ (t) , Yо ₁ =f ₂ (t) , φ = f ₃ (t) . (1*)

Проекции скорости точки М на неподвижные оси координат определяется равенствами:

V _x =Vо ₁ Х-W _z (Y-Yo ₁ )  (2*)

V _y =Vо ₁ Y + W _z (Х-Хo ₁ )   (3*)

В этих формулах V_x , V_y – искомые проекции скорости точки М на неподвижные оси координат; Vо₁x = Хo₁ , Vо₁y = Yo₁-проекции скорости полюса, начала подвижной системы координат ХY на неподвижные оси координат ; W _z =φ -проекция угловой скорости на ось Z , перпендикулярную к плоскости движения ;ХУ координаты точки М в неподвижной системе координат ; Хо₁ ,Yо₁ – координаты полюса О₁ в неподвижной системе осей. Определение координат Х ,Y точки М , по заданным уравнениям движения плоской фигуры (1*) производится по формулам:

Х=Хо₁+Х₁ cosφ – Y₁sin φ

Y= Y о₁+ Х₁ sin φ +Y₁ cos φ

Проекции скорости точки М на неподвижные оси координат находятся по формулам:

Vx₁ =Vo₁ x cos φ + Vo₁ у sin φ – Wzy₁ (4*)

Vу ₁= -Vo₁ x sin φ + Vo₁ у сos φ – Wz х₁ (5*)

В этих формулах Vx , Vу- искомые проекции скорости точки М на оси х, у подвижной системы координат , жестко связанной с плоской фигурой ; х у – координаты точки М в подвижной системе осей , остальные величины имеют то же значение , что и в уравнениях (2*) , (3*).

Величины скорости точки М по известным проекциям определяются формулой:

V= √ Vx ²+ Vу² = √ Vx₁² + Vу₁²   (6*)

Направляющие косинусы даются равенствами:

cos (V,X)= Vx/V , cos (V, У )= Vy/V (7*)

cos (V,X)= Vx/V , cos (V, У )= Vy/V    (8*)

Графоаналитические методы. Первый графоаналитический способ определения скоростей точек плоской фигуры основан на формуле распределения скоростей (рис.2).

 

 

 

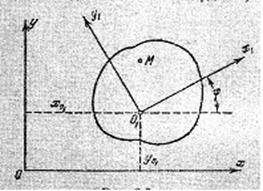
Рис. 2. Геометрическая модель плоской фигуры

V=Vo₁+W r , (9*)

в этой формуле

V – искомая скорости точки М;

Vo₁ - скорость полюса О,

W - угловая скорость плоской фигуры;

r - радиус-вектор , проведенный из полюса О в Рис. 3 точку М.   

Таким образом, зная скорость какой-либо точки плоской фигуры, выбираем эту точку за полюс. Далее откладываем от точки М, скорость которой подлежит определению, вектор, равный скорости полюса, и вектор W r₁, направлен перпендикулярно к r₁, и равный по величине W r₁.Векторная сумма этих слагаемых и дает искомую скорость точки М, Если скорость точки М известна по направлению, то можно не знать величины вращательной скорости W r₁, так как и эта скорость, и искомая скорость точки М определяется пересечением прямой, совпадающей с направлением скорости точки М, и прямой, перпендикулярной к линии О М, проведенной из конца вектора Vо, отложенного из точки М.

После того, как треугольник или параллелограмм скоростей выражающий равенство (9*), построен, задача может считаться решенной. Величина и направление скорости точки М могут быть найдены по рис.(2) или получены из решения этого треугольника.

Формула распределения скоростей (9*)записывается часто в виде:

V_b=V_a+V_ba (9**)

где V-искомая скорость точки В, V _a-известная скорость точки А , избранной за полюс, а

V_ba= W АВ , V_ba = W AB, (9***)

- вращательная скорость точки В вокруг точки А, равная по модулю, произведению мгновенной угловой скорости плоской фигуры на расстояние от точки до полюса и направленная перпендикулярно к отрезку прямой ВА в сторону мгновенного вращения фигуры.

Многие задачи могут быть решены при помощи теоремы о равенстве проекции скоростей концов отрезка плоской фигуры на направление отрезка.

Второй графоаналитический метод определения скоростей плоской фигуры основан на использовании мгновенного центра скоростей этой фигуры. При не поступательном движении плоской фигуры (W=0) в каждый данный момент существует точка тела , скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и обычно обозначается через P. Единственным исключением является случай так называемого мгновенно поступательного движения (W=0), который будет рассмотрен отдельно. Выбирая мгновенный центр за полюс, имеем закон распределения скоростей в плоской фигуре.

V=W r ₁, V=W М Р , (10*)

где V-искомая, скорость произвольной точки М; W-угловая скорость плоской фигуры, r₁-радиус-вектор, проведенный из мгновенного центра скоростей в точку М, называемый мгновенным радиусом. Таким образом, скорости всех точек плоской фигуры являются в данный момент вращательными скоростями вокруг мгновенного центра скоростей. Их величина равна произведению величин угловой скорости на модуль мгновенного радиуса, а направлены они перпендикулярно к мгновенному радиусу. Таким образом, величина скоростей точки плоской фигуры пропорциональны величине мгновенных радиусов:

V_b / ВР=V_a / АР=...=W,           (11*)

При графоаналитических методах решения задач рекомендуется такая последовательность действий:

1) Выбрать за полюс ту точку плоской фигуры, направление скорости которой известно;

2) найти другую точку плоской фигуры, направление скорости которой известно;

1) пользуясь формулой распределения скоростей, найти скорость этой точки плоской фигуры;

2) исходя из формулы распределения скоростей определить значение угловой скорости плоской фигуры в данный момент времени;

3) зная угловую скорость фигуры и скорость полюса, найти с помощью формулы распределения скоростей искомые скорости других точек фигуры.

При графоаналитическом методе решения задач может быть применен метод проекции. В этом случае может быть рекомендован следующий порядок решения задач:

· 1. Выбрать за полюс точку плоской фигуры, скорость которой известна;

· 2. Пользуясь формулой распределения скоростей, построить скорость другой точки плоской фигуры, у которой известно направление ее скорости;

· 3. Спроектировать полученный треугольник скоростей на направление прямой, соединяющей обе точки, и найти скорость второй точки;

· 4. Спроектировать треугольник скоростей на направление, перпендикулярное к прямой, соединяющей обе точки, и найти вращательную скорость второй точки по отношению к полюсу;

· 5. Разделив вращательную скорость на расстояние от точки до полюса, найти мгновенную угловую скорость плоской фигуры;

· 6. Зная мгновенную угловую скорость фигуры, можно найти скорости любых точек плоской фигуры, пользуясь формулой распределения скоростей.

Если задача решается при помощи мгновенного центра скоростей, рекомендуется такая последовательность:

1) определить положение мгновенного центра плоской фигуры;

2) найти величину мгновенного радиуса той точки плоской фигуры, скорость которой известна и определить угловую скорость плоской фигуры, разделив величину скорости точки на величину мгновенного радиуса;

3) найти искомые величины скоростей точек плоской фигуры, умножая угловую скорость на мгновенный радиус соответствующей точки или используя.

Теперь рассмотрим конкретную задачу по кинематике.

Задача. Для преобразования периодического возвратно-поступательного движения во вращательное движение в двигателях внутреннего сгорания применяют шатунно-кривошипный механизм, состоящий из кривошипа ОА= r, вращающегося вокруг неподвижной точки О в плоскости рисунка, шатуна АВ= l, шарнирно соединенного с кривошипом, и поршня В, двигающегося по горизонтальным направляющим цилиндра, совпадающим с прямой ОВ.

 

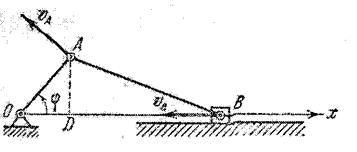
Рис. 3. Геометрическая модель плоского шатунно-кривошипного механизма

 

На основе разработанного алгоритма решения задачи по кинематике составим Паскаль – программу.

Program Kinematika;

Var t,f0,k,b1,b2,x1,x2,a,b,l,d,f1,f2,a1,a2,w1,w:real;

Begin

Write('vvedite welichini a b d l w t = ');

Readln(a,b,d,l,w,t);

x1:=(sqr(d+b)-a*a+l*l)/(2*l*(d+b));

f1:=(180/pi)*arctan(sqrt(1-sqr(x1))/x1);

x2:=(sqr(d+b)-a*a-l*l)/(2*l*a);

a1:=(180/pi)*arctan(sqrt(1-sqr(x2))/x2);

x1:=-(l*l+sqr(d-b)-a*a)/(2*l*(d-b));

f2:=(180/pi)*arctan(sqrt(1-sqr(x1))/x1);

x2:=(l*l-sqr(d-b)+a*a)/(2*l*a);

a2:=(180/pi)*arctan(sqrt(1-sqr(x2))/x2);

f0:=w*t;

k:=sqrt(l*l+b*b-2*l*b*cos(f0));

x1:=(k*k+d*d-a*a)/(2*k*d);

b2:=arctan(sqrt(1-sqr(x1))/x1);

x2:=(1/k)*sin(f0);

b1:=arctan(x2/sqrt(1-sqr(x2)));

w1:=(b*k*sin(b1+b2)*w)/(a*a*sin(b2));

Writeln('a1= ', a1:6:3,' a2= ',a2:6:3);

Writeln('f1= ', f1:6:3,' f2= ',f2:6:3);

Writeln('w1= ',w1:6:3);

Readln;

End .