 |
Главная |
Метод обращения матрицы
|
из
5.00
|
Содержание
1. Метод последовательных приближений
2. Метод Гаусса-Зейделя
3. Метод обращения матрицы
4. Триангуляция матрицы
5. Метод Халецкого
6. Метод квадратного корня
Литература
Метод последовательных приближений
Наиболее распространенными методами применительно к большим системам являются итерационные методы, использующие разложение матрицы на сумму матриц, и итерационные методы, использующие факторизацию матрицы, т.е. представление в виде произведения матриц.
Простая итерация: уравнение  приводится к виду
приводится к виду  , например, следующим образом:
, например, следующим образом:
 ,
,
где 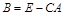 и
и  содержат произвольную матрицу коэффициентов, по возможности желательно близкую к
содержат произвольную матрицу коэффициентов, по возможности желательно близкую к  .
.
Если выбрать A=H+Q так, чтобы у положительно определенной H легко находилась  , тогда исходная система приводится к следующему удобному для итераций виду:
, тогда исходная система приводится к следующему удобному для итераций виду:
 .
.
В этом случае, при симметричной матрице A и положительно определенной Q итерационный процесс сходится при любом начальном  .
.
Если взять H в виде диагональной матрицы D= 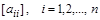 , в которой лишь на главной диагонали расположены ненулевые компоненты, то этот частный случай называется итерационным методом Якоби.
, в которой лишь на главной диагонали расположены ненулевые компоненты, то этот частный случай называется итерационным методом Якоби.
Метод Гаусса-Зейделя
Метод Гаусса-Зейделя отличается тем, что исходная матрица представляется суммой трех матриц:
 .
.
Подстановка в  и несложные эквивалентные преобразования приводят к следующей итерационной процедуре:
и несложные эквивалентные преобразования приводят к следующей итерационной процедуре:
 .
.
Различают две модификации: одновременную подстановку и последовательную. В первой модификации очередная подстановка выполняется тогда, когда будут вычислены все компоненты нового вектора. Во второй модификации очередная подстановка вектора выполняется в тот момент, когда будет вычислена очередная компонента текущего вектора. В векторно-матричной форме записи последовательная подстановка метода Гаусса-Зейделя выглядит так:
 .
.
Вторая форма требует существенно меньшее число итераций.
Метод обращения матрицы
Эквивалентные преобразования матрицы в произведение более простых, приводящих к решению или облегчающих его получение, начнем с рассмотрения метода обращения матрицы. Так как в общем виде решение системы представляется через обратную матрицу в виде  , то предположим, что
, то предположим, что
 ,
,
тогда, умножив справа равенство на матрицу A , получим
 .
.
Отсюда можно сделать вывод, что матрицы  должны последовательно сводить матрицу A к единичной. Если преобразующую матрицу выбрать так, чтобы только один ее столбец отличался от единичных векторов-столбцов, т.е.
должны последовательно сводить матрицу A к единичной. Если преобразующую матрицу выбрать так, чтобы только один ее столбец отличался от единичных векторов-столбцов, т.е.  , то вектор-столбец
, то вектор-столбец  можно сформировать таким, чтобы при умножении на текущую преобразуемую матрицу
можно сформировать таким, чтобы при умножении на текущую преобразуемую матрицу  в последней i-тый столбец превратился в единичный
в последней i-тый столбец превратился в единичный 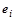 . Для этого берут
. Для этого берут
 и тогда
и тогда  .
.
Фактически это матричное произведение преобразует все компоненты промежуточной матрицы по формулам, применяемым в методе исключения Гаусса. Особенность этого процесса заключается в том, что диагональные элементы исходной и всех промежуточных матриц не должны быть нулевыми.
Кроме обратной матрицы, равной произведению всех T-матриц, теперь можно получать и решения уравнений для любого вектора в правой части.
Триангуляция матрицы
Разложение исходной матрицы на произведение двух треугольных матриц (триангуляция матрицы) не является однозначной. В соответствии с этим имеется несколько различных методов, привлекательных с той или иной стороны.
Сам способ формирования уравнений или формул для вычисления элементов треугольных матриц в различных методах практически одинаков: это метод неопределенных коэффициентов.
Различия возникают на стадии выбора условий разрешения полученных уравнений. Пусть
 ,
,
где  –
–
нижняя треугольная матрица,
 –
–
верхняя треугольная матрица.
Выполняя перемножения треугольных матриц и приравнивая получающиеся элементы соответствующим элементам исходной матрицы несложно для k-той строки и m-того столбца записать
 .
.
Полученная система состоит из  уравнений и содержит
уравнений и содержит  неизвестных коэффициентов. За счет лишних n неизвестных существует свобода выбора, благодаря которой и имеется разнообразие методов разложения.
неизвестных коэффициентов. За счет лишних n неизвестных существует свобода выбора, благодаря которой и имеется разнообразие методов разложения.
Метод Халецкого
Если положить  , то разложение и последующее решение системы из двух векторно-матричных уравнений с треугольными матрицами называется методом Халецкого.
, то разложение и последующее решение системы из двух векторно-матричных уравнений с треугольными матрицами называется методом Халецкого.
Элементы треугольных матриц L и U последовательно будут вычисляться по следующим формулам:
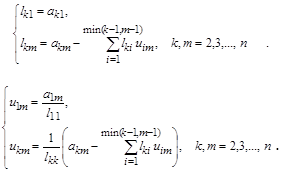
Если исходная матрица симметричная, то от треугольных матриц можно потребовать, чтобы они были друг к другу транспонированными, т.е., например,  и
и  так, что
так, что  . В этом случае элементы треугольных матриц находятся в соотношении
. В этом случае элементы треугольных матриц находятся в соотношении 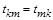 и, следовательно, число неизвестных уменьшается вдвое. В результате элементы треугольной матрицы могут вычисляться по следующим формулам:
и, следовательно, число неизвестных уменьшается вдвое. В результате элементы треугольной матрицы могут вычисляться по следующим формулам:

|
из
5.00
|
Обсуждение в статье: Метод обращения матрицы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

